2.Понятие опр.Интег-ла.
Пусть
задана ф. у=f(x)
на [a,b].
Разобьем [a,b]
произв. образом на n
частей Т: а=х0<x1<…хi<xi+1<..<xn=b,
i=1,n.
Обозн. ч\з =maxxi,
xi
= xi+1-xi.
На каждом отрезке выберем произв.
т.i[xi-1,xi.
Составим сумму:
и назовем ее интегральной
суммой на
[a,b]
ф. f.
Е\и
сущ-т I=
(>0) (>0) (<|-|<)
Он
назыв. определенным интегралом от ф-и
по dx
на [a,b],т.е.
.
Числа a,
b
наз. соответственно нижним
и верхним
пределом интегрирования.
3.Суммы Дарбу.
Пусть f огранич. на [a,b]. Рассм-м разбиение а=х0<x1<..хi<xi+1<..<xn=b
Т.к
f-огран,то
f
огран и на частичном [xi,xi+1-это
означ,что сущ-ют m,M,
что mi≤f(x)≤Mi
доможим на Δхi
и просуммируем, получ. Нижнюю сумму
Дарбу s=
mi
Δхi
и верх. сумму Дарбу S=
Mi
Δхi,
s≤σ≤S.
Св-ва:1)При добавлении новых делящих точек нижняя сумма может увеличиться,а верхняя только уменьшится.2)Любая нижняя сумма не превосхидит любую верхнюю.
4.Необх и дост усл суш-ния:Т:для сущест-ния определенного интеграла,необх и дост,чтобы lim(S-s)=0 при →0.
5.Интегр-ть непрерыв.ф-и:Т:е\и ф-я непрерывна на [a,b],то она интегрируема на нем.
Док-во:f-непрер. на [a,b] по т.Кантера(всякая ф-я непрер на [a,b] равномернонепрер на нем) f-равномернонепрер. значит (>0)(Δхi<δ→ Mi- mi<).
S-s=
Mi
Δхi-
mi
Δхi=
(
Mi-
mi)
Δхi
=
Δхi=(b-a)
след-но lim(S-s)=0,т.е.
ф-я f-интегрир
на [a,b].ЧТД
6.Св-ва опр.интегр.
1)
.
2)
Д-во:
3)
4)Если ф. f интегр-ма на [a,b] и при этом f(x)≥0, тоa∫bf(x)dx≥0.
5) Если f и g интегр-мы на [a,b] и f(x)≤g(x) на [a,b], то a∫ b f(x)dx≤ a∫ b g(x)dx.
6) Если f интегр-ма на [a,b], то и ф. |f(x)| интегр-ма на [a,b] и при этом |a∫bf(x)dx|≤a∫b|f(x)|dx.
7) Если f интегр-ма на [a,b] и при этом m≤f(x)≤M, то m(b-a) ≤ a∫ b f(x)dx ≤M(b-a).
8)(Т. о среднем) Если ф. f интегр. на [a,b] и m≤f(x)≤M,то сущ-ет μ,что a∫ b f(x)dx = μ(b-a).
7.Опр.Инт.С переменным верх.Приделом.
х[a,b]
по св-ву 3 сущ-ет опр-ный интеграл. Поставим
каждому такому х в соотв-е знач-е
φ(х)=
св-ва:1)е\и f-интегрируема на [a,b], то φ-непрерыв в любой точке отрезка. 2)е\и f-непрерыв на [a,b], то φ-диф-ма и φ’(x)=f(x). 8.Формула Ньютона-Лейбница: если ф-ия f непрерывна на a,b и F одна из ее первообразных, то ab f(x)dx=F(b)-F(a). Док-во: a∫ х f(t)dt=F(x)+C. Положим х=а, след. 0=F(a)+C, тогда С=-F(a) след. a∫ х f(t)dt=F(x)-F(a). Положим х=b, тогда a∫ b f(t)dt=F(b)-F(a).Δ Для удобст.a∫ b f(х)dх = F(x)|ab=F(b)-F(a).
Вычисление площадей плоских фигур
пусть
кривол. трапеция с основаниями a,
b
и ограниченной сверху графиком непрерывной
и неотрицательной на [a,
b]
функцией y=f(x),
тогда площадь:
.
Если кривол. трап. ограничена снизу и
сверху кривыми:
и
,
(a≤x≤b),
то
.
Пр: Вычислить S фигуры огран. y=cosx,Ох и Оу.
S=
1
Объем
тела вращения:
,
если
криволинейная трапеция, ограниченная
кривой y=f(x)
и прямыми y=0,
x=a,
x=b,
вращается вокруг оси Ox.
Длина
дуги: а)
если кривая
задана парамет-рическими уравнениями
,
то
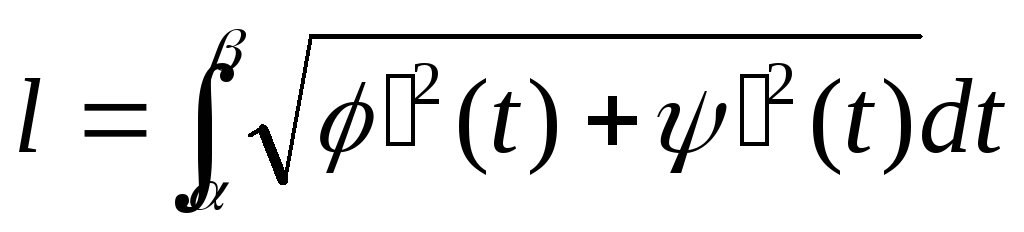.б)
если кривая
задана в явной форме y=f(x),
,
то
.
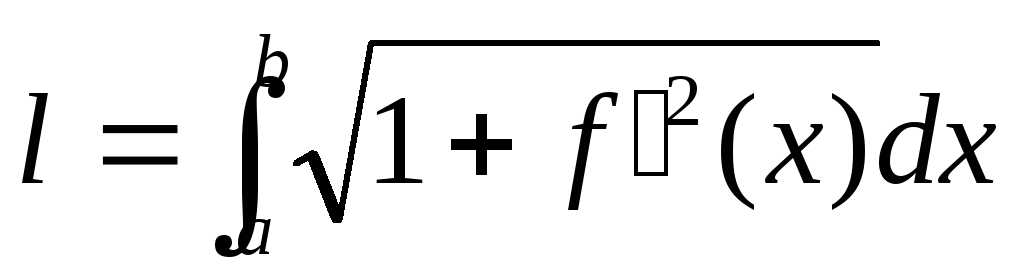М2 – 6 Числовые ряды (Ч.р.). Признаки сход-ти. Абсол-я и условная сход-ть.
Опр.
Пусть дана числ-я послед-ть (an),
символ вида
(1)
наз-ся числовым
рядом (ч.р.),
a1,a2,…an,..
- члены ч.р. (1), an
– общий член ряда (1).
Опр.
Если посл-ть част-х сумм числового ряда
(1) имеет конечный предел
,
то ряд (1) наз-ся сходящимся,
число S
наз-ют суммой
ряда (1) и
пишут
.
Если предел послед-ти част-ых сумм не
сущ-ет или бесконечен, то говорят, что
ряд (1) расходится.
пример
Т.
Необх-й признак
сход-ти: Если
ч.р.
(1) сходится, то его общий член → к 0 при
неограниченном возраст-нии его номера
.
Следствие:
Если
или не сущ-ет, то ряд (1) расходится.
Зам:
Утвержд-е обратное Т. неверно: если
,
ряд (1) м/б как сход-ся, так и расход-ся.
Т. Необх.и дост.усл.сходимости полож.рядов. Д.т.ч. ряд с положительными членами сх-ся, необх.и дост., чтобы посл-ть (Sn), его частичных сумм была ограничена сверху.
Т.
Признак Даламбера:
Пусть для ч.р.
(1),
и
.
Если
,
то ряд (1) сходится, если q>1,
то ряд (1) - расходится.
Док-во:
1)
Пусть
,
.
Зададим
т.ч.
.
(по
опр. предела). По св-ву модуля:
Пусть
.
Рассм.правую часть посл.нер-ва: при
(т.к. ряд положит.)
при
и.т.д.
.
Получили члены ряда
членов
ряда
(сходится),
тогда и получ.ряд сх-ся как геом.ряд со
знаменателем
.
2).
Пусть
,
.
Выберем
т.ч.
.
Из нер-ва
.
при
при
и.т.д.
.
члены
ряда
членов
ряда
(расходится),
тогда и получ.ряд сх-ся как геом.ряд со
знаменателем
.
расх.по
1 приз., а он явл.ост. исх.ряда,значит, он
тоже расх. ■
Зам: Если q=1, то пр-к Даламбера не дает ответ на вопрос о сход-ти или расход-ти ряда. Следует использовать другие признаки.
Пример:
Исследовать на сход-ть:
.
1)
,
;
2)
,
→
(по пр-ку Даламбера) ряд сходится. ■
Т.Радикальный
признак Коши:
Пусть для ч.р.
(1)
и
.
Если
,
то ряд(1) сходится, если q>1,
то ряд (1)- расходится.
Зам: Если q=1, то пр-к Коши не применим. Следует исп-ть др-е пр-ки
Т.
Интегральный
признак Коши-Маклорена:
Если ф-ция y=f(x)
– непрерывна, неотриц-на и не возрастает
на
.
Если
сходится, то ряд
(1)
сходится, если
расходится,
то ряд(1) расходится.
Опр. Ч.р., у к-го 2 любых соседних члена имеют разные знаки наз-ся знакочер-ся.
Т. Лейбница: Если члены знакочер-ся ряда убывают по абсолютной величине и общий член стремится к нулю при n→∞, то ряд сходится.
Док-во:
Пусть
ряд
т.ч.
выполн. 2 условия:
1.
2.
.
1.
Док-ем, что ряд сх-ся. Рассм. четное число
членов:
(из
1 условия)
Итак,
можно представить
Док-ли,
что
-положит.,
возр., и огр.сверху, след-но,
-сх-ся.
2.
Рассм.посл-ть нечет.частич. сумм ряда
(2-ой предел=0 из 2-го условия)-след-но, ряд сх-ся. ■
Н-р: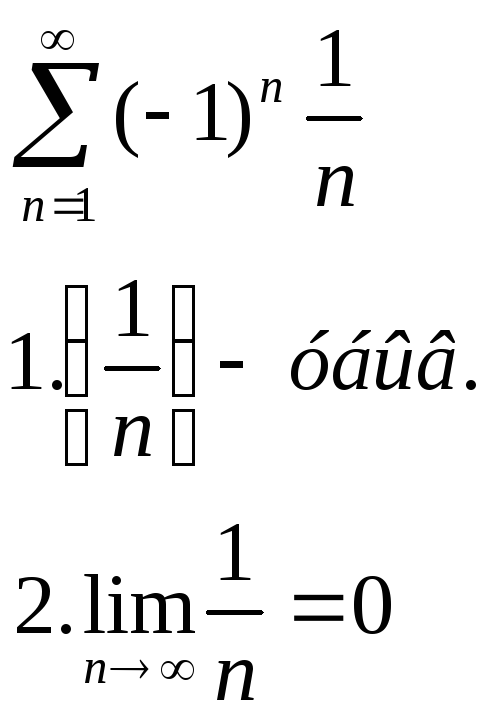
исх.ряд
сх-ся
Опр.
Если для
ряд
- сходится, то говорят, что ряд
сходится
абсолютно.
Опр.Если
сходится,
а
расход-ся, то говорят, что ряд
сходится
условно
(неабсолютно).
М2 - 7 Степенные ряды. Ф-ла и ряд Тейлора. Разложение элем-ых ф-ий в ряд Тейлора.
Опр.
Функц. ряд (1)
,
где x0,
cn
(n=0,1,..)
–действ. числа, наз-ся степ.
рядом по степеням (x-x0).
Ряд
(1) заменой y=x-x0
можно свести к ряду (2)
.
Степ. ряд вида (1) сходится в т. x=0.
Н-р:
по
рад-му признаку расх-ся всюду, сх-ся
только в т.x=0
Т.
Абеля.
Если ст. ряд сх-ся в т.
,
то он абсолютно сх-ся в любой точке x,
удовлетворяющей условию |x|<|x1,
если ряд расходится в т. х2,
то он расходится в любой точке х, удовл-щей
усл-ю |x|>|x2|.
Док-во:
-
сх-ся => (по необх. признаку сход-ти
чис. ряда)
,
значит по свойству предела чис. послед-ти
. Пусть x
– фиксир-е действ-е число т.ч.,
.
Тогда
.
Ряд
-
сх-ся, т.к. составлен из членов бесконечно
убывающей геом. прогрессии (по усл
).
След-но,
сх-ся (по 1 признаку сравн-я)=>
(по св-ву сх. рядов)=>
сх-ся
абсолютно.
В силу произв-ти выбора x ст. ряд явл-ся абс. сх-ся при всех x, для к-рых |x|<|x1|.
интервал и радиус сход. степ. ряда.
Теор.: для всякого сход. степ. рядаn=0anxn (1) хотябы в одной т. х0, сущ. Такой интервал (-R; R) что ряд сход. абсолютно во всякой внутр-енней т. и расход. во всякой внешней точке этого интервала.
Опр.: (-R;R) наз. интервалом сход. ряда(1), R наз радиусом сход. этого ряда.
Н-р:
Исследуем на абс-ую сх-ть ряд
.
Этот ряд будет сх-ся при
При
х=-3 ряд расх-ся. При х=1 ряд расх-ся. Итак,
область сх-ти ряда (1,3)
равн-ная сход. степ. ряда.
Теор.: степ. ряд n=1cnxn (1) с радиусом сход. r равн-но сход. В каж.[-r,r1], где r1<r.
непр-ность суммы степ. ряда.
Теор.: сумма степ. ряда есть ф-ия непр-ная внутри интервала сход.
Док-во: пусть х(-R; R), очевидно, что можно выбрать такое r>0, что
–R<-r<x<r<R по теор. О равн-ной сход. степ. ряда ряд сход. равн-но. Члены ряда Un(x)=an*x^n непр-на как степ. ф-ия на основании теор. Непр-ности суммы ряда непр-на на [-r;r], а след. Непр-на в т.х т.к. точка произвольная, то непр-на во всякой точке[-r;r].
задача разложения ф-ии в степ. ряд. единственность разложения.
Из
теор.о почленном диф-ии степ.ряда (Теор.:
степ. ряд
anxn
внутри его
промежутка сход. можно почленно диф-ть,
если S
его сумма, тоS(x)
непр-но диф-ма и справедливо равенство
S’(x)=
n=0nanxn-1
(2))следует
речь о ф-ии f
в степ.ряд можно ввести в случае если
эта ф-ия имеет производную всех порядков
в некотрм интервале в этом случае
говорят, что f
явл. Бесконечно диф-ной.
Теор.: если ф-ия f в (x0-R;x0+R) разлагается в степ. Ряд
an*(x-х0)n
,то лишь
единствным образом.
Опр.:
рядом
Тейлора
бесконечно
диф-нойф-ии f(x)
в т. х0
наз. степ. Ряд вида
*(х-х0)
(n)
Формула Тейлора для многочлена:
Условие разложения ф-ии в ряд Т-а
Т1.
Д.т.ч.ряд Т-а ф-ии f,
построен-ый в
сх-ся к ней в этом инт-ле необх и дост.,
чтобы ост.член ф-лы Т-а→0 при n→
при всех
Т2. Е\и ф-ия f беск-но дифф-ма на [a,x] и все ее произ-ые огр-ны одним и тем же числом, то ряд Т-а для ф-ииf сх-ся к ф-ии f в [a,x].
применение формулы Тейлора к разложению некоторых элементарных ф-ий.
1)
,
1. f’(x)=ex; f’’(x)=ex;…, f(n)(x)=ex
2. Пусть x=0, . f(0)=1; f’(0)=1;…, f(n)(0)=1.
3.
4. Зафиксир-ем нек-рые х. По признаку Даламбера найдем интервал сходимости ряда
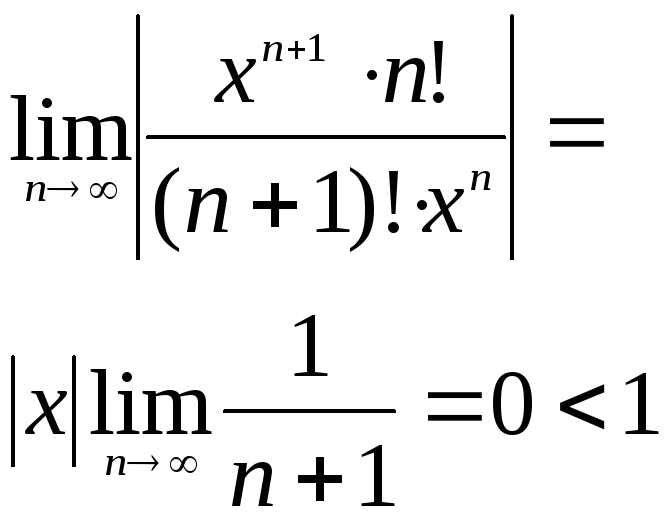
Сходится на (-∞;+∞), где х – фиксир-е число.
5. Зафиксир-ем нек-рое h>0, такое что |x|<h, тогда имеет место нер-во ex=eh, а значит построенный ряд сходится в инт-ле (-h;h). В силу того, что h можно выбрать достаточно большим, построенный ряд сходится к ф-ции y=ex на (-∞;+∞).
Итак
Пример:
-
y=sin(x), D(y)=
-
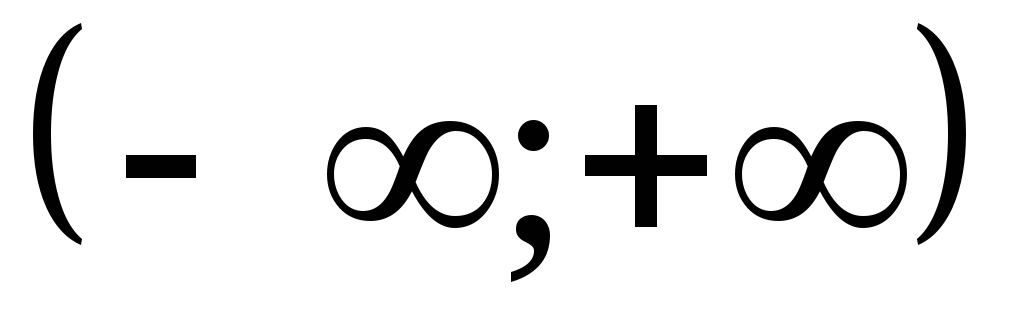
y=cos x, D(y)=R.
-
y=ln(1+x), D(y)=(-1;+∞);
,
-
y=(1+x)α,
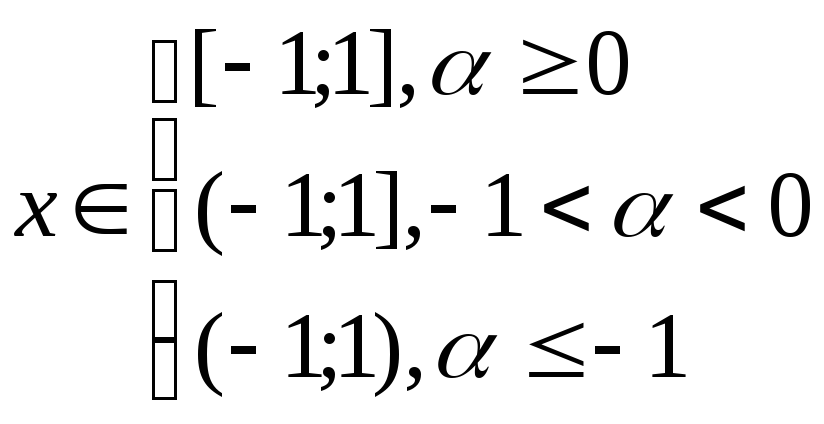
2) f(x)=sinx
рассмотрим [-H;H], где H-произвольное
f(n) (x)=sin(x+n*П/2)
| sin(x)|=| sin(x+n*П/2)| ≤1 имеет место разложение в ряд Тейлора на [-H;H], т.к. H-произвольное то имеет место разложение на R
sinx=x-x3/3!+…+
(-1)nx2n-1/(2n-1)!+…=
(-1)n
*x2n-1/(2n-1)!
; x
R.
-
f(x)=cosx
Cosx=1-
x2/2!+x4/4!
–x6/6!+…+(-1)n*
x2n/(2n)!+…=
(-1)n*
x2n/(2n)!
; x
R.
4) f(x)=ln(1+x), x>-1
Ln(1+x)= x-x2/2+x3/3+…+ (-1)n-1 (x)n/ n+…, где |x|<1
5)
в
(-1;1)