42

Глава 3. Стационарные магнитные поля в электрических машинах

3.1. Магнитное поле индукторов бесконечно длинных индукционных машин

3.1.1. Общая характеристика магнитного поля в зазоре

Предварительные замечания. Магнитное поле индуктора МГД-машин, создаваемое обмоткой индуктора, можно называть также первичным магнитным полем.

Как уже указывалось, рассматриваются многофазные индукционные МГД-машины. Первичное магнитное поле в немагнитном зазоре между сердечниками индуктора этих машин имеет такой же характер, как и в обычных многофазных электрических машинах, и эта общность заключается прежде всего в наличии бегущего магнитного поля. Однако в линейных индукционных машинах, плоских и цилиндрических, вследствие конечной длины сердечников в первичном магнитном поле возникают также добавочные, неподвижные в пространстве и пульсирующие во времени составляющие магнитного поля. Явление возникновения этих полей называют также краевыми эффектами. Поскольку в линейных машинах сердечники индуктора не свернуты в замкнутое кольцо, как в нормальных электрических машинах, и поэтому магнитная цепь линейных машин на своих концах разомкнута, эти машины часто называют также машинами с разомкнутым магнитопроводом. Соответственно говорят также, что краевые эффекты, или появление пульсирующих полей, обусловлены разомкнутостью магнитопровода линейных машин.

Кроме того, вследствие большой величины зазора в МГД-машинах магнитная индукция в зазоре по направлению от одного сердечника к другому изменяется в них гораздо сильнее, чем в обычных электрических машинах. По этим причинам магнитное поле в зазоре индукционных машин необходимо рассмотреть отдельно. Некоторые особенности имеют также магнитные поля рассеяния индукционных МГД-машин. Прежде всего, рассмотрим магнитное поле в зазоре бесконечно длинной плоской линейной машины, когда краевые эффекты не проявляются. Так как в винтовых индукционных МГД-машинах и в обычных электрических машинах величина зазора по сравнению с радиусом обычно мала, то получаемые результаты с большой точностью применимы также к обычным электрическим машинам.

Характер поля в зазоре и упрощение задачи. В электрических и МГД-машинах катушки обмоток укладываются в пазах. На рисунке 3.1,а изображен индуктор с тремя пазами на полюсное деление, и на каждом сердечнике показано распределение токов в пазах на протяжении для некоторого момента времени.

Под влиянием пазов магнитное поле в зазоре приобретает весьма сложный характер и трудно поддается расчету. Поэтому обычно принимают (рис.3.1,б), что поверхности индукторов лишены пазов и на них расположены бесконечно тонкие токовые слои или поверхностные токи, линейная плотность которых находится в определенном соответствии с реальной токовой нагрузкой обмоток. Для упрощения задачи принимают также, что для стали сердечников и машина имеет в направлении оси (рис. 3.1) бесконечные размеры, т. е. рассматривают плоскопараллельную задачу, когда . Влияние принятых допущений может быть с той или иной точностью учтено впоследствии дополнительно.

Напряженность магнитного поля в зазоре индуктора по рис. 3.1,б при принятых допущениях имеет две составляющие: и , из которых наибольшее значение для основных рабочих процессов в машине имеет составляющая . Учет обеих составляющих поля и изменения величины по координате на рис.3.1,б вызывает определенное усложнение математических соотношений и связанных с ними расчетов, хотя на численные результаты указанные факторы в большинстве случаев влияют мало. Поэтому в теории электрических машин обычно принимается, что не только , но также и вдоль координаты постоянна. Соответственно при бегущем вдоль координаты поле принимается, что

(3.1)

где .

Необходимо отметить, что подобного бегущего магнитного поля в действительности существовать не может, так как при этом не соблюдается уравнение Максвелла (1.1). Действительно, вычислим проекции для некоторой точки зазора (рис. 3.1, а или б).

Если иопределяется равенством (3.1), то

(3.2)

.

Таким образом, , хотя плотность тока в зазоре равна нулю, и поэтому при может существовать только в случае, когда на протяжении всего зазора ток распределен с определенной плотностью:

.

Рис. 3-1. Характер магнитного поля в зазоре при распределении обмотки в пазах сердечников (а), на гладких поверхностях сердечников (б), в зазоре между сердечниками (в)

Согласно (3.1)

. (3.3)

Таким образом, приходим к выводу, что при дальнейшей идеализации задачи, когда существует только первичное поле по (3.1), необходимо принять, что ток обмотки сосредоточен не в пазах (рис. 3.1, а) и не на поверхностях индуктора (рис. 3.1,6), а распределен равномерно по сечению зазора величиной (рис. 3.1, в). При этом объемная плотность токав соответствии с (3.3) должна представлять бегущую волну. В связи с этим можно представить себе, что обмотка вынесена из пазов и рассыпана в виде бесконечно тонких проводников по всему сечению зазора, а сами пазы заполнены сталью.

Хотя в теории электрических машин обычно и принимается, что поле в зазоре изменяется согласно (3.1), связанные с этим изложенные выше соображения не приводятся.

Реальная обмотка создает, кроме основной гармоники поля, определяемого (3.1), также высшие гармоники поля. Тогда необходимо представить себе, что в зазоре наряду с основной гармоникой объемной плотности тока по (3.4) существуют также высшие гармоники плотности тока.

3.1.2. Магнитное поле плоского линейного индуктора с токовыми слоями на поверхностях сердечников.

Общее решение. Индуктор рассматриваемого вида изображен на рис. 3.1,б. При расчете первичного поля можно принять, что зазор заполнен воздухом, для которого игн/м.

В случае рис. 3.1,б сторонних токов в зазоре нет, и поэтому также . Кроме того, и , от координаты не зависят. При этих условиях уравнения Лапласа приобретают вид:

В данном случае среду зазора можно считать неподвижной (), но использование этого условия в силу не требуется.

При решении исследуемой задачи необходимо также знать граничные условия для и на поверхностях раздела рассматриваемой области с внешним пространством. Такими поверхностями на рис. 3.2,б являются поверхности .

Рис. 3.2. Установление условий для напряженности магнитного поля при наличии поверхностных токов

По принятым выше условиям при и имеем . При этих условиях и при отсутствии на поверхностях поверхностных токов магнитные линии были бы перпендикулярны к этим поверхностям, и тогда эти граничные условия имели бы вид:

(3.4)

где величина определяется намагничивающей силой (н.с.) обмоток индуктора. Однако в рассматриваемом случае (рис. 3.2,б) на поверхностях имеются поверхностные токи, и поэтому граничные условия являются другими.

Допустим для общности задачи, что величины поверхностных токов на поверхностях различны. Мы рассматриваем случай синусоидального бегущего поля, когда линейные токовые нагрузки и рассматриваемые поверхностные токи также представляют собой синусоидальные бегущие волны. Тогда линейная плотность тока на верхней поверхности индуктора (при ):

и на нижней поверхности ()

или в комплексной форме

(3.5)

Здесь и – амплитуды линейных плотностей токов, которые выражаются через обмоточные данные и токи обмоток так, как будет показано ниже.

Выделим на пограничных поверхностях (рис. 3.1,б) участки бесконечно малой длины, как показано на рис. 3.2, и применим для этих участков закон полного тока

, (3.6)

Полагая, что участки прямоугольных контуров интегрирования длиной расположены вплотную к пограничным поверхностям с обеих сторон и поэтому длины поперечных участков этих контуров равны нулю. Поскольку для стали сердечников принято , то напряженность поля в стали. Поэтому вместо (3.6) получим для рис. 3.2, а:

и для рис. 3.2,б:

или на основании (3.5):

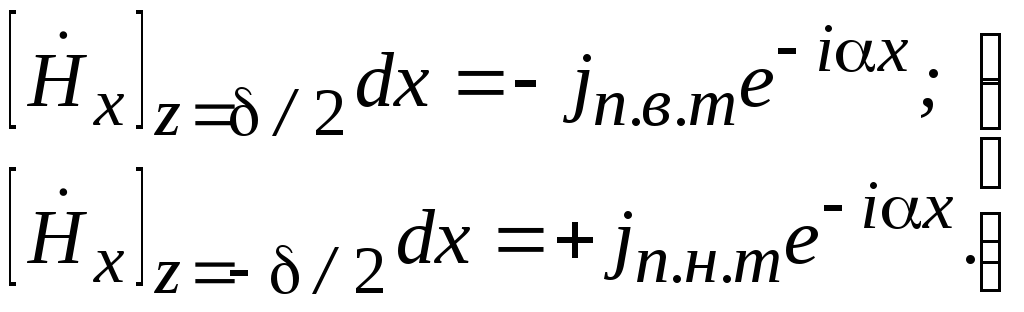(3.7)

Таким образом, при рассматриваемых условиях составляющие , касательные к граничным поверхностям, равнылинейным плотностям поверхностных токов в данной точке. Этот факт известен также из книг по физике и электротехнике.

Граничные условия составляющих получим из условия:

что в рассматриваемом случае дает

Подставив сюда значения по (3.7) в качестве граничных условий, для получим:

(3.8)

Так как рассматриваемое магнитное поле создается синусоидальными бегущими волнами тока, то и оно представляет собой синусоидальную бегущую волну. Поэтому решения уравнений поля можно искать в виде:

или в комплексной форме:

(3.9)

где ,,,– вещественные и комплексные амплитуды составляющих напряженности поля, зависящие только от координаты .

Подставив и по (3.9) в (3.4) и сократив все члены уравнений на , получим уравнения для определения и :

(3.10)

Решения этих уравнений имеют вид:

(3.11)

где , , , – постоянные интегрирования.

В правильности этих решений можно убедиться подстановкой их в (3.10).

Согласно (3.7) и (3.9):

(3.12)

Полагая в первом уравнении (3.11) поочередно и и подставляя соответствующие этим координатам значения по (3.12), получаем уравнения для определения постоянных интегрирования:

Из этих уравнений находим:

и, следовательно, согласно (3.11)

(3.13)

Продифференцируем соотношения (3.9) для пои подставим затем поочередно значения производныхпо (3.8). Тогда получим граничные условия для:

(3.14)

Теперь продифференцируем второе уравнение (3.11) по и подставим затем поочередно и и значения соответствующих производных по (3.14).Тогда получим уравнения для определения постоянных интегрирования:

Из этих уравнений находим:

и, следовательно, согласно (3.11)

(3.15)

Этим решение уравнений Лапласа заканчивается, и остается рассмотреть несколько практически важных частных случаев.

Индуктор с двусторонней обмоткой. Обычно на обоих сердечниках индуктора плоской линейной машины размещаются идентичные обмотки, которые питаются одинаковыми токами. Тогда

(3.16)

и равенства (3.13) и (3.15) упрощаются. Выразим сначала ичерез рассматриваемую в теории электрических машин линейную токовую нагрузку , которая представляет собой величину действующего значения тока обмотки на единицу его длины:

, (3.17)

где – число фаз обмотки;– число последовательно соединенных витков фазы обмотки или число витков одной еепараллельной ветви; – действующее значение тока фазы обмотки, равное суммарному току всех ее параллельных ветвей; – число пар полюсов;– полюсное деление.

Здесь и ниже будем рассматривать обмотки двух сердечников как единую обмотку. При этом – полный ток фазы индуктора, а в случае последовательного соединения витков в обмотках обоих сердечников и последовательного соединения этих обмоток; – полное число витков всего индуктора.

Таким образом, по (3.17) – суммарная линейная нагрузка обоих индукторов.

Установим также связь между и амплитудой основнойгармоники н. с. обмотки при ее симметричной нагрузке. Как известно,

, (3.18)

где – обмоточный коэффициент для основной гармоники.На основании (3.17) и (3.18)

. (3.19)

На рис. 3.3 изображена синусоидальная волна поверхностного тока:

, (3.20)

Рис. 3.3. Синусоидальные волны поверхностных токов или линейной токовой нагрузки и намагничивающей силы

Как известно, кривая н. с. представляет собой интеграл кривой распределения тока. Поэтому

, (3.21)

или

.

На основании (3.19) и (3.21)

. (3.22)

Согласно (3.22) амплитуда линейной плотности тока индуктора представляет собой амплитуду линейной нагрузки обмотки, что вполне естественно. Множитель входитв (3.22) потому, что в соответствии с (3.17) вычисляется по действующему значению тока, а умножение на выделяет основную гармонику.

Равенство (3.22) выражает суммарную линейную плотность тока обмотки обоих индукторов через общеизвестные из теории электрических машин величины и.

Мы можем принять и за вещественные числа. Тогда согласно (3.16) на основании изложенного

(3.23)

где определяется по равенству (3.22).

Из (3.13), (3.15), (3.22) и (3.23) в случае двусторонней обмотки находим

(3.24)

В середине зазора, при , для модулей и имеем:

(3.25)

причем принято обозначение .

Напряженность поля в середине зазора и соответствующая ей индукция представляет интерес в связи с тем, что плоскость совпадает с серединой слоя жидкого металла.

На рис. 3.4, а изображены зависимости и от , т. е. вдоль длины зазора для рассматриваемого случая.

Рис. 3.4. Распределение составляющих напряженности магнитного поля по ширине зазора плоских линейных индукторов:

а – двухсердечниковый индуктор с двусторонней обмоткой; б – двухсердечниковый индуктор с односторонней обмоткой; в – односердечниковый индуктор

Коэффициент

(3.26)

определяет степень ослабления -й компоненты поля в середине зазора по сравнению с ее значением на поверхностях сердечников. Согласно (3.2) и (3.24) - (3.26)

. (3.27)

Значения по (3.27) представлены на рис. 3.5 в виде кривой 1.

Рис. 3.5. Кривые коэффициентов идляплоских

линейных индукторов

В теории электрических машин величина амплитуды н. с. определяется через магнитную индукцию в зазоре по формуле

, (3.28)

где - коэффициент зазора, учитывающий его неравномерность.

Введем подобную формулу для выражения н. с. индуктора с двусторонней обмоткой через индукцию в середине его зазора :

, (3.29)

где - коэффициент зазора, учитывающий увеличениен. с. вследствие увеличения индукции по направлению от центра зазора к поверхности сердечников.

Подставив в (3.29) по (3.25), с учетом (3.2) получим

. (3.30)

Величины по (3.30) представлены на рис. 3.5 в виде кривой 3.

Индуктор с односторонней обмоткой. Если у индуктора с двусторонней обмоткой удалить обмотку одного сердечника, то получится индуктор с односторонней обмоткой (рис. 3.6). Такие индукторы менее выгодны, так как в них при одинаковых условиях охлаждения общую линейную нагрузку обмотки необходимо снижать вдвое и поле в зазоре также ослабляется приблизительно вдвое. Тем не менее, такие индукторы могут находить некоторое применение. Кроме того, этому случаю соответствует и первичное поле нормальных неявнополюсных электрических машин переменного тока, так как в них первичная обмотка расположена на одном из сердечников.

В рассматриваемом случае в (3.13) и (3.15) в соответствии с рис. 3.6 необходимо положить

причем и здесь определяется равенством (3.22), и сохраняют силу также равенства (3.18) - (3.21).

Рис. 3.6. Магнитное поле плоского линейного индуктора с односторонней обмоткой

Кроме того, в соответствии с рис. 3.6 начало координат перенесем на поверхность нижнего сердечника, и поэтому в (3.13) и (3.15) необходимо заменить на . Тогда вместо (3.13) и (3.15)получим

(3.31)

Согласно (3.31) при

а при

В середине зазора () на основании (3.31)

(3.32)

Полученные граничные значения вполне согласуются с элементарными физическими соображениями, относящимися к случаю рис. 3.6. Характер изменения и вдоль координаты показан на рис. 3.4, б.

В рассматриваемом случае обозначим

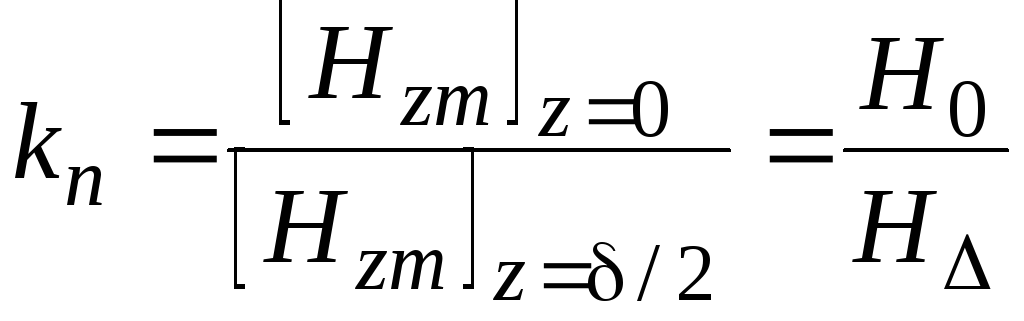. (3.33)

Тогда согласно полученным соотношениям

(3.34)

Значения по (3.34) представлены на рис. 3.5 в виде кривой 2.

Подставив в правую часть (3.29) сначала значение по(3.32), а затем значение из (3.21), получим значение дополнительного коэффициента зазора для рассматриваемого случая:

(3.35)

Значения по (3.35) совпадают с их значениями по (3.30) и поэтому также изображаются кривой 2 на рис. 3.5

Односердечниковый индуктор. Если у двухсердечннкового индуктора (рис. 3.6) удалить сердечник без обмотки, то получится односердечниковый индуктор (рис. 3.7). Односердечниковые индукторы применяются в электромагнитных перемешивателях жидких металлов и в индукционных желобах. Чтобы найти выражения для и , в рассматриваемом случае, произведем сначала в числителях дробей равенств (3.31) замену гиперболических функций по формулам:

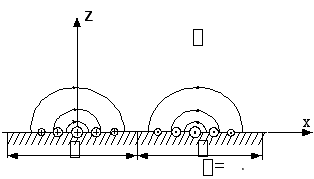
Рис. 3.7. Магнитное поле односердечникового индуктора

Затем перейдем к пределу , что соответствуетудалению верхнего сердечника индуктора (рис. 3.6) на бесконечность, и примем во внимание, что