1. Выполнение пп.1-3 задания в командном окне matlab.

Смоделируем низкочастотный гармонический сигнал частота сигналаf=2Гц. Для получения модулированного сигнала будем использовать формулу (10):

(10)

где - частота несущего колебания.

Получим модулированный сигнал для различных значений глубины модуляции

Построим исходный и модулированный сигнал, а также спектр модулированного сигнала

2. Выполнение п.4 задания в командном окне matlab.

Для выполнения модуляции с подавлением несущей воспользуемся низкочастотным сигналом из п.1 и формулой (11):

(11)

Значения частот такие же, как и в п.1. Возьмем

Построим исходный и модулированный сигнал, а также спектр модулированного сигнала.

3. Выполнение п.5 задания в командном окне MATLAB.

Для выполнения синхронного детектирования воспользуемся исходным и модулированным сигналом из п.1, а также формулой (12):

(12)

Построим исходный сигнал, модулированный сигнал, сигнал после выполнения синхронного детектирования и его спектр.

4. Выполнение п.6 задания.

Для нахождения КПД модуляции воспользуемся формулой

(13)

0,5
1
1,5

5. Выполнение п.7 задания.

Смоделируем два низкочастотных сигнала , частота сигналовПостроить моно и разностный сигналы, используя формулы.

Задать поднесущую частоту, построить композитный сигнал и его спектр.

Для описания композитного сигнала использовать формулу

. (14)

Пример программы, выполненной в среде Matlab, приведен в Приложении 3.

5. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем заключается процесс модуляции сигнала?

2. Что такое амплитудная модуляция?

3. Какие виды АМ различают? Опишите каждый вид АМ.

4. Что такое демодуляция?

5. Опишите метод синхронного детектирования.

6. Для чего используют полярную модуляцию?

7. Что называют композитным стереосигналом?

ЛАБОРАТОРНАЯ РАБОТА №4

Угловая модуляция

1. ЦЕЛЬ РАБОТЫ

Исследование процессов угловой модуляции и демодуляции.

2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

При угловой модуляции в несущем гармоническом колебании значение амплитуды колебанийостается постоянным, а информацияпереносится либо на частоту, либо на фазовый угол.

1. Фазовая модуляция

Уравнение ФМ – сигнала определяется выражением:

(1)

где – коэффициент пропорциональности. При, ФМ – сигнал является простым гармоническим колебанием. С увеличением значенийполная фаза колебаний нарастает во времени быстрее и опережает линейное нарастание. При уменьшении значенийскорость роста полной фазы во времени спадает. В моменты экстремальных значенийабсолютное значение фазового сдвига между ФМ – сигналом и значениемнемодулированного колебания также является максимальным и носит название девиации фазы (вверх, или внизс учетом знака экстремальных значений модулирующего сигнала).

2. Частотная модуляция

ЧМ характеризуется линейной связью модулирующего сигнала с мгновенной частотой колебаний, при которой мгновенная частота колебаний образуется сложением частоты высокочастотного несущего колебания со значением амплитуды модулирующего сигнала с определенным коэффициентом пропорциональности:

. (2)

Уравнение ЧМ – сигнала:

. (3)

Аналогично ФМ, для характеристики глубины частотной модуляции используются понятия девиации частоты вверх , и вниз.

Частотная и фазовая модуляция взаимосвязаны. Если изменяется начальная фаза колебания, изменяется и мгновенная частота, и наоборот. По этой причине их и объединяют под общим названием угловой модуляции (УМ). По форме колебаний с угловой модуляцией невозможно определить, к какому виду модуляции относится данное колебание, к ФМ или ЧМ, а при достаточно гладких функциях формы сигналов ФМ и ЧМ вообще практически не отличаются.

Уравнение для фазы , где- индекс угловой модуляции (modulation index), которым задается интенсивность колебаний начальной фазы.

Полная фаза модулированного сигнала с учетом несущей частоты:

. (4)

Уравнение модулированного сигнала:

. (5)

Мгновенная частота колебаний:

. (6)

Как следует из этих формул, и начальная фаза, и мгновенная частота изменяется по гармоническому закону. Максимальное отклонение от среднего значения равно, и получило названиедевиации частоты (frequency deviation). Отсюда, индекс угловой модуляции равен отношению девиации частоты к частоте модулирующего сигнала:

(7)

Различия между частотной и фазовой модуляцией проявляются при изменении частоты модулирующего сигнала.

При фазовой модуляции девиация частоты прямо пропорциональна , а индекс угловой модуляции от частоты модулирующего сигнала не зависит:.

Напротив, при ЧМ постоянным параметром модуляции является девиация частоты, при этом индекс модуляции обратно пропорционален частоте модулирующего сигнала:

3. Спектры сигналов с угловой модуляцией.

При малых значениях индекса угловой модуляции , узкополосная модуляция) имеют место приближенные равенства:

(9)

Тогда

(10)

то есть амплитудные спектры однотональных ФМ и ЧМ сигналов при практически аналогичны АМ сигналам и также содержат верхнюю и нижнюю боковые частотыи. Различие заключается только в смене знака амплитуды нижней боковой частоты на минус. Соответственно, гармонические АМ сигналы могут быть трансформированы в ЧМ сигналы изменением на 180º начальной фазы одной из боковых полос. При малых значениях индексаосновная мощность сигнала приходится на несущую частоту. С ростом индекса модуляции полоса частот, занимаемая сигналом, расширяется. Практическая ширина спектра сигнала с угловой модуляцией определяется по формуле:. Формирование реальных сигналов, как правило, выполняется при, при этом эффективная ширина спектра равна удвоенной девиации частоты:.

4. Квадратурная модуляция

Квадратурная модуляция позволяет модулировать несущую частоту одновременно двумя сигналами путем модуляции амплитуды несущей одним сигналом, и фазы несущей другим сигналом. Уравнение результирующих колебаний амплитудно-фазовой модуляции:

(11)

Пример организации амплитудно-фазовой модуляции

f0 := 50 f1 := 2 f2 := 3 'Частоты в Гц несущей, первого и второго сигналов.

'Первый модулирующий сигнал (моногармоника с амплитудой 1).

'Первый модулирующий сигнал (моногармоника с амплитудой 1).

'Перенос информации s2_n на фазу

'Амплитудно-фазовая модуляция

Рис. 1. Временная характеристика сигналов

Спектр такого сигнала будет выглядеть следующим образом:

Рис. 2. Спектральная характеристика модулированного сигнала

Сигнал s(t) обычно формируют в несколько другой последовательности, с учетом последующей демодуляции. Раскроем косинус суммы и представим сигнал в виде суммы двух АМ-колебаний.

(12)

При и, сигналыa(t) и b(t) могут быть использованы в качестве модулирующих сигналов несущих колебаний и, сдвинутых по фазе на 90^о относительно друг друга:

'Формирование модулирующих сигналов

Рис. 3. Временная характеристика модулирующих сигналов.

Сигнал называют квадратурным (quadrature), а способ модуляции -квадратурной модуляцией (КАМ).

Спектр квадратурного сигнала может быть получен непосредственно по уравнению балансной модуляции для суммы двух сигналов:

(13)

Демодуляция квадратурного сигнала соответственно выполняется умножением на два опорных колебания, сдвинутых относительно друг друга на 90^о:

, (14)

. (15)

Низкочастотные составляющие a(t) и b(t) выделяются фильтром низких частот. Как и при балансной амплитудной модуляции, для точной демодуляции сигналов требуется точное соблюдение частоты и начальной фазы опорного колебания.

3. ЗАДАНИЕ

1. Получить ФМ-сигнал и его спектр при различных значениях коэффициента угловой модуляции.

2. Получить АФМ, квадратурный сигналы и их спектры. Произвести сравнение.

3. Провести демодуляцию квадратурного сигнала. Сравнить огибающие полученных сигналов с модулирующими сигналами. Построить спектры демодулированных сигналов.

4. ХОД РАБОТЫ

1. Смоделируем низкочастотный гармонический сигнал (, частота сигнала).

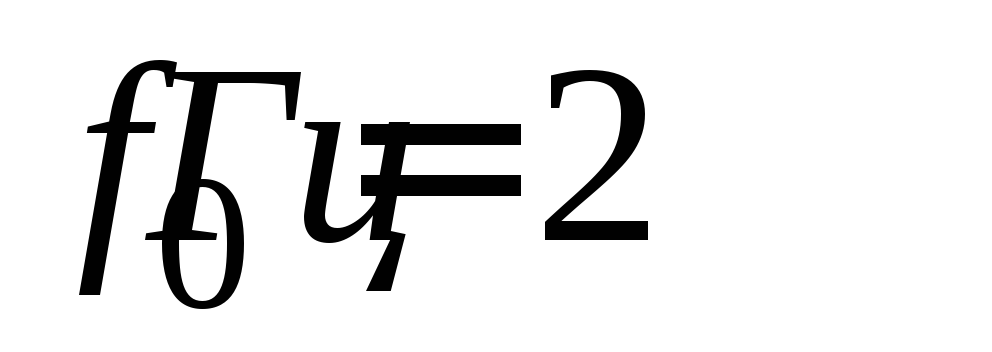Смоделируем высокочастотный несущий сигнал .

Получим модулированный сигнал для различных значений индекса угловой модуляции. Построим исходный и модулированный сигнал, а также спектр модулированного сигнала

2. Смоделируем два низкочастотных гармонических сигнала с частотами сигналов.

Смоделируем высокочастотный несущий сигнал , .

Получим модулированный сигнал для различных значений индекса угловой модуляции. Построим исходный и модулированный сигнал, а также спектр модулированного сигнала .

Смоделируем два моделирующих сигнала и квадратурный сигнал.

3. Смоделируем процесс демодуляции квадратурного сигнала и построим их спектры.

Пример программы, выполненной в среде Matlab, приведен в Приложении 4.