Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Нефтяной Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методичка для тех.спец. математика

.PDF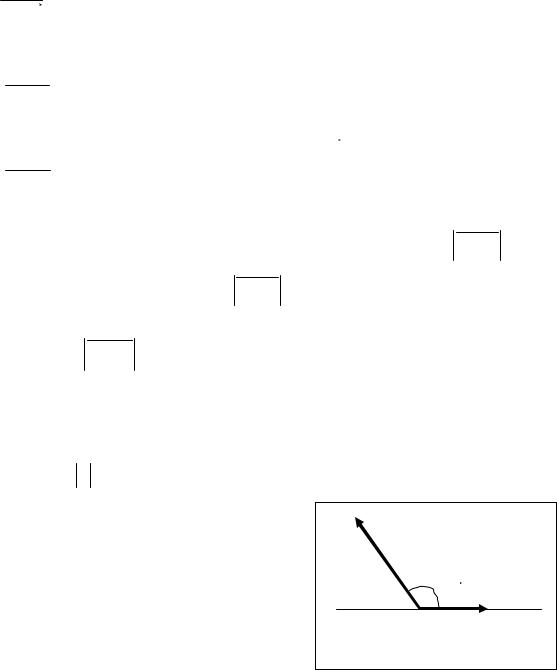

Скачиваний:

Добавлен:

17.03.2015

Размер:

2.25 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 163 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

				19
	прl a .							(1)
		→
	Так как A1B1 и l0			коллинеарны, то согласно теореме 1 из §3 и (1)
		r	→	r
	прl a		= A1B1 = λl0 ,					(2)
где λ − числовой коэффициент пропорциональности, называемый скалярной
проекцией вектора a на ось l и обозначаемый прl a . Таким образом,
		r	r
	прl a		= (прl a)l0 .					(3)
	Согласно (3) геометрический смысл скалярной проекции заключается в
				→
следующем:		это	есть величина вектора A1B1 , то		есть		длина A1B1 ,	если
→	r				→		r
A1B1 −− l0		и взятая со знаком минус A1B1 , если A1B1					−↓ l0 . Следователь-
но, скалярная проекция
		r		r
	прl a		= ± прl a .					(4)
	Теорема 1. Равные векторы имеют равные проекции.
	Теорема 2. Один и тот же вектор имеет равные проекции на сонаправ-
ленные оси.
	Теорема 3.		r
		r	r	ϕ ,
	прl a = a cos			ϕ ,				(5)
где ϕ (0 ≤ ϕ ≤ π) − величина угла, образованно-					A
го вектором a с осью l				(с вектором l0 ) (см.	A
го вектором a с осью l				(с вектором l0 ) (см.
рис.3).							ϕ
10 .	r		r
10 .	прl (a + b)= прl a + прl b − проекция сум-
мы векторов равняется сумме проекций слагае-					∙		l0	l
мы векторов равняется сумме проекций слагае-					∙		T
мых векторов.					A	1	T
мых векторов.						1
20 .	прl λa = λпрl a −			числовой множитель			Рис. 3
можно выносить за знак проекции.
	Замечание.		В дальнейшем нам будет встречаться термин: проекция a на
				r
направление вектора l (прl a) проекция на ось, для которой l − направ-
ляющий вектор и он же определяет положительное направление оси l.
	В дальнейшем, если не оговорено противное, векторный базис предлага-
ется ортонормированным.

§6. Скалярное произведение двух векторов и его свойства

1.ОПРЕДЕЛЕНИЕ 1. Скалярным произведением двух векторов a и b называется число (скалярная величина), обозначаемое одним из символов

(a, b), ab, (ab) и определяющееся по правилу

→ →

cos ϕ,

0 ≤ ϕ ≤ π .

(1)

a b

Другими словами, скалярное произведение равно произведению длин

векторов на косинус угла между ними.

→ →

Свойства: 10 . a b

прbr a =

прar b .

→ →

> 0 ϕ − острый угол: 0 ≤ ϕ <

π .

20 . a b

→ →

ϕ − тупой угол:

< ϕ ≤ π .

a b < 0

→ →

Рис. 1

30 . Если a , b ¹ 0, то

→ →

→

→ →

a b

= 0 a b .

(2)

либо хотя бы один из векторов - нулевой.

. a b

0 Û j =

;

Теорема 1.

Если a{a1 , a 2 , a 3 }, b{b1 , b2 , b3 }, то скалярное произведе-

ние равно сумме произведений одноименных координат множителей

→ →

= a1b1 + a 2b 2 + a 3b 3 .

a b

(3)

ОПРЕДЕЛЕНИЕ 2.

Скалярным квадратом вектора a

(a 2 ) называется

скалярное произведение вектора a на себя.

Из (1) следует

a 2

, т.е. скалярный квадрат вектора равняется квад-

рату его длины. Отсюда, согласно (1) и (3),

a12 + a22 + a32 .

(4)

→ →

a , b

b, a − коммутативность скалярного произведения.

→ →

− числовой множитель можно выно-

λ a , b

= a , λ b

= λ a , b

сить за знак скалярного произведения.

→

→ →

Следствие.

λ a , μ b

= λμ a , b .

→ → →

→ →

a + b, c

= a , c

+ b, c

− распределительное свойство по отно-

шению к первому множителю;

→ → →

→ →

− распределительное свойство по отноше-

a , b

+ c =

a , b

+ a , c

нию ко второму множителю.

2. Приложения скалярного произведения, в пер-

вую очередь, определяются формулами (см. рис.2):

cos ϕ =

(5)

где ϕ − угол между векторами a

и b .

Рис. 2

r r

прbr a

= (a, b0 ).

(6)

Работа силы F по перемещению единичной массы из т. A в т. B по пря-

молинейному отрезку AB равна F

Направляющие косинусы вектора (см.

рис. 3): cos α, cos β, cos γ , где

(7)

α = a

ˆ i; β = a ˆ j; γ = a ˆ k;

a{a1 , a 2 , a 3 }: a = a1 i + a 2 j + a 3 k

i{1,0,0}, j{0,1,0}, k{0,0,1}.

Рис. 3

При этом

a1a2a3

= пр

cos α

= ai

= прr a

i r

x r

cosβ

= aj

= прr a

= прy a

(8)

r r

j r

cos γ

= ak = прkr a = прz a =

Последние три равенства определяют геометрический смысл координат вектора в ортонормированном базисе: проекции вектора на оси координат, положительное направление которых определяются базисными векторами. Отсюда

cos α =

Орт вектора

		r
r	=	a
a0		r
a0		r
		a

β =

; cos γ =

; cos

(9)

a вектор

= {cos α, cos β, cos γ}.

(10)

Другими словами, направляющие косинусы вектора - это координаты

								22
орта этого вектора. В силу этого и (3)
		r						γ = 1.
		a02 = cos2 α + cos2 β + cos2						γ = 1.		(11)
ПРИМЕР 1. Найти вектор x , образующий со всеми тремя базисными ор-
			r	= 2
тами равные острые углы, если			r					3 .
тами равные острые углы, если			x					3 .
1.Решение. Согласно условию и (10)										имеем α = β = γ, cos2 a =	1	,
1.Решение. Согласно условию и (10)										имеем α = β = γ, cos2 a =		,
	1						1			3
cos a =		. Согласно (8) x1 = 2				×			= 2 = x	2 = x 3 .
					3

3
3								3

r{ }

Ответ: x 2;2;2 .

§7. Векторное произведение двух векторов и его свойства

1.ОПРЕДЕЛЕНИЕ 1. Упорядоченная тройка некомпланарных векторов

→→ →

a , b, c , приведенная к общему началу, называется правой при условии, что если смотреть с конца третьего вектора c , то кратчайший поворот от первого

вектора

ко

второму

вектору b должен про-

исходить

против часо-

вой стрелки (см. рис. 1).

Правая

Левая

тройка

противном

случае

тройка

T ϕ

упорядоченная

тройка

→ → →

a , b, c называется ле-

вой (см. рис. 2).

Рис. 1

Рис. 2

(Упомянутый кратчайший поворот от первого вектора ко второму должен

происходить против часовой стрелки на угол 0 ≤ ϕ ≤ π).

Замечание. Если три вектора упорядочены (занумерованы), то запись

a, b, c , означает: a - первый вектор,

b - второй вектор,

c - третий вектор. Ес-

ли же мы пишем c, a, b ,

то c - первый вектор, a - второй вектор,

b - третий

вектор.

ОПРЕДЕЛЕНИЕ 2. Векторным произведением упорядоченной пары

→ →

векторов

a , b

называется третий вектор, обозначаемый одним из символов

´ b и определяющийся из трех нижеследующих условий:

[ab],[a, b],a

r r

sin j ; 2

0 .

[a, b]

[a, b]^

образует правую тройку, если [a, b]

¹ 0.

r	30	r	r
a, b ;		. Тройка векторов a, b,[a, b]

			23
		r	r
Замечание. 10 [a, b]= 0			b = λa .
Для ненулевых неколлинеарных векторов
		r			D	C	B
и только в этом случае [a, b] ≠ 0 . Геометриче-					D	C	B
ский смысл 10			r r		[a, b]	b
ский смысл 10	состоит в том, что [a, b] равен					b
площади параллелограмма TABC (см. рис. 3),						ϕ
площади параллелограмма TABC (см. рис. 3),							A
построенного на векторах a и b как на сторо-					T	a	A
построенного на векторах a и b как на сторо-					T	a
нах после приведения их к общему началу T .						Рис. 3
Условие	20	означает,	что векторное			Рис. 3
Условие	20	означает,	что векторное
произведение перпендикулярно к векторам a				и	b . Требование 30		говорит о
том, что если смотреть с конца вектора [a, b],				то кратчайший поворот на угол

ϕ(0 < ϕ < π) от a к b должен происходить против часовой стрелки.

2.Свойства:

	r	r
10 ) [a, b]= −[b, a], т.е. векторное произведение антикоммутативно.
20 )	r	r	r	r
20 )	[λa, b]= λ[a, b];		[a,µb]= µ[a, b], т.е. числовой множитель можно вы-
носить (вносить) за (под) знак векторного произведения.
Следствие.		r		r
Следствие.		[λa,µb]= λµ[a, b].
				r	r	r r	r
30 Распределительное свойство: [a					+ b, c]= [a, c]+ [b, c];
r	r	r	r r
[a, b + c]=		[a, b]+ [a, c].

r	, a 2	, a 3 }, b{b1 , b2 , b3 } в правом ортонормированном базисе, то
Если a{a1

координаты [a, b] определяются с помощью символического определителя

третьего порядка:

r r

a 2

a 3

[a, b]=

= i

− j

+ k

;

b 2

b 3

b 2

b 3

b 2

r r

−

(1)

[a, b]

b 2

b 3

b 2

Задача 1.

Найти координаты вектора x , если он перпендикулярен к век-

торам

a1{2,−3,1}

a 2 {1,−2,3},

также

удовлетворяет условию

x(i + 2 j − 7k)= 10 .

Решение.

Из условия задачи имеем x = λ[a1

, a 2

], x i +

2 j − 7k

= λ[a1

, a 2 ](i + 2 j − 7k)= 10 ;

10[a

1 , a 2 ]

λ =

r r

; x =

r r

[a1 , a 2

](i

2 j − 7k)

[a1

, a 2

](i

2 j − 7k)

Теперь остается воспользоваться формулой (1) и дове-

сти задачу до конца, а именно

a 2

r r

] =

− 3 1

2 1

2 − 3

[a1 ; a 2 ]

− 3 1

− j

[a1

, a 2

= i

− 2

+ k

−

− 2

Рис. 4

= −7 i − 5 j − k

](i + 2 j − 7k)= −7 −10

+ 7 = −10 .

[a1

, a 2

В силу этого x = −[a1 , a 2 ] {7,5,1}.

r{ }

Ответ: x 7,5,1 .

§8. Смешанное произведение трех векторов и его свойства

1.Рассмотрим упорядоченную тройку векторов

r r
r r
a, b, c .				[a, b]
ОПРЕДЕЛЕНИЕ.		Смешанным произведени-		[a, b]
r	r	называется число (скаляр-
ем тройки векторов a, b, c		называется число (скаляр-	с	b
	r	r	с	b
ная величина), равное ([a, b], c).				T
Геометрический смысл знака смешанного про-				T
Геометрический смысл знака смешанного про-				a
изведения: если ϑ − объем параллелепипеда, постро-				Рис. 1
r	r			Рис. 1
енного на векторах a, b, c как на сторонах, то
енного на векторах a, b, c как на сторонах, то
r r	r	r
[a, b]c = ϑ, если	a, b, c образуют правую тройку;

−ϑ, если a, b, c образуют левую тройку.

Теорема.			r	r
			[a, b] c = 0 когда векторы компла-					•c
нарны, т.е.		после приведения к общему началу лежат в
одной плоскости.							•
2.	При циклической перестановке векторов сме-
								•
шанное			произведение		не	меняется:	a		b

r r	r	r	r r	]b . В силу этого принято обозначе-
[a, b]c = a[b, c]= [c, a								Рис. 2
r	r	r	r

ние [a, b]c = abc, показывающее,					что результат не за-

висит от того, как расставить квадратные скобки в правой части.

В координатах множимых векторов смешанное произведение определяется так:

r rr

abc

(1)

, b

2 , b

где a{a1 , a 2 , a 3 }, b(b1

3 ), c(c1 , c2 , c3 ).

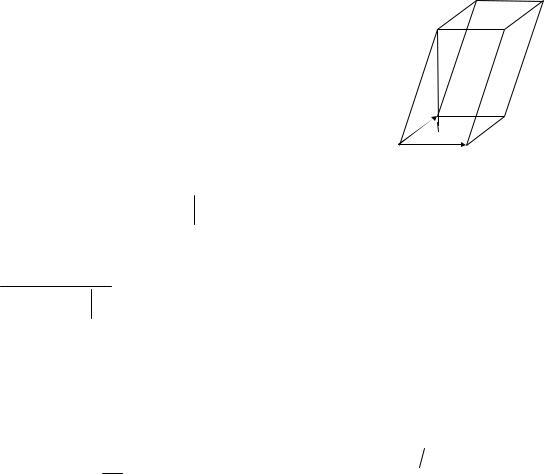
ПРИМЕР 1. Найти длину высоты

D′

C′

параллелепипеда ABCDA′B′C′D′, опу-

щенной из вершины

A′

на

основание

A′

B′

ABCD . A(1,2,−3), B(2,4,0),

D(2,3,0),

A′(5,3,1).

ϑ =

Решение.

AA′

= S h, h = A′E, E −

основание

перпенди-

куляра, опущенного из т. A′ на плоскость

ABCD .

[

]

Рис. 3

SABCD = S =

. Тогда

AB,

h =

AB,

AD,

AA′

{1,2,3},

{1,1,3},

[

]

AA′{4,1,4}.

[AB, AD]=

= i

− j

+ k

= 3i

− k ;

[

]{3,0,−1};

h =

AB,

AA′ = 12 − 4 = 8;

Ответ: 810 .

ГЛАВА III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ

Учебники: Ефимов Н.В., гл. 1-7, § 11-13. Беклемишев Д.В., гл. II, III.

§1. Прямая на плоскости

1.Различные виды уравнений прямой. Геометрический смысл коэффици-

ентов.

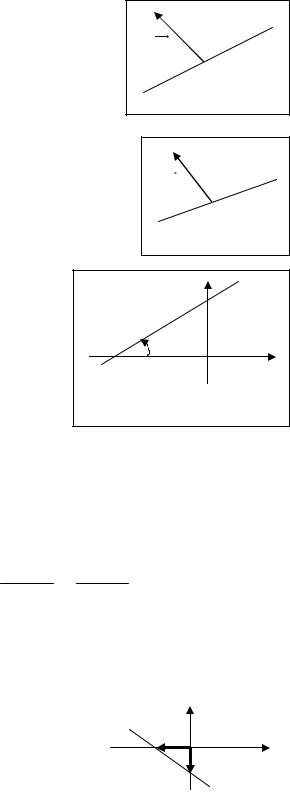
1) a : Ax + By + C = 0 − общее уравнение прямой.

N{A, B}− нормальный вектор прямой, т.е. направляющий вектор прямой, перпендикулярный к заданной прямой;

				26
a{− B, A}− направляющий вектор прямой, т.е. вектор, параллельный пря-
мой либо лежащий на этой прямой;
C = 0 когда прямая проходит через начало ко-								a
ординат;							N	a
ординат;							N
C ≠ 0 когда прямая не проходит через начало
координат (см. рис. 3), x, y − координаты произвольной							Рис. 1
(текущей) точки прямой.
2)	A(x − x0 ) + B(y − y0 ) = 0 − уравнение прямой,
проходящей через т. M 0 (x0 , y0 ) , перпендикулярно векто-							N	M 0
ру N{A, B}, т.е.		N − нормальный вектор прямой (см.					N	M 0
ру N{A, B}, т.е.		N − нормальный вектор прямой (см.						•
рис. 2).							Рис. 2
Уравнение		прямой	с	угловым	коэффициентом:		Рис. 2
Уравнение		прямой	с	угловым	коэффициентом:
y = kx + b, k = tgα, α − угол				наклона	прямой с		y
осью x .							y
осью x .	→							Q
	→							Q
b = вел. OQ, Q(0, b) − точка пересечения прямой						P	α
с осью y (см. рис. 3).						P	α
с осью y (см. рис. 3).						a	0	x
3)	Параметрические			уравнения	прямой:	a	0	x
3)	Параметрические			уравнения	прямой:
x = x 0	+ mt						Рис. 3
	.
y = y0	+ nt							(x0 , y0 ) −
(x, y) − координаты текущей (произвольной) точки прямой;								(x0 , y0 ) −
координаты начальной точки прямой. Начальной точкой считается фиксиро-
ванная точка прямой; a{m, n} − направляющий вектор прямой, t − параметр,

tR .

4)Каноническое уравнение прямой: x − x 0 = y − y0 . Уравнение прямой,

проходящей через две точки M1 (x1 , y1 ),

M 2 (x 2

, y 2 ) :

x − x1

y − y1

x 2 − x1

y 2 − y1

5) Уравнение прямой в отрезках

= 1.

a b

P(a,0), Q(0, b) − точки пересечения прямой с осями

координат (см. рис. 4), при этом

a = вел.

, b = вел.

. В этом состоит

геометрический смысл параметров a и b уравнения

Рис. 4

прямой в отрезках.

2. Расстояние от точки до прямой определяется по формуле

P(M* , a)=

Ax* + By* + C

= A

+ B2 ,

(1)

где M* (x* , y* ), прямая задана общим уравнением

(см. рис. 5).

Следовательно, надо взять левую часть Ax + By + C общего уравнения прямой и вместо x и y подставить со-

ответственно x* и y* − координаты т. M * . Далее, остается модуль полученной суммы поделить на модуль N .

	• M*
M 0	•
	Рис. 5

3. Взаимное расположение 2-х прямых на плоскости a1 : A1x + B1y + C1 = 0; a2 : A 2 x + B 2 y + C2 = 0 .

I) a1 I a 2 N 2 ≠ N1


	A 2	≠			B2	.
	A1				B1

II) a1 \|\| a 2			N2 = λN1
	A 2		=	B2		≠	C1	.
	A1
					B1		C2

III) a1 ≡ a 2 : условие совпадения двух прямых:

(2)

(3)

(4)

A 2

(5)

4. ОПРЕДЕЛЕНИЕ. Углом между

двумя прямыми (см. рис.6) называется из

2-х смежных углов, образованных

этими

прямыми.

a1{− B1

, A1}

Формула

(N1

, N 2 )

)

, a

a 2 {− B2 , A 2 }

cos ϕ =

(6)

N 2

Рис. 6

определяет острый угол между двумя пря-

мыми a1

a 2 .

Обычно выбирают острый

угол.
(6) a1 a 2 N1 N 2
A1 A 2 + B1B2 = 0 .	(7)

Задача 1. Составить уравнения сторон и диагонали ромба, если известны уравнения двух его сторон x + 2y = 4 и x + 2y = 0 и уравнение одной из диагоналей y = x + 2 .

Решение.

a1 : x + 2y = 4; c : y = x + 2

: x + 2y = 0 .

Согласно (4) a1 || a 2 ,

схематический чер-

a 2

теж дан на рис. 7. Согласно этому чертежу

y = x + 2

P = c I a2

Рис. 7

x + 2y = 0

x = − 4 3

y = x + 2

x = 0

Q(0,2) Середина отрезка PQ

P(− 4 3, 2 3); Q = c I a1 :

x + 2y = 4

y = 2

под прямым уг-

точка T −

;

. Теперь вспомним, что диагонали ромба I

лом:

(SR ) с. Направляющий вектор c {1;1} прямой c − нормальный вектор

прямой (SR ). В силу этого имеем

							2													4
(SR ):1 x +									+1 y −												= 0; 3x + 3y − 2										= 0.
(SR ):1 x +									+1 y −												= 0; 3x + 3y − 2										= 0.
							3													3
																															= 4 −			20			= −			8
x + 2y = 4																x = 4 − 2y													x															8 10
x + 2y = 4																x = 4 − 2y													x															8 10
S :							= 2													− 6y + 3y = 2												10		3						3, S			−		,
S :																																		3						3, S			−		,
3x + 3y																12														y =														3 3
																														y =			3
																																	3
x + 2y = 0																x = −2y									x = 4 3									4				2				4				8
x + 2y = 0																x = −2y									x = 4 3									4				2				4				8
R :																			= − 2 3												, R				;−				, SP					;−			.
R :																															, R				;−				, SP					;−			.
3x + 3y							= 2									y									y		= − 2 3							3 3								3				3
8														10
(SP):	x +					=				y		−					,		3x + 8				=		3y −10				: 3x + 8 = −							3y −10					;
	x +			3						y		−			3				3x + 8						3y −10											3y −10
														8					4
			4								−			8					4						− 8													2
3											−			3
3														3
6x + 3y + 6 = 0; 2x + y + 2 = 0 .
4															2
(QR ):		x −						=			y +							; 2x −				8		+ y +		2		= 0; 2x + y − 2 = 0 .
		x −			3						y +					3						8				2

			−1										2						3						3

Ответ: (SR ): 3x + 3y − 2 = 0; (SP): 2x + y + 2 = 0; (QR ): 2x + y − 2 = 0 .

§2. Плоскость

1.Различные виды уравнений плоскости. Геометрический смысл коэф-

фициентов.

1) α : Ax + By + Cz + D = 0 − общее уравнение плоскости.

<<< < Предыдущая 1 23 / 163 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.12.2018573.95 Кб56Методичка ГРЭС.doc
#
17.03.2015438.27 Кб41методичка для ГЛ, ГФ.doc
#
26.08.2019463.87 Кб10методичка для дипломников по экономике.doc
#
04.12.2018238.59 Кб8Методичка для заочников (У.Г.Г.).doc
#
17.03.2015696.83 Кб45методичка для ЗО по английскому.doc
#
17.03.20152.25 Mб8Методичка для тех.спец. математика.PDF
#
17.03.2015386.56 Кб130Методичка для ФТТ(ТЭ).doc
#
09.11.2019555.01 Кб3методичка для ФТТ.doc
#
17.03.20151.23 Mб186Методичка ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ.doc
#
20.11.20185.4 Mб12методичка интернет-тестирование.doc
#
11.11.2018379.39 Кб3Методичка к курсовой по ТОЭ1.doc