Силы и моменты, действующие на ракету в полете. Аэродинамические силы

 

Силовое воздействие сплошной газообразной среды сводится к непрерывно распределенным по поверхности тела силам от нормальных напряжений и от касательных напряжений. Все аэродинамические силы, действующие на ракету в полете можно свести к одной результирующей силе R_A (главная аэродинамическая сила), а также к результирующему моменту М_А, действующему относительно центра масс ракеты.

R_A проходит через точку на продольной оси ракеты, которая носит название центр давления.

Величина и направление R_A и М_А зависят от ряда факторов, в том числе: от угла атаки, плотности воздуха, скорости воздушного потока, аэродинамической формы ракеты и т.д. Известно, что R_A в наибольшей степени, кроме формы ракеты, зависит от угла атаки и от угла скольжения.

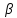Для того, чтобы было удобно составлять уравнения движения, принято R_A и М_А раскладывать по осям систем координат (рис. 10).

– По осям скоростной системы координат R_A есть: .

Проекция R_A на ось OX_n () всегда отрицательна и носит название силы лобового сопротивления;

– подъемная сила;

– боковая сила.

– По осям связанной системы координат R_A есть: .

Здесь Х₁ – продольная (осевая) сила; Y₁ – нормальная сила; Z₁ – поперечная сила.

Баллистическая ракета является аэродинамически осесимметричным телом. Если продольная ось ракеты направлена по вектору скорости (т.е. 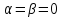), то обтекание ракеты воздушным потоком будет симметричным относительно плоскости, проходящую через эту ось, т.е.Y₁ = Y = 0; Z₁ = Z = 0.

Если ось ракеты образует с вектором скорости некоторый угол, то обтекание ракеты воздушным потоком будет симметричным относительно плоскости, проходящей через ось ракеты и вектор скорости. При этом R_A и ее составляющие (X,X₁,Y,Y₁) будут лежать в этой плоскости, следовательно, для аэродинамики симметричной ракеты зависимости силы Z(Z₁) от угла скольжения аналогичны зависимостям силыY(Y₁) от угла атаки .

На основании теории аэродинамического подобия проекции аэродинамической силы на оси системы координат (связанной или скоростной) равны:

,

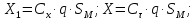
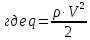– скоростной напор, действующий на ракету;

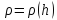– плотность воздуха на высоте полета;

V – скорость ракеты;

S_м – характерная площадь ЛА (для бескрылого ЛА или фюзеляжа это площадь наибольшего – миделевого сечения), которая для ракеты равна;

, где D_м – диаметр цилиндрической части ракеты;

– безразмерные аэродинамические коэффициенты.

Аэродинамические коэффициенты зависят от формы ракеты, ее ориентации относительно вектора воздушной скорости (т.е. от величины углов ), а также от критериев аэродинамического подобия.

Критериями аэродинамического подобия являются:

– число Маха ;

– число Рейнольдса ;

здесь а = а(h) – скорость звука в воздушной среде на данной высоте; l – характерный размер ЛА (для ракеты – длина ракеты); – динамический коэффициент вязкости воздуха.

Отличие реальной скорости ракеты от характеристической

Поскольку в условиях реального полёта на ракету кроме тяги двигателей действуют и другие силы, то скорость, развиваемая ракетами в этих условиях, как правило, ниже характеристической из-за потерь, вызываемых силами гравитации, сопротивления среды и др. Действительная скорость в конце активного участка траектории должна рассчитываться с учетом этих потерь:

Формулу для расчета скорости с учетом потерь называют иногда формулой Королева.

В таблице 1 приведён баланс скоростей ракеты Сатурн Vпри выводе корабляАполлонна траекторию полёта к Луне.

Таблица 1.