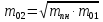Приращение скорости ракеты

№ п/п	Ступень ракеты	Приращение скорости, %
		двухступенчатая	трехступенчатая
1	Первая	40	27
2	Вторая	60	35
3	Третья	–	38

Таблица 3

Соотношение масс ступеней ракеты

Число ступеней	Ракеты с ЖРД	Ракеты с РДТТ
2
3

Элементы небесной механики

Небесная механика– раздел астрономии, применяющий законы механики для изучения движения небесных тел. Небесная механика занимается предвычислением положения Луны и планет, предсказанием места и времени затмений, в общем, определением реального движения космических тел.

Естественно, что небесная механика в первую очередь изучает поведение тел Солнечной системы (обращение планет вокруг Солнца, спутников вокруг планет, движение комет и других малых небесных тел). Тогда как перемещение далеких звёзд удается заметить, в лучшем случае, за десятилетия и века, движение членов Солнечной системы происходит буквально на глазах – за дни, часы и даже минуты. Поэтому его изучение стало началом современной небесной механики, рождённой трудами И. Кеплера (1571—1630) и И. Ньютона (1643—1727). Кеплер впервые установил законы планетного движения.

Законы Кеплера

Законы Кеплера – это три эмпирических соотношения, интуитивно подобранных Иоганном Кеплером на основе анализа астрономических наблюдений Тихо Браге. В рамках классической механики выводятся из решения задачи двух тел предельным переходом , где,– массы планеты и Солнца соответственно.

Первый закон Кеплера (закон эллипсов)

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце (рис. 36).

Форма эллипса и степень его сходства с окружностью характеризуется отношением , где– расстояние от центра эллипса до его фокуса (половина межфокусного расстояния),a – большая полуось. Величина называется эксцентриситетом эллипса. При, и, следовательно,эллипс превращается в окружность.

Рис.36

Второй закон Кеплера (закон площадей).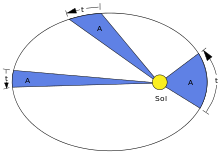

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади (рис.37).

Применительно к нашей Солнечной системе, с этим законом связаны два понятия: перигелий – ближайшая к Солнцу точка орбиты, и афелий – наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.

Рис.37

Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

Третий закон Кеплера (гармонический закон)

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет (это соотношение справедливо не только для планет, но и для их спутников):

Где и– периоды обращения двух планет вокруг Солнца, аи– длины больших полуосей их орбит.

Ньютон вывел из законов Кеплера закон всемирного тяготения и использовал законы движения и тяготения для решения небесно-механических проблем, не охваченных законами Кеплера. После Ньютона прогресс в небесной механике в основном заключался в развитии математической техники для решения уравнений, выражающих законы Ньютона. Таким образом, принципы небесной механики – это «классика» в том смысле, что и сегодня они такие же, как во времена Ньютона. Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен – в действительности в него входит и масса планеты: , где– масса Солнца, аи– массы планет.

Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.

Применение результатов небесной механики к движению искусственных спутников и космических кораблей составляет астродинамику

Астродинамика – раздел небесной механики, изучающий движение искусственных космических тел: искусственных спутников, межпланетных станций и других космических кораблей. В сферу задач астродинамики входят расчёт орбит космических кораблей, определение параметров их запуска, вычисление изменений орбит в результате манёвров, планирование гравитационных манёвров и другие практические задачи. Результаты астродинамики используются при планировании и проведении любых космических миссий. Астродинамика выделяется из небесной механики, которая изучает в первую очередь движение естественных космических тел под действием сил тяготения, своей ориентированностью на решение прикладных задач управления космическими кораблями. В связи с этим в астродинамике требуется учитывать и факторы, игнорируемые классической небесной механикой – влияние атмосферы и магнитного поля Земли, гравитационных аномалий, давления солнечного излучения и другие.

Орбита (отлат.Orbita— колея, дорога, путь) – траектория движения материальной точки в наперёд заданной системе пространственных координат для заданной в этих координатах конфигурации поля сил, которые на неё действуют.

В небесной механике это траектория небесного тела в гравитационном поле другого тела, обладающего значительно большей массой (планеты, кометы, астероида в поле звезды). В прямоугольной системе координат, начало которой совпадает с центром масс, траектория может иметь форму конического сечения (окружности, эллипса, параболы или гиперболы). При этом его фокус совпадает с центром масс системы.

Долгое время считалось, что планеты должны иметь круговую орбиту. После долгих и безуспешных попыток подобрать круговую орбиту для Марса, Кеплер отверг данное утверждение и, впоследствии, используя данные измерений, сделанных Тихо Браге, сформулировал три закона, описывающих орбитальное движение тел.

Кеплеровыми элементами орбиты являются (рис. 38):

• фокальный параметр⁵, большая полуось,радиус перицентра ирадиус апоцентра⁶— определяют размер орбиты,

• эксцентриситет(e)— определяет форму орбиты,

• наклонение орбиты (i),

• долгота восходящего узла (Ω) – определяет положение плоскости орбиты небесного тела в пространстве,

• аргумент перицентра(ω) – задаёт ориентацию аппарата в плоскости орбиты (часто задают направление на перицентр),

  Рис.38

• момент прохождения небесного тела черезперицентр() – задаёт привязку по времени.

Эти элементы однозначно определяют орбиту независимо от её формы (эллиптической, параболической или гиперболической). Основной координатной плоскостью может быть плоскость эклиптики, плоскость галактики, плоскость земного экватора и т. д. Тогда элементы орбиты задаются относительно выбранной плоскости.

По геометрической формеорбиты делятся на круговые и эллиптические, с тем или иным эксцентриситетом. Также существует разделение на замкнутые и незамкнутые орбиты, в особенности для КЛА.

По углу наклоненияiплоскости орбитык плоскости земного экватора – на экваториальные (i = 0°), полярные (i = 90°) и наклонные (i– любое, кроме 0° и 90°).

По соотношению периода обращенияТ_обвокруг земного шара с земными или солнечными сутками – на не синхронные, квазисинхронные, синхронно-суточные (геосинхронные), солнечно-синхронные.

Орбитальная скорость тела (планеты,естественногоилиискусственного спутника, звезды) – это скорость, с которой оно вращается вокругбарицентрасистемы, как правило, вокруг более массивного тела (табл. 4).

Таблица 4