2.Явление внутреннего трения. Коэффициент внутреннего трения.

Явление внутреннего трения относится к процессам, объединенным общим названием явлений переноса, суть которых состоит в следующем: если в веществе существует пространственная неоднородность плотности, температуры или скорости упорядоченного перемещения отдельных слоев вещества, то хаотическое движение молекул выравнивает эти неоднородности.

Внутреннее трение в жидкостях и газах по своей природе отличается от "внешнего трения" - трения между твердыми телами. Явления внутреннего трения (вязкости) связано с возникновением сил трения между слоями жидкости или газа, перемещающимися параллельно друг другу с различными по величине скоростями.

Механизм возникновения силы внутреннего трения можно пояснить следующим примером.

Рис.5 Рис. 6

Рассмотрим ламинарное движение газа при котором движущейся газ как бы разделяется на слои, которые при своем направленном движении не перемешиваются, как бы скользят относительно друг друга.

Пусть слой А газа (рис.5) перемещается направлено со скоростью, слой В, перемещается параллельно слою А направлено со скоростью. В силу хаотического теплового движения молекулы слоя А будут переходить в слой В и приносить в этот слой импульсы , где m₀ масса одной молекулы; молекулы слоя В будут переходить в слой А и приносить импульсы. Если, то молекулы слоя А начнут тормозиться, а молекулы слоя В - ускоряться, т.е. изменится скорость направленного перемещения слоев, что приведет к появлению ускорения, которое по второму закону Ньютона, должно быть вызвано действием какой-либо силы. Силу, вызывающую изменение скорости направленного движения параллельно движущихся слоев жидкости или газа, и называют силой внутреннего трения.

Для вывода количественных соотношений, характеризующих внутреннее трение, рассмотрим случай, когда движение слоев в покоящемся газе вызвано движением вверх (или вниз) перпендикулярно оси Х плоской пластины, обладающей скоростью, (рис.6). В своем движении пластина увлечет прилегающий к ней слой газа, который в свою очередь увлекает за собой следующий слой и т.д. Таким образом весь газ как бы делится на тончайшие слои, скользящие вверх тем медленнее, чем дальше они находятся от движущейся пластины.

Пусть вектор представляет собой скорость направленного движения произвольного слоя в газе. Тогда каждая молекула газа этого слоя участвует в двух движениях: хаотическом (тепловом) со средней скоростью и направленном (коллективном) со скоростью. Из молекулярной физики известно, что средняя скорость хаотического движения по абсолютной величине очень велика, так что  . Однако направление вектора скорости из-за столкновения с молекулами непрерывно и хаотически изменяется так, что вектор средней скорости в среднем равен нулю: =0, т. е. совокупность непрерывно сталкивающихся молекул, участвующих только в тепловом движении в среднем будет оставаться на месте. При наличии же дополнительного направленного движения вся совокупность молекул в целом будет дрейфовать с постоянной скоростью , таким образом, средний импульс отдельной молекулы в данном слое равен:

, (8)

т.е. на импульс молекулы тепловое движение не оказывает влияние.

Для расчета силы внутреннего трения рассмотрим контрольную площадку S, расположенную перпендикулярно оси на произвольном расстоянии х от движущейся пластины (рис.6).

Ввиду хаотичности теплового движения молекул можно считать , что вдоль оси Х движется одна треть от общего числа молекул (другая 1/3 молекул - вдоль оси Y , остальная 1/3 - вдоль оси Z), причем половина из каждой 1/3 молекул движется слева направо, а другая половина - справа налево. Тогда через площадку S за время t слева направо (т.е. в положительном направлении оси Х) пролетит число молекул N₊, занимающих объем V=St параллелепипеда площадью основания S и длиной стороны, равной t :

N₊ = 1/6  n V = 1/6  n S t.

Аналогично, справа налево, т.е. в отрицательном направлении оси Х, через площадку S пройдет число молекул N-

N- = 1/6  n S t.

Импульс, перенесенный каждой движущейся молекулой равен произведению массы m₀ одной молекулы на скорость переносного движения. Однако, т. к. скорость при переходе от слоя к слою на протяжении t изменяется, то будем считать, что площадку S молекулы пересекают, обладая тем значением скорости переносного движения, которую они приобрели в результате последнего столкновения на расстоянии средней длины свободного пробега от S (слева это будет координата Х₁ = Х - , справа - Х₂ = Х + ) Если скорость направленного движения слоя газа или жидкости в точке с координатой Х₁ обозначим через , а в точке с координатой Х₂ через , то импульс, перенесенный всеми молекулами слева направо через площадку S за время t будет равен

K₁ = m₀ N₊ = m₀ 1/6  n S t. (9)

Аналогично, импульс, перенесенный молекулами справа налево через площадку S за время t равен

K₂ = m₀ N_- = m₀ 1/6  n S t. (10)

Таким образом, тепловое хаотическое движение молекул приводит к тому, что на поверхности S соприкосновения слоев возникает изменение импульса, равное

K = K₁-K₂= m₀ N₊ - m₀ N_- = 1/6 m₀ n S t ( - ).

(11)

Основываясь на связи между силой и изменением импульса (F= (m )/ t=K/t), можно утверждать, что движение слоев происходит таким образом, как если бы вдоль поверхности между левым и правым прилегающими к ней слоями действовала сила трения, равная

F_тр= K/t=1/6 n m₀ S ( - ). (12)

По рисунку 6 за положительное направление оси X взято направление слева направо, поэтому как принято в математике приращение скорости в формуле (12) можно записать ( - )= - ( - ). Это изменение скорости происходит не скачкообразно, а постепенно и на расстоянии X₂- X₁= X =( X+)- (X-)=2. Поэтому изменение скорости по толщине площадки S происходит на величину d /dX, а на расстоянии 2 , соответственно (d /dX) 2 = - ( - ). Подставляя это в формулу (12) получим:

F_ТР=-1/6 m₀ c n S (d /dX)2 (12а)

или

F_ТР=-1/3 m₀ c n S (d /dX)  (13)

Введем обозначения в формуле (13):

= 1/3 m₀ n = 1/3  , (14)

где  = m₀ n - плотность газа или жидкости. Коэффициент пропорциональности  носит название коэффициента вязкости газа или жидкости. С учетом этого обозначения (13) перепишем в виде:

F_тр = -  S  /X, (15)

a коэффициент вязкости равен:

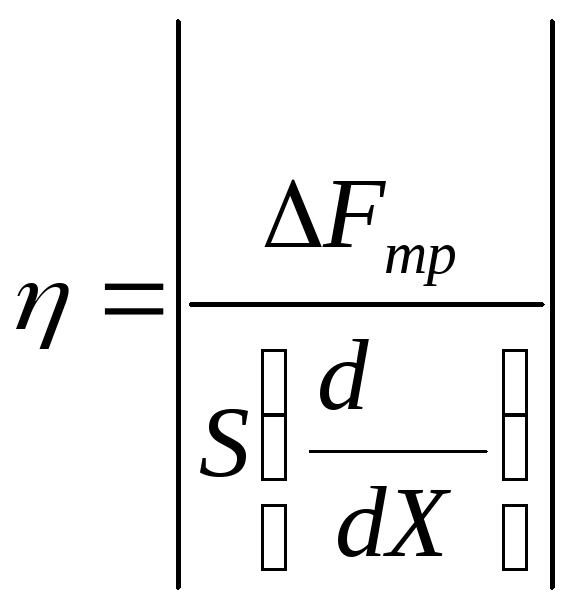, (16)

где величина  /X показывает изменение скорости направленного движения слоев с изменением расстояния вдоль оси, расположенной перпендикулярно этой скорости, т.е. представляет градиент скорости движения.

Сила внутреннего трения будет тормозить движение перемещающейся вверх пластины и поэтому направлена вниз (рис.6).

Из (15) и (16) видно, что сила внутреннего трения зависит прямопропорционально от коэффициента вязкости, градиента скорости и величины площади соприкасающихся слоев, а коэффициент вязкости числено равен силе внутреннего трения, действующей на единицу площади границы раздела параллельно движущихся слоев газа, когда скорость их движения изменяется на единицу при перемещении в направлении, перпендикулярном к границе, на единицу длины, т.е. при  /X =1.

Знак “минус” в формуле (15) обозначает, что импульс всегда переносится в направлении уменьшения скорости.

Единицей вязкости в СИ служит такая вязкость, при которой градиент скорости с модулем, равным 1м/с на 1м, приводит к возникновению силы

внутреннего трения в 1Н на 1м² поверхности касания слоев. Эта единица называется Паскаль-секундой (Па×с). Эти рассуждения можно отнести и к жидкостям.

Следовательно, вязкость зависит от рода жидкости или газа и их температуры, причем для жидкостей вязкость сильно уменьшается с повышением температуры. У газов, наоборот, вязкость растет с увеличением температуры. Такую зависимость для газов можно объяснить следующим образом: из формулы (14) видно, что h зависит от n, m₀, с и l. Из молекулярно-кинетической теории газов известно, что средняя арифметическая скорость

,

а из формулы (5) обратно пропорциональна n·d²_эф. Подставив все эти величины в формулу (14), мы получим, что коэффициент вязкости зависит прямо пропорционально от :

;

т. е, h для газов не зависит от концентрации n и давления p равного

p = nkТ.

Однако это утверждение остается справедливым только для среднего атмосферного давления. При давлениях, превосходящих в 10 раз и более атмосферное, а также для очень разряженного газа внутреннее трение начинает снова зависеть от давления.