
- •1. Основные понятия и определения теории дифференциальных уравнений
- •2. Дифференциальные уравнения первого порядка с разделяющимися переменными
- • Заменив y' на , а затем, умножив все члены наdx, получим
- •3. Однородные дифференциальные уравнения первого порядка
- •Определение 1.Функция f(X,y) называется однородной функцией n-ого измерения (n-ой степени) относительно переменных X и y,если при любом t справедливо тождество
- •Пример 1.Решить уравнение .
- •4. Линейные дифференциальные уравнения первого порядка Линейное дифференциальное уравнение первого порядка имеет вид
- •5. Уравнения в полных дифференциалах
- •6. Уравнения второго порядка, допускающие понижение порядка
- •Уравнение вида
- •Теорема о структуре общего решения
Уравнение вида
|
|
(6.9) |
не содержит явным образом искомой
функции
![]() .
.
Полагая
![]() и
и![]() ,
получим уравнение первого порядка
,
получим уравнение первого порядка![]()
с неизвестной функцией
![]() .
Проинтегрировав это уравнение, находим
его общее решение:
.
Проинтегрировав это уравнение, находим
его общее решение:![]() а затем из соотношения
а затем из соотношения![]() получаем общий интеграл уравнения
(6.9):
получаем общий интеграл уравнения
(6.9):
![]() .
.
Пример 4. Решить уравнениеx(y''+1) +y' =0 (x0).
Полагая
![]() откуда
откуда![]() получим
получим
![]()
или
![]() .
Это
уравнение – однородное. Полагаем
.
Это
уравнение – однородное. Полагаем![]() .
.
Цепочка преобразований:
![]()
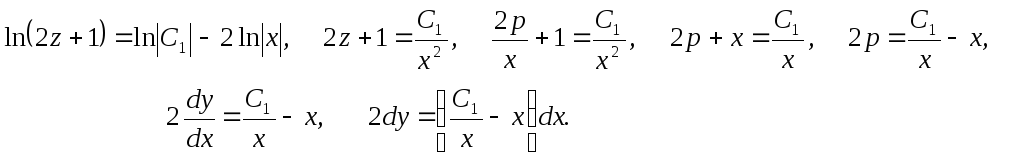
Интегрируя, находим
![]() .
.
Пример 5.Решить уравнение x3 y'' + x2y' =1 (x0).
Положим
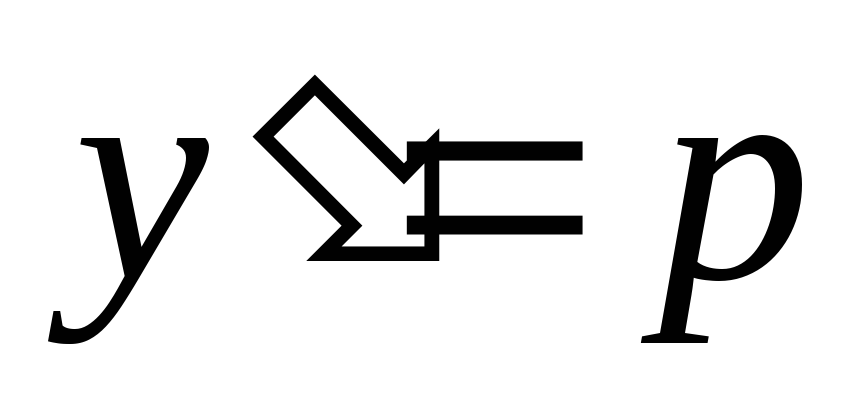 ,
тогда
,
тогда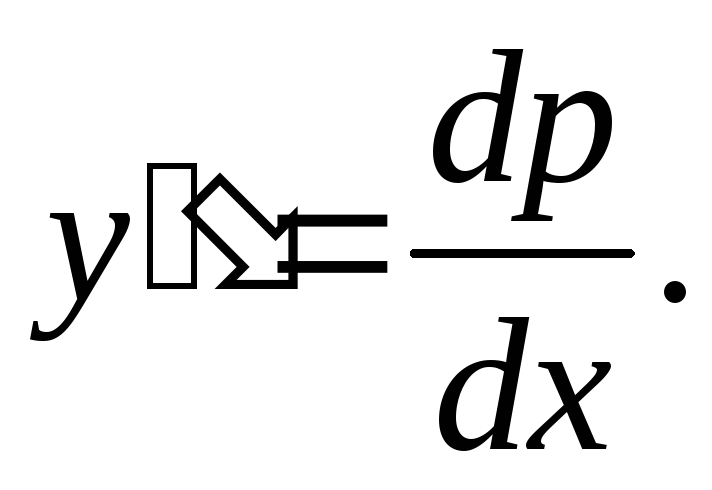 Уравнение примет вид:
Уравнение примет вид:
![]() или
или![]() .
.
Это уравнение линейное
![]() .
.
Цепочка преобразований:
![]() .
Отсюда
.
Отсюда
получаем два уравнения: 1)
![]() .
.
![]() Зная
Зная![]() и
и![]() ,
находим
,
находим![]()
Далее,
![]()
Уравнение вида
|
|
(6.10) |
не содержит явным образом независимого
переменного
![]() .
.
Полагая здесь
![]() и
и![]() ,
,
получим дифференциальное уравнение
первого порядка
![]() ,
где роль независимой переменной играет
,
где роль независимой переменной играет![]() .
Интегрируя его, находим
.
Интегрируя его, находим![]() .
.
Подставляя это значение в соотношение
![]() ,
получаем дифференциальное уравнение
первого порядка для функции
,
получаем дифференциальное уравнение
первого порядка для функции![]() от
от![]() :
:![]() .
.
Разделяя переменные, находим:
![]() .
.
Интегрируя это уравнение, получим общий интеграл исходного уравнения:
![]() .
.
Пример 6. Решить уравнение![]() .
.
![]() .
Подставляем в исходное уравнение:
.
Подставляем в исходное уравнение:![]() .(Учитываем:
.(Учитываем:![]() ,
т.е.
,
т.е.![]() ).
).
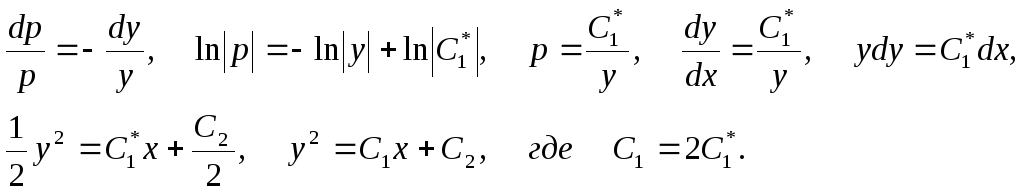
Пример 7.Решить
уравнение
![]() .
.
![]() .
Подставляем в исходное уравнение:
.
Подставляем в исходное уравнение:
![]()
Отсюда: 1)
![]() ,т.е.
,т.е.
![]() .
.
2)
![]() .
Цепочка преобразований:
.
Цепочка преобразований:![]()
![]() ,
,
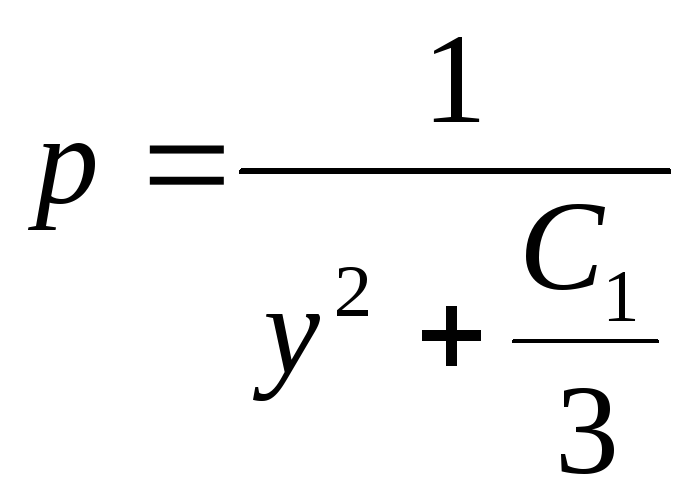 ,
,
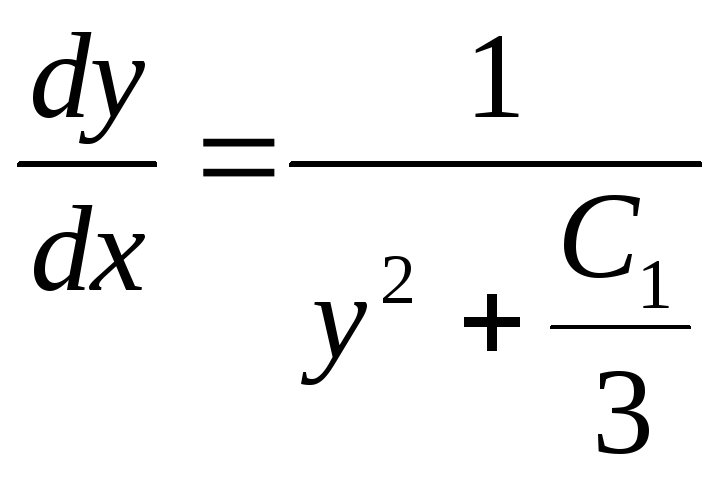 ,
,![]() ,
,
![]() ,
,
![]() .
.
Пример 8.Решить
уравнение
![]() .
.
![]()
![]()
Цепочка
преобразований:
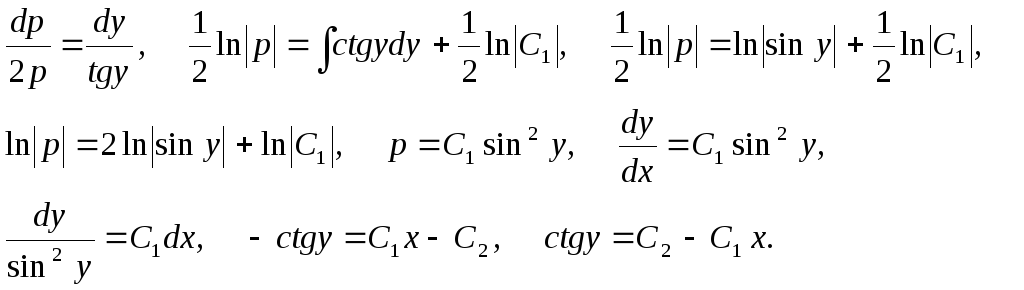
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами содержат у,у', у''в первой степени и коэффициенты при них – постоянные величины
|
y'' + py' + qy =0. |
(7.1) |
Определение 1.Два частных
решения![]() и
и![]() уравнения
(7.1) образуют фундаментальную систему
решений, если для любого
уравнения
(7.1) образуют фундаментальную систему
решений, если для любого![]()

 y1(x)
y2(x)
y1(x)
y2(x)
W(x) = 0 (7.2)
y'1(x) y'2(x)
Определитель
![]() называют
определителем Вронского, или вронскианом
решений
называют
определителем Вронского, или вронскианом
решений![]() и
и![]() .
.
Теорема о структуре общего решения
Если два частных решения![]() и
и![]() линейного однородного дифференциального
уравнения второго порядка с постоянными
коэффициентами образуют фундаментальную
систему, то общее решение этого уравнения
имеет вид
линейного однородного дифференциального
уравнения второго порядка с постоянными
коэффициентами образуют фундаментальную
систему, то общее решение этого уравнения
имеет вид
|
|
(7.3) |
где
![]() и
и![]() -
произвольные постоянные.
-
произвольные постоянные.
Выражение
![]() называется линейной комбинацией
функций
называется линейной комбинацией
функций![]() и
и![]() .
.
Доказательство.Докажем сначала, что функция (7.3) является решением уравнения (7.1). Для этого подставим в уравнение (7.1) вместо у линейную комбинацию и докажем, что оно превращается в тождество:
(C1y1 + C 2y2) ''+ p(C 1y1 + C 2y2) ' + q(C 1y1+ C 2y2) = C1y1'' + C2y2'' + pC1y1' + pC2y2' + +qC1y1+ qC2y2=C1(y1'' + py1' + qy1)+ C2(y2'' + py2' + qy2).
Так как
![]() и
и![]() являются решениями уравнения (7.1):
являются решениями уравнения (7.1):
y1'' + py1' + qy1 =0 и y2'' + py2' + qy2 =0,
то при любых значениях
![]() и
и![]() получаем тождество:
получаем тождество:
![]() .
.
А это значит, что функция (7.3) является решением уравнения (7.1).
Теперь докажем, что формула (7.3) представляет общее решение уравнения (7.1). Для этого достаточно показать, то из него можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям (6.5).
Пусть (x)–какое-либо частное решение уравнения (7.1) и х0– некоторое число из области определения этого решения. Обозначим(х0) =у0, '(х0)=у0'.Отсюда следует, что решениеу=(х) удовлетворяет начальным условиям(х0, у0, у0' ).Покажем, что оно может быть получено из общего решения (7.3) надлежащим выбором постоянныхС1 и С2.
Подставляя начальные условия в равенства
у = С1у1(х)+ С2у2(х),
у' = С1у1'(х) + С2у2'(х),
получим
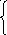 С1у1(х0)+ С2у2(х0)=
у0
(7.4)
С1у1(х0)+ С2у2(х0)=
у0
(7.4)
С1у1'(х0)+ С2у2'(х0)= у0'
Равенства (7.4) представляют собой систему уравнений с неизвестными С1 и С2, причём определитель этой системы
 у1(х0)
у2(х0)
у1(х0)
у2(х0)
W(x0)=
у1' (х0) у2' (х0)
является определителем Вронского для функций у1(х) иу2(х) прих=х0. Так как, по условию, частные решенияу1(х)и у2(х) образуют фундаментальную систему, тоW(х0)0 при любом действительном значениих0. Поэтому система (7.4) имеет единственное решение:
 у0 у2(х0)
y1(x0)
y0
у0 у2(х0)
y1(x0)
y0
С10 = С20 =
у0' у2'(х0) , y1 '(x0) y0'
W(x0) W(x0)
Таким образом, существует частное решение
у = С10у1 + С20у2, (7.3а)
удовлетворяющее начальным условиям (6.5), причём в силу единственности оно совпадает с решением (х).
Этот вывод основывается на теореме Коши, которая для линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами (7.1) формулируется следующим образом.
Теорема Коши: При любых начальных данных (х0; у0; у0') задача Коши имеет, причём единственное, решение, то есть при любых начальных данныхх0, у0, у0'существует, причём единственное, решение уравнения (7.1), удовлетворяющее начальным условиям (6.5):у0(х0) = у0, у'(х0)= у0'.
