
- •1. Основные понятия и определения теории дифференциальных уравнений
- •2. Дифференциальные уравнения первого порядка с разделяющимися переменными
- • Заменив y' на , а затем, умножив все члены наdx, получим
- •3. Однородные дифференциальные уравнения первого порядка
- •Определение 1.Функция f(X,y) называется однородной функцией n-ого измерения (n-ой степени) относительно переменных X и y,если при любом t справедливо тождество
- •Пример 1.Решить уравнение .
- •4. Линейные дифференциальные уравнения первого порядка Линейное дифференциальное уравнение первого порядка имеет вид
- •5. Уравнения в полных дифференциалах
- •6. Уравнения второго порядка, допускающие понижение порядка
- •Уравнение вида
- •Теорема о структуре общего решения
3. Однородные дифференциальные уравнения первого порядка
Понятие однородного дифференциального уравнения первого порядка связано с однородными функциями.
Определение 1.Функция f(X,y) называется однородной функцией n-ого измерения (n-ой степени) относительно переменных X и y,если при любом t справедливо тождество
|
|
(3.1) |
Например, функция
![]() -
однородная функция первого измерения,
так как
-
однородная функция первого измерения,
так как
![]() ;
;
![]() - однородная функция третьего измерения
, так как
- однородная функция третьего измерения
, так как
![]() ;
;
![]() - однородная функция нулевого измерения,
так как
- однородная функция нулевого измерения,
так как
![]() ,
т.е.
,
т.е.![]() .
.
Определение 2.Дифференциальное уравнение первого порядкаy' = f(x,y) называется однородным, если функцияf(x,y) есть однородная функция нулевого измерения относительноx иy, или, как говорят,f(x,y) – однородная функция степени нуль.
Его можно представить в виде
|
P (x, y) dx + Q (x, y) dy = 0, |
(3.2) |
где P(x,y) иQ(x,y) – однородные функции одинакового измерения: отношение двух однородных функций одного и того же измерения является однородной функцией нулевого измерения (см. третий из приведенных выше примеров).
Возможна следующая форма записи уравнения (3.2):
|
|
(3.3) |
что позволяет определить однородное уравнение как такое дифференциальное, которое можно преобразовать к виду (3.3).
Замена
![]() приводит однородное уравнение к
уравнению с разделяющимися переменными.
Действительно, после подстановкиу
= xzполучим
приводит однородное уравнение к
уравнению с разделяющимися переменными.
Действительно, после подстановкиу
= xzполучим![]() ,
,![]() Разделяя переменные и интегрируя,
найдем:
Разделяя переменные и интегрируя,
найдем:
![]()
![]() ,
,
![]()
Пример 1.Решить уравнение .
Полагаем у = zx,
![]() Подставляем
эти выраженияy иdyв данное уравнение:
Подставляем
эти выраженияy иdyв данное уравнение:![]() или
или![]() Разделяем переменные:
Разделяем переменные:![]() и интегрируем:
и интегрируем:![]() ,
,![]()
Заменяя zна![]() ,
получим
,
получим![]() .
.
Пример 2. Найти общее решение
уравнения![]() .
.
В данном уравнении P
(x,y)
=x2-2y2,Q(x,y)
=2xy– однородные
функции второго измерения, следовательно,
данное уравнение является однородным.
Его можно представить в виде![]() и решать так же, как и представленное
выше. Но используем другую форму записи.
Положимy = zx,
откудаdy = zdx
+ xdz. Подставляя эти
выражения в исходное уравнение, будем
иметь
и решать так же, как и представленное
выше. Но используем другую форму записи.
Положимy = zx,
откудаdy = zdx
+ xdz. Подставляя эти
выражения в исходное уравнение, будем
иметь
![]() ,
,
то есть
![]()
![]()
или
dx+2zxdz = 0.
Разделяем переменные, считая
![]()
![]() .
.
Интегрируем почленно это уравнение
![]() ,
откуда
,
откуда![]()
то есть
![]() .
Возвращаясь к прежней функции
.
Возвращаясь к прежней функции![]() находим общее решение
находим общее решение![]()
Пример 3. Найти общее
решение уравнения![]() .
.
Цепочка преобразований:
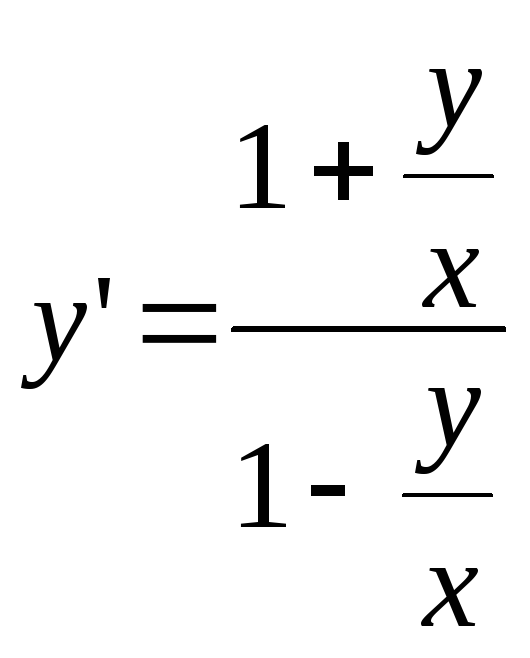 ,y = zx,
,y = zx,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Лекция 8.
4. Линейные дифференциальные уравнения первого порядка Линейное дифференциальное уравнение первого порядка имеет вид
|
|
(4.1) |
где
![]() ,
,![]() ,c(x) –
непрерывные функции.
,c(x) –
непрерывные функции.
Если![]() ,
то уравнение (4.1) можно записать в
приведённом виде
,
то уравнение (4.1) можно записать в
приведённом виде
|
|
(4.1a) |
Здесь
![]() – свободный член, называемый также
правой частью уравнения. В этом виде
будем рассматривать линейное уравнение
в дальнейшем.
– свободный член, называемый также
правой частью уравнения. В этом виде
будем рассматривать линейное уравнение
в дальнейшем.
Если
![]() 0,
то уравнение (4.1а) называется линейным
неоднородным. Если же
0,
то уравнение (4.1а) называется линейным
неоднородным. Если же![]() 0, то уравнение принимает вид
0, то уравнение принимает вид
|
|
(4.2) |
и называется линейным однородным.
Название уравнения (4.1а) объясняется
тем, что неизвестная функция y
и её производная![]() входят в него линейно, т.е. в первой
степени.
входят в него линейно, т.е. в первой
степени.
В линейном однородном уравнении
переменные разделяются. Переписав его
в виде
![]() откуда
откуда![]() и интегрируя, получаем:
и интегрируя, получаем:![]() ,т.е.
,т.е.
|
|
(4.3) |
При делении на
![]() теряем решение
теряем решение![]() .
Однако оно может быть включено в найденное
семейство решений (4.3), если считать, чтоСможет принимать и значение 0.
.
Однако оно может быть включено в найденное
семейство решений (4.3), если считать, чтоСможет принимать и значение 0.
Существует несколько методов решения уравнения (4.1а). Согласно методу Бернулли, решение ищется в виде произведения двух функций отх:
|
|
(4.4) |
Одна из этих функций может быть выбрана произвольно, так как лишь произведение uv должно удовлетворять исходному уравнению, другая определяется на основании уравнения (4.1а).
Дифференцируя обе части равенства
(4.4), находим
![]() .
.
Подставляя полученное выражение
производной
![]() ,
а также значениеу
в уравнение (4.1а), получаем
,
а также значениеу
в уравнение (4.1а), получаем![]() ,
или
,
или
|
|
(4.5) |
Так как одну из неизвестных функций можем выбрать произвольно, выберем функцию u так, чтобы
|
|
(4.6) |
т.е. в качестве функции vвозьмём решение однородного линейного уравнения (4.6):
|
|
(4.3а) |
Ввиду произвольности в выборе v,мы можем не учитывать произвольную постояннуюС (точнее – можем приравнять её нулю). Подставляя найденное значениеv(x) в уравнение (4.5), получим, учитывая (4.6):
|
|
(4.7) |
откуда
|
|
(4.8) |
(Здесь Cписать обязательно, иначе получится не общее, а частное решение).
Таким образом, видим, что в результате используемой подстановки (4.4) уравнение (4.1а) сводится к двум уравнениям с разделяющимися переменными (4.6) и (4.7).
Подставляя
![]() иv(x) в
формулу (4.4), окончательно получаем
иv(x) в
формулу (4.4), окончательно получаем
![]() ,
,
или
|
|
(4.9) |
Пример 1.Найти общее решение
уравнения![]()
Положим
![]() ,
тогда
,
тогда![]() .
Подставляя выражения
.
Подставляя выражения![]() и
и![]() в
исходное уравнение, получим
в
исходное уравнение, получим![]() или
или![]() (*)
(*)
Приравняем нулю коэффициент при
![]() :
:![]()
Разделяя переменные в полученном
уравнении, имеем
![]()
![]()
![]() (произвольную постояннуюC
не пишем), отсюдаv=x.
Найденное значениеvподставляем в уравнение (*):
(произвольную постояннуюC
не пишем), отсюдаv=x.
Найденное значениеvподставляем в уравнение (*):
![]() ,
,![]() ,
,![]() .
.
Следовательно,
![]() общее
решение исходного уравнения.
общее
решение исходного уравнения.
Отметим, что уравнение (*) можно было записать в эквивалентном виде:
![]() .
.
Произвольно выбирая функцию u,
а неv, мы могли полагать![]() .
Этот путь решения отличается от
рассмотренного только заменойvнаu(и, следовательно,uнаv),
так что окончательное значениеуоказывается тем же самым.
.
Этот путь решения отличается от
рассмотренного только заменойvнаu(и, следовательно,uнаv),
так что окончательное значениеуоказывается тем же самым.
На основании изложенного выше получаем алгоритм решения линейного дифференциального уравнения первого порядка.
Приводим рассматриваемое уравнение к виду
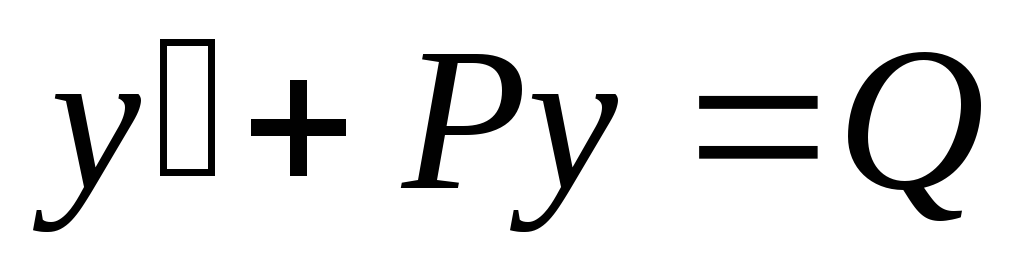 .
.Используя подстановку
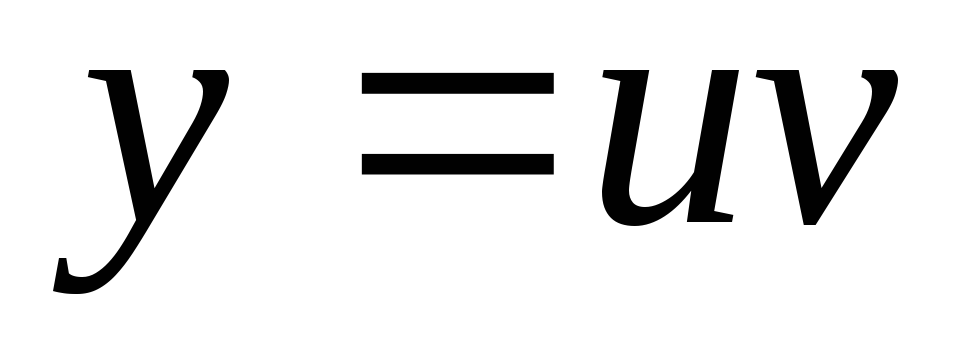 ,
находим
,
находим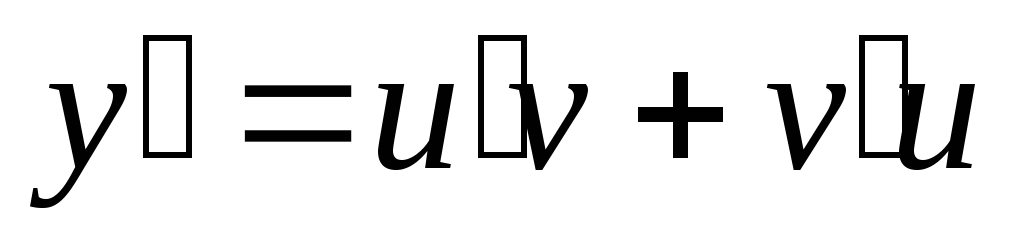 и
подставляем эти выражения в уравнение.
и
подставляем эти выражения в уравнение.Группируем члены уравнения, выносим одну из функций uилиvза скобки. Находим вторую функцию, приравняв выражение в скобках нулю и решив полученное уравнение.
Подставляем найденную функцию в оставшееся выражение и находим вторую функцию.
Записываем общее решение, подставив выражения для найденных функций u иvв равенство
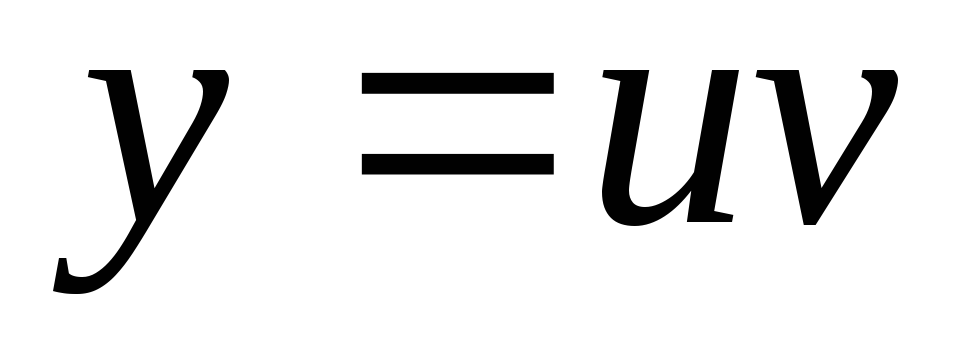 .
.Если требуется найти частное решение, то определяем Сиз начальных условий и подставляем в общее решение.
Отметим далее, что иногда уравнение первого порядка становится линейным, если усчитать независимой переменной, аx– зависимой, т.е. поменять ролиx иy. Это можно сделать при условии, чтоxиdxвходят в уравнение линейно.
Пример 2. Решить уравнение
![]() .
.
По виду это уравнение не является линейным относительно функции у.
Однако если рассматривать xкак функцию оту, то, учитывая, что![]() ,его
можно привести к виду
,его
можно привести к виду
|
|
(4.1 б) |
Заменив
![]() на
на![]() ,получим
,получим![]() или
или![]() .
Разделив обе части последнего уравнения
на произведениеydy,
приведем его к виду
.
Разделив обе части последнего уравнения
на произведениеydy,
приведем его к виду
![]() , или
, или![]() .
(**)
.
(**)
Здесь P(y)=![]() ,
,![]() .
Это линейное уравнение относительноx. Полагаем
.
Это линейное уравнение относительноx. Полагаем![]() ,
,![]() .
Подставляя эти выражения в (**), получаем
.
Подставляя эти выражения в (**), получаем
![]() или
или![]() .
.
Выберем vтак, чтобы![]() ,
,![]() ,
откуда
,
откуда![]() ;
;![]() .
Далее имеем
.
Далее имеем![]() ,
,![]() ,
,![]() .
.
Т.к.
![]() ,
то приходим к общему решению данного
уравнения в виде
,
то приходим к общему решению данного
уравнения в виде
![]() .
.
Отметим, что в уравнение (4.1а) P(x) иQ (x) могут входить не только в виде функций от x, но и констант:P=a,Q=b. Линейное уравнение
|
|
(4.10) |
можно решать и с помощью подстановки y=uv и разделением переменных:
![]() ;
;![]() .
.
Отсюда
![]() ;
;![]() ;
;![]() ;
где
;
где![]() .
Освобождаясь от логарифма, получаем
общее решение уравнения
.
Освобождаясь от логарифма, получаем
общее решение уравнения
![]() (здесь
(здесь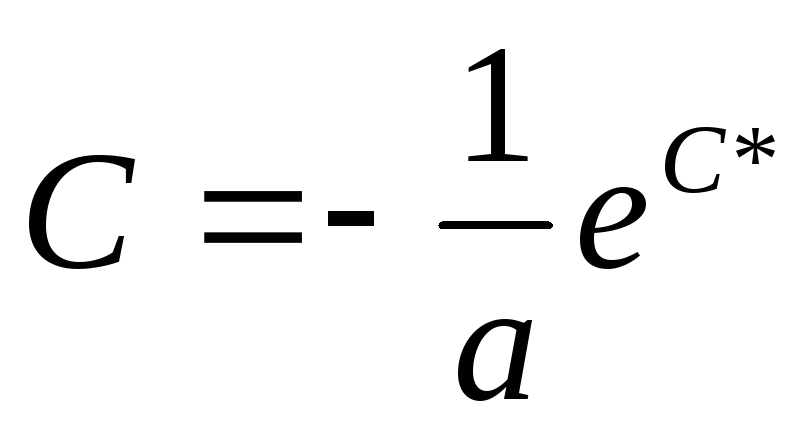 ).
).
При b=0 приходим к решению уравнения
|
|
(4.10а) |
в виде
|
|
(4.11) |
(см. уравнение показательного роста
(2.4) при
![]() ).
).
Применим далее для интегрирования неоднородного линейного уравнения (4.1а) метод вариации произвольной постоянной (метод Лагранжа).
Сначала интегрируем соответствующее однородное уравнение (4.2). Как указано выше, его решение имеет вид (4.3). Будем считать сомножитель Св (4.3) функцией отх, т.е. по существу делаем замену переменной
|
|
(4.3а) |
где C(x)-новая
неизвестная функцияx.
Подставляя производную![]() в исходное неоднородное уравнение
(4.1а), получим:
в исходное неоднородное уравнение
(4.1а), получим:![]()
![]() ,
или
,
или
|
|
(4.12) |
откуда, интегрируя, находим
|
|
(4.13) |
где С1-постоянная. Следовательно,
|
|
(4.14) |
Отметим, что согласно (4.14) (см. также (4.9)), общее решение неоднородного линейного уравнения равно сумме общего решения соответствующего однородного уравнения (4.3) и частного решения неоднородного уравнения, определяемого вторым слагаемым, входящим в (4.14) (и в (4.9)).
При решении конкретных уравнений следует повторять приведённые выше выкладки, а не использовать громоздкую формулу (4.14).
Применим метод Лагранжа к уравнению, рассмотренному в примере 1:
![]() .
.
Интегрируем соответствующее однородное
уравнение
![]() .
.
Разделяя переменные, получаем
![]() и далее
и далее![]() .
Решение выражения формулойy
= Cx. Решение исходного
уравнения ищем в видеy
= C(x)x.
Подставив это выражение в заданное
уравнение, получим
.
Решение выражения формулойy
= Cx. Решение исходного
уравнения ищем в видеy
= C(x)x.
Подставив это выражение в заданное
уравнение, получим![]() ;
;![]() ;
;![]() ,
,![]() .
Общее решение исходного уравнения имеет
вид
.
Общее решение исходного уравнения имеет
вид
![]() .
.
В заключение отметим, что к линейному уравнению приводится уравнение Бернулли
|
|
(4.15) |
которое можно записать в виде
|
|
(4.15а) |
Заменой
![]() оно приводится к линейному уравнению:
оно приводится к линейному уравнению:
![]() ,
,![]() ,
,![]() .
.
Уравнения Бернулли также решаются изложенными выше методами.
Пример 3. Найти общее
решения уравнения![]() .
.
Цепочка преобразований:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
