
- •1. Основные понятия и определения теории дифференциальных уравнений
- •2. Дифференциальные уравнения первого порядка с разделяющимися переменными
- • Заменив y' на , а затем, умножив все члены наdx, получим
- •3. Однородные дифференциальные уравнения первого порядка
- •Определение 1.Функция f(X,y) называется однородной функцией n-ого измерения (n-ой степени) относительно переменных X и y,если при любом t справедливо тождество
- •Пример 1.Решить уравнение .
- •4. Линейные дифференциальные уравнения первого порядка Линейное дифференциальное уравнение первого порядка имеет вид
- •5. Уравнения в полных дифференциалах
- •6. Уравнения второго порядка, допускающие понижение порядка
- •Уравнение вида
- •Теорема о структуре общего решения
5. Уравнения в полных дифференциалах
Уравнение
|
|
(5.1) |
называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции u(x,y):
![]() .
.
Для того чтобы уравнение (5.1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы
|
|
(5.2) |
Если известна функция, полным дифференциалом которой является левая часть уравнения (5.1), то все решения этого уравнения удовлетворяют условию u(x,y)=C, гдеС - произвольная постоянная.
Чтобы найти функцию u(x,y), воспользуемся равенствами :
|
|
(5.3) |
Интегрируя первое из этих равенств по x, считаемy постоянным, и поэтому константа интегрирования может зависеть оту:
|
|
(5.4) |
где
![]() произвольная дифференцируемая функция,F(x,y)-
первообразная отP(x,y).
Подберем функцию
произвольная дифференцируемая функция,F(x,y)-
первообразная отP(x,y).
Подберем функцию![]() так, чтобы удовлетворялось второе из
соотношений (5.3). Для этого продифференцируем
(5.4) поу и результат приравняем к
так, чтобы удовлетворялось второе из
соотношений (5.3). Для этого продифференцируем
(5.4) поу и результат приравняем к![]() .
Таким образом, получим уравнение для
определения функции
.
Таким образом, получим уравнение для
определения функции![]() :
:
|
|
(5.5) |
Из (5.5) определяем
![]() и, интегрируя, находим
и, интегрируя, находим![]() .
Подставляя эту найденную функцию в
соотношение (5.4), получаем искомую функциюu(x,y).
.
Подставляя эту найденную функцию в
соотношение (5.4), получаем искомую функциюu(x,y).
Пример 1. Решить уравнение (2xy+3y2)dx + (x2+6xy-3y2)dy = 0.
В данном случае
![]() ,
,![]() .
.
![]() ,
,![]() .
.
Следовательно,
![]() ,
и левая часть данного уравнения является
полным дифференциалом некоторой функции
,
и левая часть данного уравнения является
полным дифференциалом некоторой функции![]() .
Имеем
.
Имеем
![]() ,
,![]() .
.
Из первого уравнения находим
![]() .
.
Для определения функции
![]() дифференцируем полученное равенство
поуи приравниваем выражению
дифференцируем полученное равенство
поуи приравниваем выражению![]()
![]() ,
,
т.е.
![]() .
Отсюда
.
Отсюда![]() .
Поэтому
.
Поэтому![]() .
Общее решение записывается в виде
.
Общее решение записывается в виде
![]()
Пример 2. Решить уравнение![]() .
.
Это уравнение в полных дифференциалах, т.к.
![]() .
.
Функцию u(x,y)
найдем из уравнений![]() .
Интегрируя второе из этих уравнений поу, считаяхпостоянным, имеем:
.
Интегрируя второе из этих уравнений поу, считаяхпостоянным, имеем:![]() где
где![]() − произвольная дифференцируемая
функция.
− произвольная дифференцируемая
функция.![]() .
Следовательно,
.
Следовательно,![]()
![]() .
.
Пусть левая часть уравнения (5.1) не есть
полный дифференциал. Иногда удается
подобрать такую функцию
![]() ,
после умножения на которую всех членов
уравнения его левая часть становится
полным дифференциалом. Общее решение
полученного таким образом уравнения
совпадает с общим решением первоначального
уравнения. Функция
,
после умножения на которую всех членов
уравнения его левая часть становится
полным дифференциалом. Общее решение
полученного таким образом уравнения
совпадает с общим решением первоначального
уравнения. Функция![]() называетсяинтегрирующим множителемуравнения
(5.1).
называетсяинтегрирующим множителемуравнения
(5.1).
Итак, умножим обе части уравнения (5.1)
на
![]()
|
|
(5.1а) |
Для того чтобы это уравнение было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение
![]() ,
,
т.е.
![]() .
.
Таким образом, интегрирующий множитель есть решение уравнения
|
|
(5.6) |
В некоторых частных случаях уравнение (5.6) упрощается и интегрирующий множитель для уравнения (5.1) легко найти.
Если уравнение (5.1)имеет интегрирующий множитель, зависящий только от х , т.е.
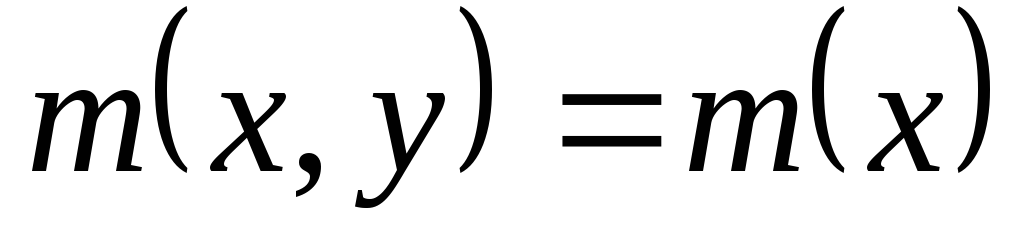 ,
то из уравнения (5.6)имеем
,
то из уравнения (5.6)имеем
|
|
(5.7) |
Если уравнение (5.1) допускает интегрирующий множитель как функцию одной переменной у, т.е.
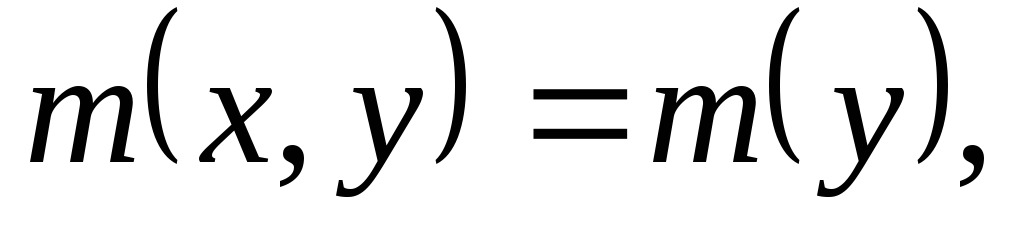 то
то
|
|
(5.8)
|
Пример 3. Решить уравнение![]()
Выясним, имеет ли данное уравнение
интегрирующий множитель как функцию
одной переменой. Вычислим
![]() .
.
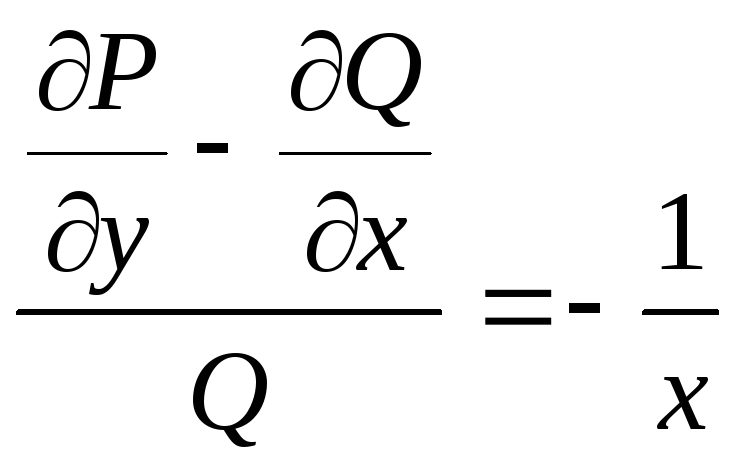 ,т.е.
является функцией, зависящий только отх. Следовательно, интегрирующий
множитель находим из уравнения
,т.е.
является функцией, зависящий только отх. Следовательно, интегрирующий
множитель находим из уравнения![]() ,
т.е.
,
т.е.![]() .
.
Умножая исходное уравнение на
![]() ,
получим уравнение в полных дифференциалах:
,
получим уравнение в полных дифференциалах:
![]() .
.
Записав его в виде
![]()
![]() ,
,
имеем
![]()
Лекция 9.

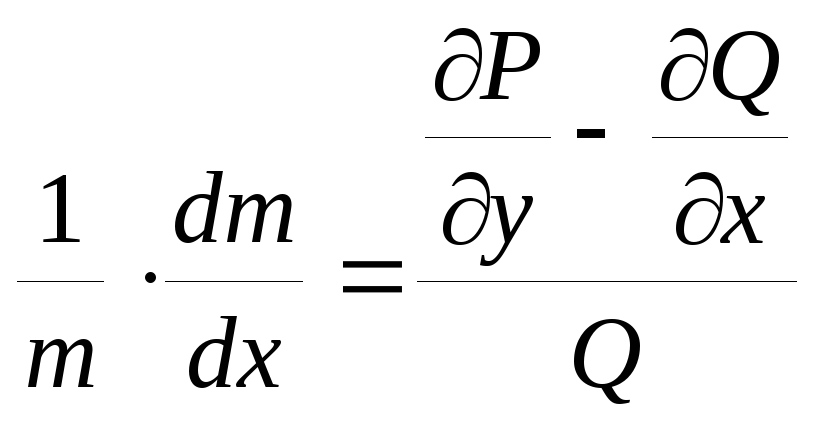 .
.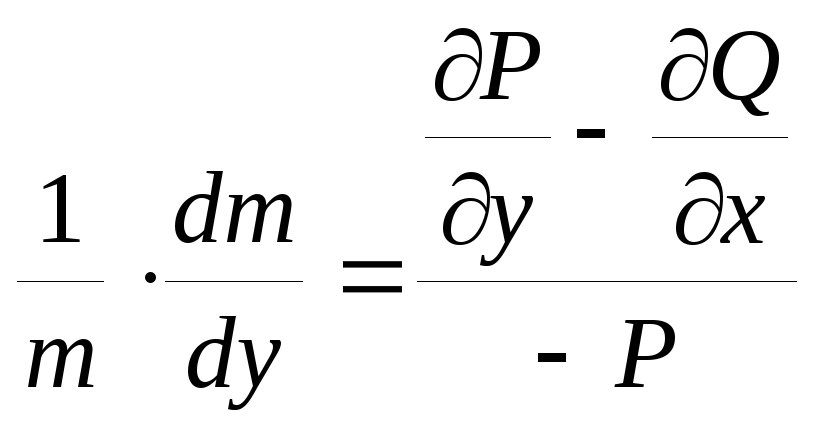 .
.