110

Лекция 10.

8. Решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами

Для нахождения общего решения уравнения (7.1), согласно доказанной на предыдущей лекции теореме, достаточно найти два его частных решения, образующих фундаментальную систему, т.е. два линейно независимых частных решения. Будем искать решения (по Эйлеру) в виде

,

(8.1)

где − действительное или комплексное число, подлежащее определению. Подставляя функцию (8.1) и ее производные,в уравнение (7.1), получим

, т.е..

Выражение как показательная функция ни при каких значениях х не равна нулю. Следовательно,

.

(8.2)

Уравнение (8.2) называется характеристическимдля данного дифференциального уравнения (7.1). Чтобы получить его, достаточно заменить в (7.1)соответственно наи 1.

Характеристическое уравнение есть квадратное уравнение, имеющее два корня: ,. Решив его, найдеми, а следовательно и частные решения уравнения (7.1):

,.

(8.3)

При решении характеристического уравнения возможны следующие три случая.

I. Корни характеристического уравнения действительные и различные:

В этом случае частные решения иобразуют фундаментальную систему решений, так как их вронскиан

Следовательно, в этом случае общее решение уравнения (7.1) имеет вид

(8.4)

Пример 1. Найти общее решение уравнения

 Напишем характеристическое уравнение данного дифференциального уравнения:

Это уравнение имеет корни и. По формуле (8.4) получаем общее решение:

II.Корни характеристического уравнения действительные и равные:

Одно частное решение получается на основании предыдущих рассуждений. Нужно найти второе частное решение, линейно независимое с первым. Будем искать второе частное решение в виде

,

(8.5)

где - неизвестная функция, подлежащая определению. Дифференцируя (8.5), находим

Подставляя ив левую часть уравнения (7.1),получаем

Так как -кратный корень характеристического уравнения , то

Кроме того, или. Следовательно, для того чтобы найти функциюнадо решить уравнениеИнтегрируя, получаем

где и- произвольное постоянные. В частности, можно положить,.

Тогда Таким образом,

(8.5а)

- второе частное решение уравнения (7.1). Решения илинейно независимы. Поэтому общим решением будет функция

.

(8.6)

Пример 2. Найти общее решение уравнения.

 Характеристическое уравнение имеет вид:

Его корни -вещественные и равные. Следовательно, общее решение данного дифференциального уравнения имеет вид:



III. Корни характеристического уравнения комплексные:

,.

В этом случае частные решения имеют вид:

.

Согласно формуле Эйлера

,

.

Поэтому

.

Чтобы заменить комплексные решения действительными, рассмотрим функции

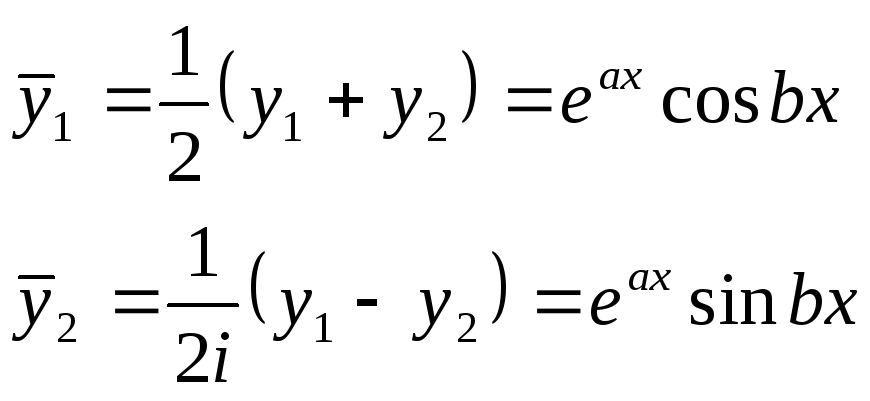
Так как иявляются линейными комбинациями частных решенийи, т.е. имеют вид (7.3),то они сами являются решениями уравнения (7.1). Вычисляя вронскиан, можно убедиться, что они составляют фундаментальную систему:

.

Таким образом, общее решение уравнения (7.1) в случае комплексных корней характеристического уравнения имеет вид

,

или (8.7)

Пример 3. Решить уравнение.

• Корни характеристического уравнения

комплексные: и. Здесь. Поэтому общим решением является функция

.