
- •8. Решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •Пример 4.Найти частное решение уравнения , удовлетворяющее начальным условиями. Составляем характеристическое уравнение
- •9. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •10. Методы нахождения частных решений неоднородных линейных уравнений второго порядка с постоянными коэффициентами
- •Пример 1. Найти частное решение уравнения.
- •Пример 2. Найти частное решение уравнения .
- •Пример 7. Пусть .
- •D Соответствующее однородное уравнение будет .
- •Решая характеристическое уравнение , находим корни
- •. Следовательно, общее решение однородного уравнения есть
- •11. Системы дифференциальных уравнений
- •Метод нахождения интегрируемых комбинаций
- •Метод исключения неизвестных
- •Понятие о системах линейных дифференциальных уравнений с постоянными коэффициентами
- •Учебное издание Романов Юрий Иванович
- •115998, Москва, ул. Садовническя, 33
10. Методы нахождения частных решений неоднородных линейных уравнений второго порядка с постоянными коэффициентами
В общем случае задача нахождения частного решения неоднородного уравнения (9.1) является сложной. Можно получить решение методом вариации постоянных, если известно общее решение соответствующего однородного уравнения (9.2).
|
|
(10.1) |
Будем искать частное решение неоднородного уравнения в форме (10.1), рассматривая С1 иС2как некоторые искомые функции отх:
|
|
(10.2) |
Продифференцируем это равенство
|
|
(10.3) |
Подберем искомые функции С1(х) иС2(х) так, чтобы выполнялось равенство
|
|
(10.4) |
С учетом этого
дополнительного условия первая
производная
![]() принимает
вид
принимает
вид
![]() .
.
Дифференцируя это равенство, найдем
![]() :
:
![]() .
.
Подставляя
![]() и
и
![]() в уравнение (9.1) и группируя слагаемые,
получаем
в уравнение (9.1) и группируя слагаемые,
получаем
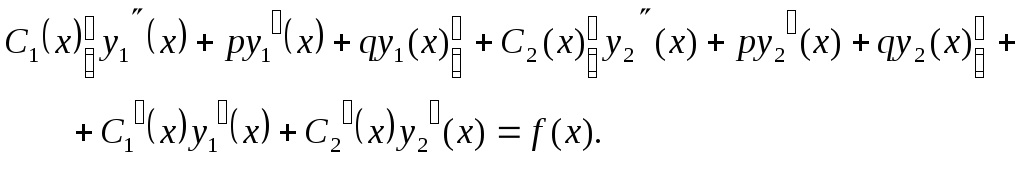
Выражения, стоящие в скобках, равны
нулю, так как
![]() и
и![]() -
решения однородного уравнения.
Следовательно, последнее равенство
принимает вид
-
решения однородного уравнения.
Следовательно, последнее равенство
принимает вид
|
|
(10.5) |
Таким образом, функция (10.2) является решением уравнения (9.1), если функции С1(х) иС2(х) удовлетворяют системе уравнений (10.4) и (10.5):
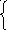
![]() (10.6)
(10.6)
![]() .
.
Эта система имеет единственное решение
относительно
![]() и
и
![]() ,так как ее определителем является
определитель Вронского для линейно
независимых решений
,так как ее определителем является
определитель Вронского для линейно
независимых решений
![]() и
и![]() однородного уравнения (9.2). Согласно
теореме о структуре общего решения
этого уравнения, он не равен нулю. Решая
систему (10.6), находим
однородного уравнения (9.2). Согласно
теореме о структуре общего решения
этого уравнения, он не равен нулю. Решая
систему (10.6), находим
![]() и
и
![]() как
определенные функции отх:
как
определенные функции отх:
![]() ,
,![]() .
.
Интегрируя, найдем
![]() и
и
![]() :
:
![]() ,
,
![]() ,
,
где
![]() и
и![]() − постоянные интегрирования. Подставляя
полученные выражения для
− постоянные интегрирования. Подставляя
полученные выражения для
![]() и
и
![]() в равенство (10.2), получаем искомое
частное решение уравнения (9.1) (при
в равенство (10.2), получаем искомое
частное решение уравнения (9.1) (при![]() ).
).
Пример 1. Найти частное решение уравнения.
Общее решение соответствующего
однородного уравнения
![]() определяется выражением
определяется выражением
![]() .
.
Поэтому частное решение исходного неоднородного уравнения будем искать в виде (варьируем С1 и С2 )
![]() .
.
Система (10.6) для нахождения
![]() и
и
![]() в данном случае записывается так:
в данном случае записывается так:
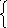
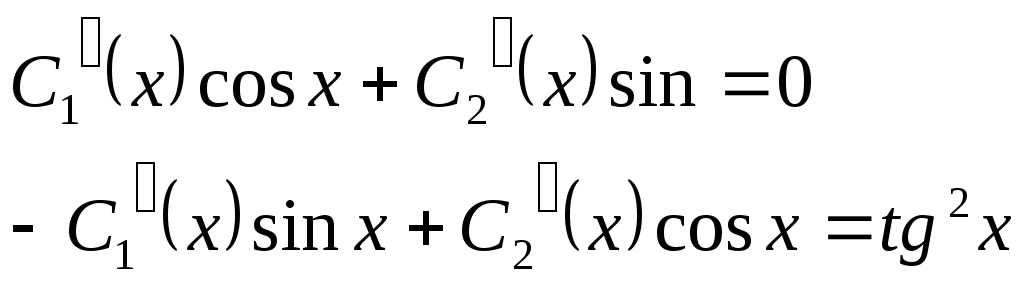 .
.
Отсюда
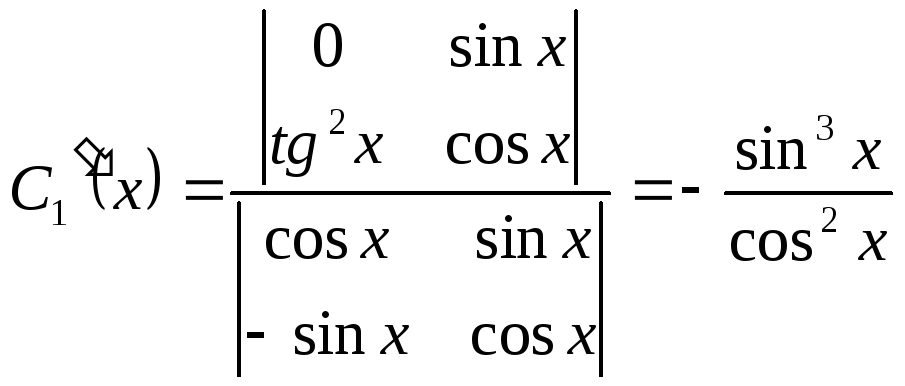 ;
;
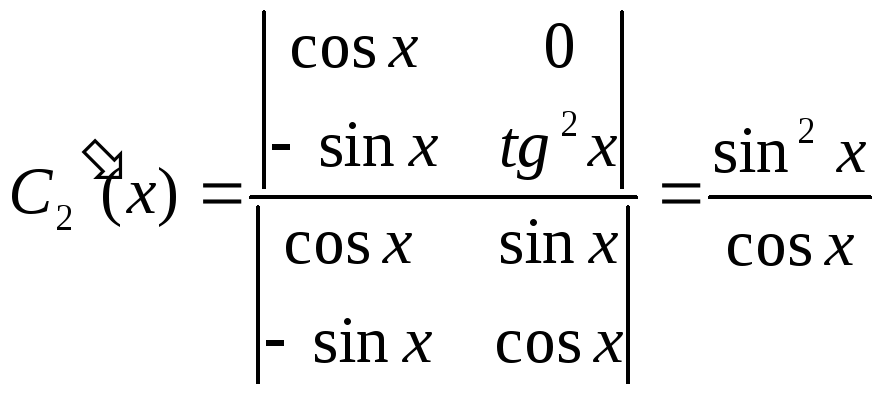 .
.
В
результате интегрирования получаем
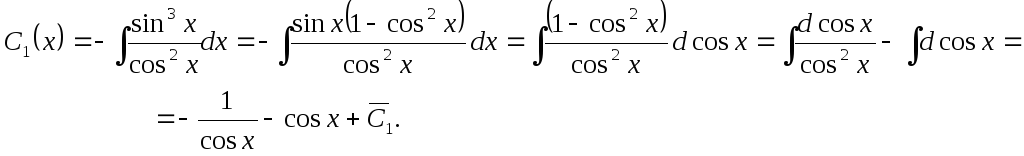
![]() .
.
Подставляя
![]() и
и
![]() в
выражение для у*, произвольные
постоянные не пишем, так как ищем частное
решение
в
выражение для у*, произвольные
постоянные не пишем, так как ищем частное
решение
![]()
Зная общее решение соответствующего однородного уравнения, можем записать общее решение рассмотренного неоднородного уравнения
![]()
Пример 2. Найти частное решение уравнения .
В данном случае
![]() .
Поэтому ищему*в виде
.
Поэтому ищему*в виде![]() .
.
Согласно (10.6), имеем
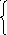
![]()
![]() .
.
Решая систему, находим
![]() ,
,
![]() .
.
Отсюда
![]()
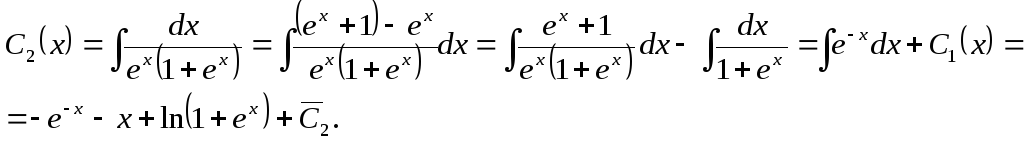
Таким образом, частное решение исходного уравнения имеет вид:
![]()
Если правая часть уравнения (9.1) содержит
многочлен, либо показательную функцию
, либо тригонометрическую функцию
![]() или
или![]() ,
то частное решение может быть найденометодом неопределенных коэффициентов,
не содержащим процесса интегрирования.
,
то частное решение может быть найденометодом неопределенных коэффициентов,
не содержащим процесса интегрирования.
Рассмотрим различные виды правых частей
уравнения (9.1)
![]()
Случай I.Правая часть представляет собой полином, например, второй степени
![]() (10.7)
(10.7)
Если
![]() ,
то частное решениеу* уравнения
(9.1) ищется также в форме квадратного
трехчлена:
,
то частное решениеу* уравнения
(9.1) ищется также в форме квадратного
трехчлена:![]() ,
где
,
где![]() и
и![]() -
неопределенные коэффициенты. Дифференцируя
дваждыy* :
-
неопределенные коэффициенты. Дифференцируя
дваждыy* :![]() ,
,![]() и подставляя эти выражения в уравнение
(9.1), в котором
и подставляя эти выражения в уравнение
(9.1), в котором![]() определяется (10.7), получим:
определяется (10.7), получим:
![]()
или
![]() .
.
Сравнивая коэффициенты при одинаковых степенях xв обеих частях равенства, имеем:
![]()
![]() (10.8)
(10.8)
Так как
![]() ,
то из этой системы для коэффициентов
,
то из этой системы для коэффициентов![]() и
и![]() получаются определенные числовые
значения. Тем самым частное решениеy*
будет вполне определено.
получаются определенные числовые
значения. Тем самым частное решениеy*
будет вполне определено.
Если же
![]() (характеристическое
уравнение имеет простой нулевой корень),
то система(10.8) несовместна. В этом случае
частное решение, полагая, что
(характеристическое
уравнение имеет простой нулевой корень),
то система(10.8) несовместна. В этом случае
частное решение, полагая, что![]() ,
следует искать в форме
,
следует искать в форме![]() .
.
Аналогично обстоит дело, если
![]() есть полином какой-нибудь другой степени,
например,
есть полином какой-нибудь другой степени,
например,![]() или
или![]() .
.
Пример 3.Решить уравнение![]() .
.
Однородное уравнение здесь следующее
![]() .
.
Характеристическое уравнение
![]() имеет корни
имеет корни![]() и
и![]() .
Следовательно, общее решение однородного
уравнения есть
.
Следовательно, общее решение однородного
уравнения есть![]()
Частное решение данного уравнения ищем
в виде
![]() .
.
Находим
![]() ,
,![]() .
.
Подставив эти выражения в исходное уравнение, получим
![]() ,
откуда
,
откуда
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Следовательно,
![]() ,
,![]() ,
,![]() ,
,![]() ,
т.е.
,
т.е.![]() ,
,
а общее решение данного уравнения будет
![]() .
.
Пример 4.Решить уравнение![]() .
.
DИмеем![]() ,
,![]() ,
,![]() ,
,![]() .
.
Так как 0- однократный корень
характеристического уравнения, то
частное решение данного уравнения ищем
в виде
![]() .
Далее решение идет, как в предыдущем
примере:
.
Далее решение идет, как в предыдущем
примере:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]()
Случай II.Правая часть линейного неоднородного уравнения (9.1) есть показательная функция
![]()
![]() .
(10.9)
.
(10.9)
Ищем частное решение также в форме
показательной функции
![]() ,
,
где A-неопределенный
коэффициент, отсюда![]()
![]() .
.
Подставляя
![]() и выражения для
и выражения для![]() и его производных в уравнение (9.1), получим
и его производных в уравнение (9.1), получим
![]() ,
или после сокращения на
,
или после сокращения на![]() :
:
![]() .
(10.10)
.
(10.10)
Если
![]() не является корнем характеристического
уравнения, то
не является корнем характеристического
уравнения, то
![]() и, следовательно,
и, следовательно,![]() .
.
Если число
![]() есть корень характеристического
уравнения, т.е.
есть корень характеристического
уравнения, т.е.![]() ,
то уравнение (10.10) противоречиво и,
следовательно, уравнение (9.1) не имеет
частного решения в форме (10.9).
,
то уравнение (10.10) противоречиво и,
следовательно, уравнение (9.1) не имеет
частного решения в форме (10.9).
В этом
случае, если
![]() есть простой корень характеристического
уравнения (т.е. другой корень отличен
от
есть простой корень характеристического
уравнения (т.е. другой корень отличен
от![]() ),
то частное решение ищется в форме
),
то частное решение ищется в форме![]() .
Если же
.
Если же![]() -двукратный
корень характеристического уравнения,
то частное решение уравнения (9.1) нужно
искать в виде
-двукратный
корень характеристического уравнения,
то частное решение уравнения (9.1) нужно
искать в виде![]() .
.
Пример 5.Пусть![]() .
.
DРешаем уравнение
без правой части :![]() .
Характеристическое уравнение имеет
равные корни
.
Характеристическое уравнение имеет
равные корни![]() ,
и общее решение однородного уравнения:
,
и общее решение однородного уравнения:![]() .
Так как
.
Так как![]() не является корнем характеристического
уравнения, то ищем решение уравнения с
правой частью в следующей форме:
не является корнем характеристического
уравнения, то ищем решение уравнения с
правой частью в следующей форме:![]() ,
где
,
где![]() -неопределенный
коэффициент. Дифференцируя, будем иметь
-неопределенный
коэффициент. Дифференцируя, будем иметь![]() ,
,![]() .
Подставляя эти выражения в исходное
уравнение, получим
.
Подставляя эти выражения в исходное
уравнение, получим
![]() -
-![]() +
+![]() =
=![]() .
Отсюда
.
Отсюда![]() =1.
Итак, частное решение уравнения с правой
частью есть
=1.
Итак, частное решение уравнения с правой
частью есть![]() .
Общее же решение этого уравнения имеет
вид
.
Общее же решение этого уравнения имеет
вид
![]() .
.
Пример 6.Решить уравнение![]() .
.
DКак и в предыдущем
примере,![]() .
Но в данном уравнении
.
Но в данном уравнении![]() -двукратный
корень характеристического уравнения
. Поэтому частное решение ищем в виде :
-двукратный
корень характеристического уравнения
. Поэтому частное решение ищем в виде :![]() .
Далее имеем:
.
Далее имеем:![]() ,
,![]() ,
,![]()
![]() -
-![]()
![]() +
+![]() =
=![]() ,
,![]() =1.
Следовательно,
=1.
Следовательно,![]()
и
![]() .
.
Случай III.Правая часть неоднородного уравнения (9.1) есть тригонометрический
полином
![]() ,
(10.11)
,
(10.11)
где
![]() и
и![]() не нули одновременно.
не нули одновременно.
Ищем частное решение у* этого
уравнения также в форме тригонометрического
полинома![]() (
(![]() и
и![]() -неопределенные
коэффициенты).
-неопределенные
коэффициенты).
Дифференцируя, получим
![]() и
и![]() .
.
Подставляя эти выражения в уравнение
(9.1) и собирая вместе члены с
![]() и
и![]() ,
получим:
,
получим:
![]() .
.
Последнее равенство представляет собой
тождество, и коэффициенты при
![]() и
и![]() в обеих частях этого равенства должны
быть соответственно равны друг другу.
Поэтому
в обеих частях этого равенства должны
быть соответственно равны друг другу.
Поэтому
![]() ,
,![]() .
(10.12)
.
(10.12)
Из этой системы определяются коэффициенты
![]() и
и![]() .
.
Единственный случай, когда система
(10.12) несовместна, это
![]() ,
,
т.е. когда
![]() - корни характеристического уравнения.
Тогда частное решениеу* ищется в
виде
- корни характеристического уравнения.
Тогда частное решениеу* ищется в
виде
![]() .
.
