6. Уравнения второго порядка, допускающие понижение порядка

Дифференциальное уравнение второго порядка в общем случае записывается в виде

F (x, y, y ' ,y'')=0,

(6.1)

или, если это возможно, в разрешённом относительно у''виде

y'' = f(x, y, y' ).

(6.2)

Общее решение

(6.3)

этого уравнения содержит две произвольные постоянные и.

Любая функция

(6.4)

получающаяся из общего решения уравнения (6.2) при определённых значениях постоянных , называется частным решением.

Для дифференциальных уравнений второго порядка задача Коши формулируется следующим образом: найти решение у =y(х) уравнения (6.2), удовлетворяющее начальным условиям

(6.5)

yгдеи– заданные числа.

Сгеометрической точки зрения условия (6.5) означают,

что из семейства интегральных кривых, проходящих

через точку , мы выделяем определённую

интегральную кривую, имеющую

заданный угол наклона .y₀

x₀x

Рассмотрим простейшие случаи, когда уравнение второго порядка решается с помощью квадратур, т. е. применением операций неопределённого интегрирования.

а)y'' = f (x) (6.6)

Полагаем y'=p(x); тогдаy''=p', и уравнение (6.6) примет видp'=f(x), илиdp= f(x)dx. Отсюда

p==F(x) + C₁,

где F(x) -первообразная для функцииf(x). Так какp=y' , тоy' = F(x)+ C_1, илиdy=F(x)dx+C₁dx .

Интегрируя ещё раз, находим общее решение уравнения (6.6)

y=+C₁x +C₂.

Пример 1.Найти общее решение уравненияy'' = cos2x.

 Положим y'=p(x); тогда y'' =p',следовательно,

p'=cos2x или dp=cos 2x dx.

Интегрируя это уравнение, находим

или, т.е..

Интегрируя второй раз, находим искомое общее решение:

,

т.е. 

б)y'' = f(y) (6.7)

Для решения этого уравнения снова полагаем , но теперь мы будем считатьpфункцией оту(а не от).

Тогда .

Относительно вспомогательной функции рполучаем уравнение первого порядка

.

Интегрируя его, найдём ркак функцию отуи произвольной постоянной:

.

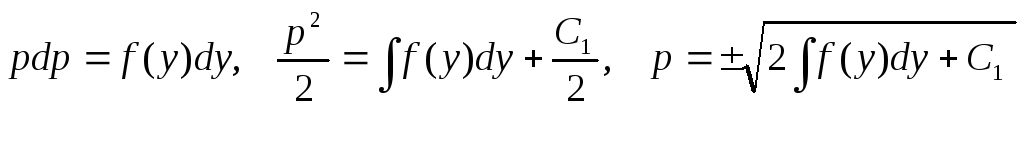Так как , то предыдущее уравнение можно записать так :

.

Далее, разделяя еще раз переменные и интегрируя, окончательно будем иметь

.

Эту формулу общего решения запоминать не следует, нужно усвоить изложенный способ интегрирования.

Пример 2. Проинтегрировать уравнениеу''= -у.

 Цепочка преобразований:



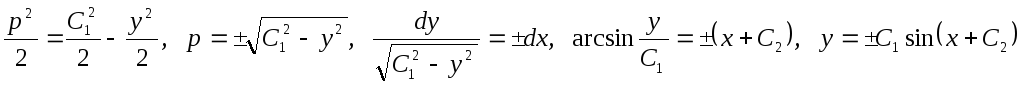
в) y''=f(y' ) (6.8)

Полагаем .

Уравнение (6.8) примет вид .

Разделяя переменные и интегрируя, находим

Определив из полученного уравнения величину путем вторичного интегрирования можно найти.

Пример 3. Проинтегрировать уравнение.

• Цепочка преобразований:

Возвращаясь к переменной , получим

Итак, в рассмотренных простейших случаях удаётся свести дифференциальное уравнение второго порядка к уравнению первого порядка, введя в качестве новой неизвестной функции производную

Переходим к рассмотрению двух видов уравнений, частными случаями которых являются уравнения (6.7) и (6.8).