2. Дифференциальные уравнения первого порядка с разделяющимися переменными

Определение.Дифференциальное уравнение первого порядкаy' =(x, y) называется уравнением с разделяющимися переменными, если его можно представить в виде:

y' = 1(x) 2(y).

(2.1)

В частности, при ₂(y)1 имеем простейшее уравнение

y' =(x).

(2.1а)

Из теории неопределённого интеграла следует, что решение этого уравнения может быть записано следующим образом:

y =+C.

(2.2)

Очевидно, если число аявляется решением уравнения₂(y) = 0, то функцияy=a(постоянная) является решением уравнения (2.1). Для техy, для которых₂(y)0, уравнение (2.1) равносильно уравнению:

.

(2.3)

В этом уравнении переменная yприсутствует только в левой части, а переменнаяx– в правой части. В дифференциалах уравнение (2.3) имеет вид:

.

(2.3а)

Каждая часть этого уравнения представляет собой произведение некоторого выражения, зависящего от одной переменной на дифференциал этой переменной. Его называют уравнением с разделёнными переменными.

Интегрируя почленно, получаем общее решение уравнения (2.1):

, или, гдеС = С₂ –С₁–постоянная.

Итак, для нахождения решения дифференциального уравнения с разделяющимися переменными следует: 1)разделить переменные; 2) интегрируя уравнение с разделёнными переменными, найти общее решение данного уравнения; 3) выяснить, имеет ли уравнение решения, не получающиеся из общего интеграла;

4) найти частное решение, удовлетворяющее начальным условиям (если это требуется).

Пример 1.Найти все решения дифференциального уравнения y' = xy².

• Очевидно, что y = 0 является решением данного уравнения.

Пусть теперь y 0. Тогдаи, следовательно,

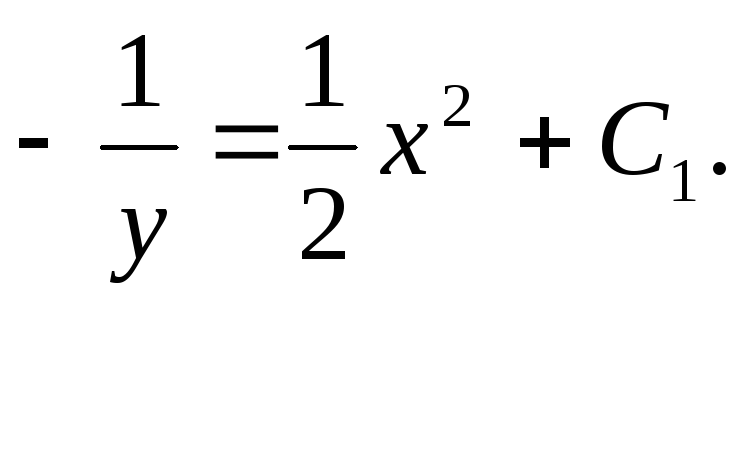
Таким образом, общее решение данного уравнения имеет вид , где.Заметим, что решение y= 0 не получается из общего решения ни при каком значении постояннойC.

Пример 2. Найти частное решение уравнения y' =2 + y , если y(0) = 3.

Δ Заменив y' на , а затем, умножив все члены наdx, получим

dy = 2dx+ ydx, т.е. dy = (2+y)dx.

Разделим обе части равенства на (2+y) и проинтегрируем:

;;ln(2+y) =x + ln|C|.

Выразим xчерез логарифм :x = lne^x. Тогда получим

ln(2 + y ) = lne^x + ln|C| .

Потенцируя, находим: 2 + y = C e^x,y = C e^x - 2.

Это общее решение данного уравнения. Подставим в общее решение x=0,y=3 и определимC: 3=C e⁰ - 2; 3 =C - 2;C = 5. Итак,y= 5e^x - 2.

Пример 3. Найти общее решение уравнения (x²y² -x²y)dy -xy²dx = 0,x0.

Δ Разделим переменные. Для этого преобразуем данное уравнение следующим образом:x²y(y-1)dy =xy²dx, или,

полагая y0. Проинтегрируем обе части последнего равенства:

,

откуда y-ln|y|=ln|x|+C_1.

Для удобства потенцирования представим yв видеy = ln e^y и постоянную интегрированияC₁в видеC₁= -ln|C|,C0. Имеем

lne^y-ln|y| =ln|x|-ln|C| .

Потенцируя, получим

, илиС e^y=xy,C0.

В процессе решения мы предполагаем y0. Однако легко убедиться проверкой, чтоy=0 – решение данного уравнения. Следовательно, сняв ограничениеС0, получим, что

Ce^y=xy

– общее решение данного уравнения. Решение y=0 получается отсюда как частное решение приC=0.

Отметим в заключение, что ряд задач на составление дифференциальных уравнений приводит к уравнению вида

,

(2.4)

где k − постоянная величина. Его смысл состоит в том, что скорость изменения функции пропорциональна самой функции.

Разделяя переменные и интегрируя, находим последовательно:

y=Ce^kx.

Общее решение раскрывает смысл названия уравнения (2.4). Его называют уравнением показательного роста.