
713
.pdf
Рис. 2.3. Зависимость угла 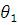 от времени tпри поворотах
от времени tпри поворотах
Каждая стадия движения характеризуется своим параметром. Настадии прямолинейного движения - это путь t: на переходной –
t: на переходной –
угол ; на круговой - угол
; на круговой - угол  (
( - радиус окружности, описываемой точкой
- радиус окружности, описываемой точкой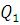 ). Для определения программы произвольного маневра необходимо задать n- количество угловых точек (т.е. таких, в которых осуществляется стыковка режимов движения) функции
). Для определения программы произвольного маневра необходимо задать n- количество угловых точек (т.е. таких, в которых осуществляется стыковка режимов движения) функции , включая момент начала движения, последовательность значений индексов
, включая момент начала движения, последовательность значений индексов  и значения управляющих параметров
и значения управляющих параметров  в точках
в точках
где
 ,
,
.
2.5. Аналитический расчет уравнений кинематики многозвенного автопоезда
В этом разделе рассматриваются случаи общего аналитического решения уравнения (2.7) и некоторых его частных случаев. Преобразуем уравнение (2.7) с помощью подстановки к виду
к виду
 (2.16)
(2.16)
Полученное уравнение представляет собой дифференциальное уравнение типа Риккати. Решение уравнения (2.16) в квадратурах можно получить, например, используя метод квазилинеаризации [22]
58
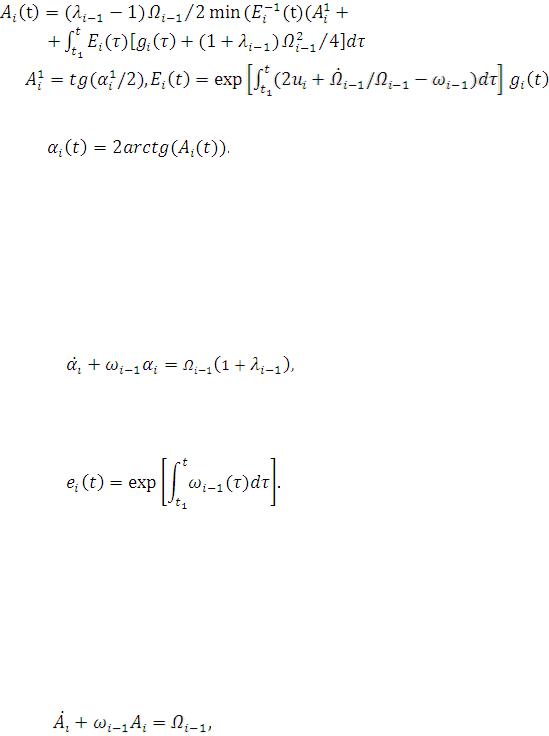
)), |
|
(2.17) |
где |
, |
- |
произвольная непрерывная на временном интервале T функция.Откуда
(2.18)
Однако анализ выражения (2.17) затруднен наличием операции взятия минимума. Поэтому решение уравнения (2.16) в общем случае целесообразно проводить численно с применением вычислительной техники.
Рассмотрим аналитическое решение уравнений (2.7), (2.16) в следующих важных частных случаях.
1. Малость углов  . В этом случае уравнение (2.7) сводится к линейному уравнению
. В этом случае уравнение (2.7) сводится к линейному уравнению
решением которого является
 .(2.19)
.(2.19)
Здесь и далее
2. Малость абсолютных скоростей поворота  При этом допущении уравнение (2.16) упрощается. Его решением будет
При этом допущении уравнение (2.16) упрощается. Его решением будет
 ,
,
следовательно,
 (2.20)
(2.20)
3. Равенство выноса точки сцепки (i - 1)-го звена базеi того ЭКЗ( ).
).
При этом уравнение (2.16) приобретает более простой вид
решением которого является
 [
[
 . (2.21)
. (2.21)
4. Постоянство радиуса кривизны основной траектории i-1 -го ЭКЗ .
.
59

= |
(2.22) |
Из уравнения (2.16), записанного в виде
с учетом (2.22) получим
(2.23)
 ,
, (2.24)
(2.24)
откуда определяются  , следовательно, и
, следовательно, и 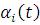 .
.
5. Малость отношения величины угловой скорости складывания i- гоЭКЗ к скорости движения (i -1) -го ЭКЗ 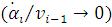 .
.
(2.25)
,
При  решение не существует.
решение не существует.
Для дальнейшего анализа уравнения (2.7) преобразуем его, применив операцию суммирования, к виду
 (2.26)
(2.26)
где
Далее, с учетом условий (2.1), (2.6) уравнение (2.26) можно переписать в следующей форме
(2.27)
где
(2.28)
Равенства (2.27)с условиями(2.28) представляют достаточно общую систему итерационных дифференциальных уравнений относительно
60

углов , обобщающих ряд имеющихся в публикациях по кинематике
, обобщающих ряд имеющихся в публикациях по кинематике
автопоезда уравнений ([21, 36, 45, 51, 55, 56, 60, 68]и др.).
Например, при N=2 из (2.27) можно получить уравнение, совпадающее с точностью до обозначений с уравнением (21) из [51]
(2.29)
Полученное уравнение (2.27), как и его частный случай (2.29), будучи нелинейным, в общем случае не поддается интегрированию в замкнутой форме и решение его, так же как и уравнения (2.29), возможно лишь с применением вычислительной техники. Однако при некоторых упрощающих предположениях уравнение (2.27) полностью интегрируется.
Полагая углы малыми и пренебрегая малыми величинами порядка
всоотношениях (2.4), (2.5), получим следующие равенства
сучетом которых после преобразования (2.27) получим
(2.30)
Здесь ,
,  ;
; . Решениеуравнения (2.30)
. Решениеуравнения (2.30)
не встречает принципиальных трудностей. Последовательно проводя интегрирование уравнения (2.30)дляi = 2,3,4 и т.д. можно определить искомые углы  для любого заданного N .
для любого заданного N .
Если определены решения ,…,
,…,  , тоструктура общего решенияi -того уравнения системы (2.30) такова
, тоструктура общего решенияi -того уравнения системы (2.30) такова
|
, |
(2.31) |
где |
- решение соответствующего однородного уравнения, |
- |
частное решение неоднородного уравнения, развернутые выражения которых несложно получить из вида системы (2.30).
Проведем аналитическое решение систем (2.30) в случае, когда
автопоезд состоит |
из кинематически |
одинаковых |
прицепных |
|
звеньев |
|
Система |
(2.30) при этом |
принимает |
более простой вид |
|
|
|
|
|
|
|
|
(2.32) |
где |
+λ, i = |
. |
|
|
61
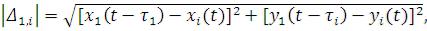
Значения углов  , определяемые из такой системы, для всех стадий
, определяемые из такой системы, для всех стадий
криволинейного движения автопоезда задаются формулами, приведенными в табл. 2.1.
Аналитические расчетные формулы (2.17), (2.19),(2.20),(2.21), (2.23),(2.24),(2.25) и формулы табл.2.1 позволяют оценивать влияния геометрических параметров, эксплуатационных режимов движения, скорости движения и числа звеньев автопоезда на величины углов 
(соответственно углов складывания  ).Следовательно,полученные
).Следовательно,полученные
соотношения позволяют определятьположение произвольного звена автопоезда какотносительно неподвижнойплоскости дороги, так и по отношению к направляющему звену, или относительно других звеньев автопоезда.
2.6. Определение характеристик маневренности автопоезда
При исследовании ряда вопросов маневренности и вписываемости подвижного состава большое практическое значение имеет решение задачи определения по заданным параметрам автопоезда и при заданном режиме движения траекторий любых точек автопоезда и ширины проезда, в которую сможет вписаться подвижной состав при совершении определенного маневра.
Знание текущих значений углов складывания, курсовых углов и значений координат точек, задающих основные траектории звеньев автопоезда, позволяет полностью определить основные характеристики маневренности автопоезда. К ним относят величину сдвига основной траекторииi-того прицепного звена от основной траектории автомобилятягача и параметры габаритной полосы движения автопоезда.
Сдвиг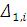 траектории i-того звена от основной траектории тягача
траектории i-того звена от основной траектории тягача
определим как расстояние между точками этих траекторий, замеренное в момент времени tпо нормали к основной траектории автомобиля-тягача, проходящей через точку Q
(2.33)
где значение  определяется из соотношения
определяется из соотношения
62

(2.34)
вытекающего из условия пересечения основной траектории автомобиля - тягача собственной нормалью, проходящей через точку (рис. 2.4).
(рис. 2.4).
Габаритная полоса движения автопоезда представляет собой фигуру, ограниченную левой и правой по ходу габаритными кривыми. Последние являются проекциями на плоскость  траекторий самых удаленных в данный момент времени левой и правой точек автопоезда от основной траектории направляющего звена. Габаритные кривые представим таким образом
траекторий самых удаленных в данный момент времени левой и правой точек автопоезда от основной траектории направляющего звена. Габаритные кривые представим таким образом
(2.35)
63
64

y
. 
.
.
.
.
.

0 . |
. |
. |
. |
x |
|
Рис. 2.4. Схема расчета сдвига траекторий 
65

Стадия
№криволинейного движения
1
2
,
3
*) Здесь
Таблица 2.1.
Формула 
66

Здесь индекс k обозначает принадлежность координат правой (k = п) или левой (k = л) габаритной кривой,  - координаты габаритных
- координаты габаритных
кривых ведущего звена, определяемые через |
илинейные |
||
габаритные размеры, |
, определяется аналогично |
: |
|
|
, |
(2.36) |
|
где отыскивается из соотношения: |
|
|
|
|
|
|
(2.37) |
- координаты габаритных кривых ведущего |
звена |
и |
|
ведомых звеньев |
, определяемые через |
|
и |
габаритные размеры этих звеньев. Таким образом, габаритную полосу движения (ГПД) автопоезда при заданных его геометрических параметрах (базе автомобиля-тягача и прицепных звеньев, продольных и поперечных габаритах и др.) формируют основная траектория автомобиля-тягача и величины сдвигов основных траекторий прицепных звеньев от
основных траекторий прицепных звеньев от
основной траектории автомобиля–тягача.
Эти главные элементы ГПД, в свою очередь, зависят от структуры автомобильного поезда и стадии его движения.
Расчет отмеченных характеристик, определяющих маневренные свойства многозвенного автопоезда, в общем случае движения целесообразно проводить с применением вычислительной техники.
2.7. Исследование частных случаев движения автопоезда
Для стадий прямолинейного, переходного и кругового движенияавтопоезда полученные выше формулы примут более простой вид. Исследуем эти частные случаи движения автопоезда.
1. |
П |
рямолинейное движение ( ).
).
В этом случае имеют место следующие соотношения
(2.38)
(2.39)
,
,(2.40)
(2.41)
67
