156

Содержание

Введение…………………………………………………………………….4

1.Матрицы………………………………………………………………….5

1.1.Основные понятия…………………………………………..5

1.2.Действия над матрицами……………………………………8

2.Определители…………………………………………………………...12

2.1.Вычисление определителей квадратных матриц второго и третьего порядков……………………………………..………..12

2.2.Определители более высоких порядков………………….19

3.Невырожденные матрицы……………………………………………..21

3.1.Определение………………………………………………..21

3.2.Способы нахождения обратной матрицы………………..22

4.Системы линейных уравнений………………………………………...25

4.1.Основные понятия…………………………………………25

4.2.Решение систем линейных уравнений методом Гаусса…28

4.3.Решение систем линейных уравнений по правилу Крамера………………………………………………………….30

4.4.Решение систем линейных уравнений матричным методом

(с помощью обратной матрицы)……………………………….32

5.Решение матричных уравнений……………………………………….34

6.Ранг матрицы…………………………………………………………...35

7.Исследование систем линейных уравнений………………………….38

8.Общее решение однородной системы линейных уравнений………..42

Задания по вариантам…………………………………………………….46

Заключение………………………………………………………………..79

Литература………………………………………………………………...81

3

Введение

Дисциплина «Линейная алгебра» относится к циклу общенаучных учебных дисциплин. Основная часть теоретического материала,

перечисленного в программе, излагается на лекциях. Главной задачей практических занятий является формирование и развитие умений и навыков,

необходимых для практического применения математического аппарата.

Данное пособие рассматривает основные темы линейной алгебры:

матрицы, определители и системы линейных уравнений. В первом разделе дается определение матрицы, рассматриваются основные виды матриц и действиям с ними. Каждое действие проиллюстрировано примером. Второй раздел посвящен различным способам вычисления определителей квадратных матриц. Рассматриваются такие методы, как правило треугольника, правило Саррюса, разложение по строке или столбцу, а также приведение определителя к треугольному виду. Третий раздел посвящен способам нахождения обратных матриц. Четвертый изучает способы решения систем линейных уравнений. Далее рассматривается решение матричных уравнений, дается определение ранга матрицы. Разобран вопрос совместности системы линейных уравнений. Для этого приводится теорема Кронекера - Капелли, с помощью которой исследуются системы линейных уравнений.

Пособие содержит 12 заданий, каждое из которых рассчитано на 30

типовых вариантов. Пособие может быть использовано при подготовке студентами-заочниками всех направлений.

4

1.Матрицы.

1.1.Основные понятия

Матрицей называется прямоугольная таблица чисел, содержащая m

строк одинаковой длины (или n столбцов одинаковой длины). Матрицы обозначаются прописными (заглавными) буквами латинского алфавита,

например A , B , C … Матрица записывается в виде

Матрицу A называют матрицей размера m × n и пишут Am×n . Числа aij

Матрица, у которой число строк равно числу столбцов, называется

квадратной. Квадратную матрицу размера п× п называют матрицей n -го

порядка.

Элементы, стоящие на диагонали, идущей из левого верхнего угла в правый нижний, образуют главную диагональ. Вторая диагональ

называется побочной.

5

Квадратная матрица, у которой все элементы, кроме элементов главной

диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой E .

Квадратная матрица называется треугольной, если все элементы,

расположенные по одну сторону от главной диагонали, равны нулю.

Различают верхнюю треугольную и нижнюю треугольную матрицы.

6

Матрица, содержащая один столбец или одну строку, называется

вектором (или вектор-столбец, или вектор-строка соответственно). Их вид:

Элементарными преобразованиями матриц являются:

•перестановка местами двух строк матрицы;

•вычеркивание (удаление) нулевой строки матрицы;

•умножение всех элементов строки матрицы на число, отличное

от нуля;

•прибавление ко всем элементам строки матрицы соответствующих элементов строки, умноженных на одно и то же число.

Те же операции, применяемые для столбцов, также называются

элементарными преобразованиями.

7

Теорема 1. Любую ненулевую матрицу можно путем элементарных преобразований свести к эквивалентной ей ступенчатой матрице.

Две матрицы A и B называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований.

Записывается A ~ B .

1.2.Действия над матрицами

1)Сложение матриц. Складывать можно только матрицы одинакового размера, при этом получается матрица той же размерности, что и исходные.

Свойства сложения:

1.A + B = B + A (коммуникативный закон).

2.( A + B) + C = A + (B + C) (ассоциативный закон).

3.Если O – нулевая матрица, то A + O = O + A = A .

2) Умножение на число. Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число.

8

Свойства умножения матрицы на число:

1.α × ( А+ В) = αА+ αВ ;

2.(α + β ) × А = αА+ βА;

3.α × (βА) = (αβ ) × А, где A , B , C — матрицы, α и β — числа.

Назовем разностью матриц A и B матрицу C , для которой C + B = A ,

т.е. C = A + (-1)B .

3) Умножение матрицы на матрицу. Операция умножения двух

матриц возможна, когда матрицы согласованны.

Матрицы A и B (порядок следования важен!) называются

соответствующие элементы j -го столбца матрицы B

cij = ai1b1 j + ai 2b2 j + K + aipbpj .

9

Решение

матрицы A и B квадратные одного размера, то произведения AB и BA

всегда существуют.

Умножение матриц обладает следующими свойствами:

1.А× (В×С) = ( А× В) ×С;

2.А× (В + С) = АВ + АС;

3.( А+ В) × С = АС + ВС ;

10

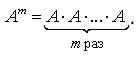
4.α ( АВ) = (αА)В , если, конечно, написанные суммы и произведения матриц имеют смысл.

5.При умножении на единичную матрицу АE = A и EA = A , т.е. при умножении матриц, единичная матрица играет роль единицы.

Решение.

4) Возведение в степень. Целой положительной степенью Am ( m > 1)

квадратной матрицы A называется произведение m матриц, равных A , т.е.

5) Транспонирование. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей

транспонированной к данной. Обозначается AT .

Транспонированная матрица обладает следующим свойством:

1. (AT )T = A ;

11