156

Матрица А−1 называется обратной по отношению к матрице A , если выполняется условие

А× А−1 = А−1 × А = Е ,

где E — единичная матрица того же порядка, что и матрица A . Матрица А−1

имеет те же размеры, что и матрица A .

Теорема 3. Всякая невырожденная матрица имеет обратную, которая вычисляется следующим образом

A−1 = 1 × (A* )T ,

A

где A - определитель матрицы, А* — союзная матрица.

Свойства обратной матрицы:

1. A−1 = 1 ;

A

2.( A × B)−1 = B −1 × A−1 ;

3.(A−1 )T = ( AT )−1 .

3.2.Способы нахождения обратной матрицы

1)«Классический» метод (с помощью алгебраических дополнений);

2)Метод Гаусса (с помощью элементарных преобразований).

22

Классический метод

(с помощью алгебраических дополнений)

1)Вычисление определителя матрицы A ;

2)Нахождение алгебраических дополнений Aij ;

3)Построение союзной матрицы А* ;

4)Нахождение обратной матрицы;

5) Проверка А× А−1 = А−1 × А = Е .

Решение.

23

Метод Гаусса

(с помощью элементарных преобразований)

1)Составление матрицы A E (к матрице A справой стороны приписывается единичная матрица E той же размерности, что и матрица A ).

2)С помощью элементарных преобразований над строками матрицы A E приводят ее к виду E A−1 .

3)Справа будет получена обратная матрица.

Решение.

24

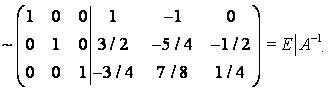
4.Системы линейных уравнений

4.1.Основные понятия

Линейными операциями над какими-либо объектами называются их

сложение и умножение на число.

Линейной комбинацией переменных называется результат применения к ним линейных операций, т. е.

α1x1 + α2 x2 + K + αn xn ,

где αi числа, xi − переменные.

Линейным уравнением называется уравнение вида

a1x1 + a2 x2 + K + an xn = b ,

где ai и b – числа, xi – неизвестные.

Линейное уравнение называется однородным, если b = 0 . В противном случае уравнение называется неоднородным.

Системой линейных уравнений (линейной системой) называется

система вида

Система уравнений называется совместной, если она имеет, хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим

решением.

Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.

Две системы называются эквивалентными (равносильными), если они имеют одно и то же множество решений. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой,

и наоборот.

Эквивалентные системы получаются при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.

Элементарными преобразованиями системы уравнений называют

следующие преобразования:

•перестановка любых двух уравнений;

•умножение обеих частей любого уравнения на любое число, отличное от нуля;

•прибавление к обеим частям одного из уравнений соответствующих частей другого, умноженных на любое число.

Система линейных уравнений называется однородной, если все

свободные члены равны нулю:

27

является решением системы. Это решение называется нулевым или

тривиальным.

4.2.Решение систем линейных уравнений методом Гаусса

Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных.

Пусть дана система уравнений

Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе выписывается расширенная матрица, которая приводится к ступенчатому виду (в частности, треугольному, это матрица, у которой под главной диагональю все нули).

На втором этапе производится переход от расширенной матрице обратно к системе, затем идет последовательное определение неизвестных переменных из последней строки системы, поднимаясь по ступени вверх.

x + 3y − z = 4

Пример 22. Решить систему методом Гаусса: 2x − y − 5z = −15

5x + y + 4z =19

28

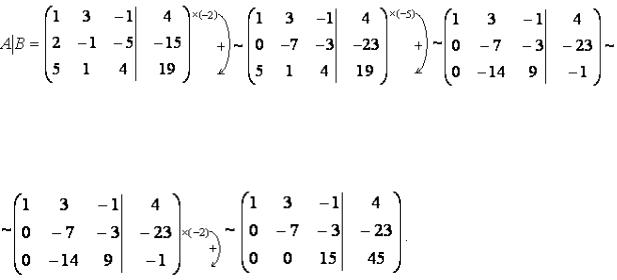
Решение.

Записываем расширенную матрицу. Затем первое уравнение умножим на -2 и прибавим ко второму, и первое умножим на -5 и прибавим к третьему.

Получим

Теперь прибавим ко второму уравнению, умноженному на -2, третье уравнение. Получим

По ступенчатому виду расширенной матрицы выписываем систему

Решение.

В результате элементарных преобразований над расширенной матрицей системы получим

29

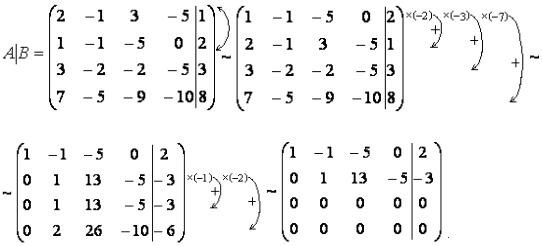
По ступенчатому виду расширенной матрицы выписываем систему

получаем общее решение системы линейных уравнений. Если положить,

например, x3 = 0 , x4 = 0 то найдем одно из частных решений этой системы

(−1;−3;0;0) .

4.3.Решение систем линейных по правилу Крамера

Рассмотрим систему трех уравнений первой степени с тремя

при неизвестных данной системы, называется главным определителем этой

системы.

30

Рассмотрим следующие возможные случаи.

1. D ¹ 0 Тогда решение системы находим как

при этом полученные формулы называются формулами Крамера.

Решение.

31