156

2. (λA)T = λAT ;

3 ( A + B)T = AT + BT ; 4. ( A × B)T = AT × BT .

2.Определители

2.1.Вычисление определителей квадратных матриц второго и

третьего порядков

Любой квадратной матрице A порядка n можно поставить в соответствие по определенному закону некоторое число, называемое определителем, или детерминантом, n -го порядка этой матрицы.

Обозначается определитель det A (или A , или ), и вычисляется следующим образом:

Вычисление определителя 2-го порядка можно проиллюстрировать схемой

при этом из произведения элементов, стоящих на главной диагонали матрицы вычитается произведение элементов, стоящих на побочной диагонали.

12

Решение.

A= 2 -3 = 2 × 6 - 7 × (-3) =12 - (-21) =12 + 21 = 33. 7 6

3.Определителем третьего порядка. Для вычисления определителя третьего порядка, применяют две вычислительные схемы, позволяющие вычислять определители третьего порядка без особых хлопот. Эти схемы известны, как правило треугольника (или правило звездочки) и правило

Саррюса.

1) Правило треугольника (или правило звездочки). При вычислении определителя 3-го порядка удобно пользоваться правилом треугольника,

которое символически можно записать так

По правилу треугольника сначала перемножаются и складываются элементы, соединенные на схеме линиями

,

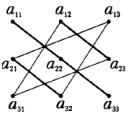т. е. получаем сумму произведений: a11a22a33 + a12a23a31 + a21a32a13 .

Затем перемножаются и складываются элементы, соединенные на схеме линиями

13

,

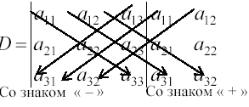
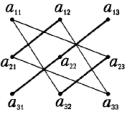т. е. получаем другую сумму произведений a31a22 a31 + a21a12 a33 + a32 a23 a11 .

И, наконец, чтобы вычислить определитель, из первой суммы вычитаем вторую, и окончательно получаем

=a11a22a33 + a12a23a31 + a21a32a13 − (a13a22a31 + a21a12a33 + a32a23a11) =

=a11a22a33 + a12a23a31 + a21a32a13 − a13a22a31 − a21a12a33 − a32a23a11 .

2)Правило Саррюса. По правилу Саррюса, к определителю справа дописывают два первых столбца, а затем считают сумму произведений элементов определителя в направлении главной диагонали, и из нее вычитают сумму произведений элементов в направлении побочной диагонали (см. схему).

Можно убедиться, что результат будет таким же, что и при вычислении определителя по правилу треугольника.

Решение.

а) по правилу треугольников:

14

б) по правилу Саррюса:

Определители обладают следующими свойствами.

Свойство 1 . Определитель не изменится, если его строки заменить столбцами и наоборот, т.е. при транспонировании.

Свойство 2. Общий множитель любой строки (столбца) можно

вынести за знак определителя.

Свойство 3. Определитель, имеющий нулевую строку (нулевой

столбец), равен нулю.

Свойство 4. Определитель, имеющий две равные строки (два

одинаковых столбца), равен нулю.

Свойство 5. Определитель с пропорциональными строками равен

нулю.

Свойство 6. При перестановке двух строк или двух столбцов определитель меняет его знак.

Свойство 7. Если элементы какого-либо столбца (строки)

представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

Например,

15

Свойство 8. Определитель не изменится, если к элементам одного столбца (строки) прибавить соответствующие элементы другого столбца

(строки), умноженные на любое число.

Например,

Кроме правила треугольника (или правила звездочки) и правила Саррюса есть еще два способа вычисления определителей матриц..

3) Разложение определителя по строке или столбцу.

Минором некоторого элемента aij определителя n -го порядка

называется определитель n − 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается M ij .

Решение.

Алгебраическим дополнением элемента aij определителя называется его минор, взятый со знаком «плюс», если сумма индексов i + j – четное

16

число, и со знаком «минус», если эта сумма нечетная. Обозначается

Aij = (-1)i+ j × M ij .

При этом полезно иметь в виду схему

+− +

−+ − ,

+− +

где знаки «+» или «−» чередуются, ими помечены места тех элементов, для которых алгебраические дополнения равны минорам или отличаются от них знаком.

Пример 15. В условиях предыдущего примера найти алгебраические

дополнения A2,1 и A2,2 .

Решение.

A2,1 = (−1)2+1 M 2,1 = −11, A2,2 = (−1)2+2 M 2,2 = −2 .

Теорема 2 (Лапласа). Определитель равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения.

n = ai1 Ai1 + ai 2 Ai 2 + ... + ain Ain

Данная формула называется разложением определителя по i строке.

Аналогичное утверждение имеет место и для разложения определителя по любому столбцу.

Решение.

17

4) Приведение определителя к треугольному виду. С помощью элементарных преобразований над строками определитель приводится к ступенчатому виду и тогда его значение равно произведению элементов,

стоящих на главной диагонали.

Для этого мы поменяем местами первый и третий столбцы определителя, что согласно свойствам определителей, приведет к тому, что он сменит знак на противоположный:

Первую строку умножим на 3 и прибавим к третьей строке

1 3 2

= − 0 − 13 − 3 =

0 11 12

18

Теперь поменяем местами 2 и 3 столбца, что приведет к смене знака

Прибавим ко второй строке, умноженной на 4, третью строку. Получим

Тогда значение определителя равно произведению элементов, стоящих на главной диагонали.

2.2.Определители более высоких порядков

Для квадратных матриц размерности n × n при n > 3 можно также

записать определитель n -го порядка

Свойства определителей 3-го порядка справедливы и для определителей n -го порядка.

На практике определители высоких порядков вычисляют с помощью разложения по строке или столбцу. Это позволяет понизить порядок вычисляемых определителей и, в конечном счете, свести задачу к

19

нахождению определителей 3-го порядка. Так, вычисляя определитель четвертого порядка путем разложения его по элементам строки или столбца,

придется вычислить 4 определителя третьего порядка.

Решение.

4-1 1

+3 × (18 + 8 +1 +12 - 3 + 4) - 4 × (6 + 20 - 3 - 36 -1 +10) =

=1× (-28) - 2 × 60 + 3 × 40 - 4 × (-4) = -28 -120 +120 + 16 = -12 .

Задача упрощается, если предварительно определитель можно преобразовать, используя его свойства, таким образом, чтобы в какой-либо строке или столбце все элементы, кроме одно, стали нулевыми. Тогда алгебраические дополнения этих элементов вычислять не нужно, т.к.

соответствующие слагаемые в разложении определителя равны нулю из-за умножения на нулевые элементы.

20

Решение. Первую строку умножим на (-5) и прибавим ко второй, затем первую строку умножим на 4 и прибавим к третьей строке, и на (-7) и

прибавим к четвертой, получим

=-1× (441 + 234 + 63 - 273 -189 -126) = -1×150 = -150 .

3.Невырожденные матрицы

3.1.Определение

Матрицей, союзной к матрице A , называется матрица, составленная из алгебраических дополнений

21