Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский Государственный аграрно-технологический университет им. Д.Н. Прянишникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2021_082

.pdf

Скачиваний:

Добавлен:

01.01.2024

Размер:

3.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

нием трех чисел

, где

- длина радиуса – вектора про-

екции точки

на плоскость

Oxy

- угол, образованный

этим радиусом вектором с осью Ox ,

- аппликата точки

Эти три числа

координатами точки

(r; ; z)

M .

называются цилиндрическими

Цилиндрические координаты точки (r; ; z) связаны с декартовыми координатами следующими соотношениями:

где

[0;2

]

x r cos
		,
y r sin
	z z

z R .

Вычислим якобиан преобразования:

	x	x	x
	r		z	cos	r sin
J (r; ; z)	y	y	y	sin	r cos
J (r; ; z)	r		z	sin	r cos
	r		z	0	0
	z	z	z	0	0
	z	z	z
	r		z

0 0 1

r cos	2

r sin	2

Формулы замены примут вид:

f (x; y; z)dV V


V

(r cos ;r sin ; z)rdrd dz

Таким образом, вычисление тройного интеграла приводится к интегрированию по r , по и по z аналогично тому, как это делается в декартовых координатах.

Замечание. К цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.

Пример 17. Вычислить 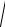x2 y2 dxdydz , если область

ограничена поверхностями	x	2	y	2	4	,	z 1,	z 2 x	2	y	2	.

Решение. Строим область интегрирования V

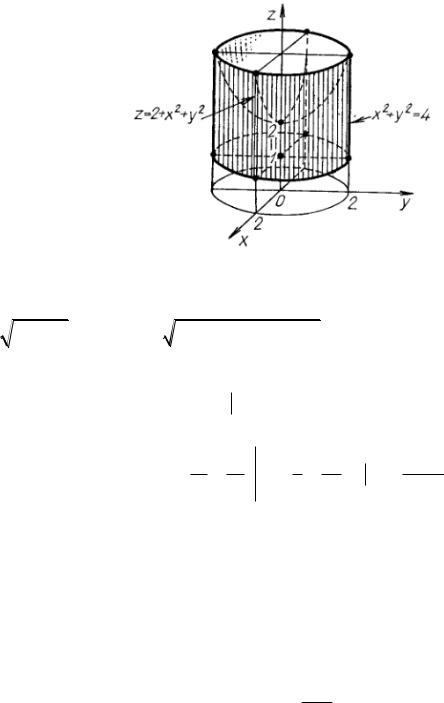
Рисунок 28 - Построение области

	x	2	y	2	dxdydz	r	2	cos	2	r	2	sin	2	rdrd dz
		2		2			2		2		2		2
V					V

2	2				2 r		2	2	2									2		2
2	2				2 r			2	2					2 r		2		2		2
d r		2						dz d r		2						2		d r			2	(1 r		2	)dr
		2	dr							2		dr z									2			2
			dr									dr z		1
0	0				1			0	0									0		0
2	2							2	r		3				5		2									272
2	2							2			3		r		5				8	32			2
d (r			2	r		4							r						8	32			2
d (r				r				)dr d															0
0	0							0		3				5			0		3	5						15
																	0

Вычисление тройного интеграла в сферических координатах

Сферические координаты точки M (x; y; z) пространства

Oxyz называется тройка чисел r , , , где r			- длина радиуса
– вектора проекции точки M , - угол, образованный проек-
			и осью Ox , -
цией радиуса – вектора OМ на плоскость Oxy

угол отклонения радиуса – вектора OМ

от оси Oz .

Сферические координаты

(r; ; ) , связаны с декартовы-

ми координатами следующими соотношениями:

x r cos sin

y r sin sin ,
	z r cos
	z r cos
где r 0 , 0 2 , 0 ,	z R .
	42

В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам. Для этого нужно воспользоваться формулой замены переменных в тройном интеграле.

Вычислим якобиан преобразования:

	x	x	x
	r			cos sin	r sin sin	r cos cos
	y	y	y
J (r; ; )				sin sin	r cos sin	r sin cos
	r
				cos	0	r sin
	z	z	z

	r

r2 cos2 sin3 r2 sin2 cos2 sin r cos2 cos2 sin r2 sin2 sin3

r2 sin3 (cos2 sin2 ) r2 cos2 sin (sin2 cos2 )

r2 sin3 r2 cos2 sin r2 sin (sin2 cos2 ) r2 sin .

Формулы замены примут вид:

f (x; y; z)dV V


V

f (r cos sin ;r sin sin ;r cos )r	2	sin drd d

Замечание. Переходить к сферическим координатам удобно, когда область интегрирования V есть шар (уравне-

ние его границы

в сферических координатах

имеет вид r R )

или его часть,

а также, если подынтеграль-

ная функция имеет вид

f (x

) ).

Пример 18. Вычислить

x	2	y	2	z	2	1.
	2		2		2

			dxdydz
								3
V	1	(x	2	y	2	z	2	)
								2

, где

- шар,

Решение. Вычислим интеграл путем перехода к сферическим координатам:

x r cos sin

y r sin sin .
	z r cos

Граница области

- сфера, и ее уравнение имеет вид

r 1. Подынтегральная имеет вид

функция после замены переменных

			1																												1
											3
											3
(x	2	y		2	z				2	)	2				1 ((r cos sin )											2		(r sin sin
(x		y			z					)					1 ((r cos sin )													(r sin sin

																		1
																																	3
(r		2	cos			2		sin				2	r				2	sin			2	sin		2	r				2	cos		2	)
																																	2
																1
																														3
																														3
(r		2	sin		2							2		sin					2	) r			2	cos			2	)				1 (r
(r			sin				(cos							sin						) r				cos				)		2		1 (r
																														2
								1														1				.
																		3							3	.
																		3							3
(r		2	(sin			2		cos							2	))		2			1 r		2
																		2							2

				3
				3
)	2	(r cos )	2	)
				2

			1
							3
							3
2	sin	2	r	2	cos	2	)
							2

Новые переменные изменяются в следующих пределах:

r [0;1],

0 2

, 0 , z R .

Таким образом, согласно полученной формуле

				dxdydz															1					2												2	1				r	2	dr
				dxdydz								3							1			3	r		sin drd d sin d d																r		dr
												3										3	r		sin drd d sin d d																				3
V	1 (x			2	y	2	z		2		)				V		1 r				2										0					0	0		1			r		2
												2										2																							2
																									1		d (r	3	)
					2				2												2							3						2				3
					2		1	r	2	dr											2		1		3					1				2		1	d (r	3		1)
sin d d								r		dr			sin d d																	1	sin d d						d (r			1)

								1 r				3													1 r			3		3							1 r				3
	0				0		0	1 r							0						0		0		1 r					3	0			0		0	1 r
	0				0		0								0						0		0								0			0		0
	1				2										3	1		1							2								1								2
	1	sin d d ln 1 r														1		1		sin d d (ln 2											ln1)		1		ln 2 sin d							d
		sin d d ln 1 r																		sin d d (ln 2											ln1)				ln 2 sin d							d

	3	0			0											0		3		0						0							3			0						0
		0			0															0						0										0						0
	1								2					2													2									4	ln 2 .
	1	ln 2		sin d					2					2		ln 2				sin d							2	ln 2 ( cos )								4
	3								0						3												3					0				3

			0																0
			0																0

3.2.4 Применение тройного интеграла

1. Вычисление массы тела

при заданной объемной

плотности

(x;

Вычисление массы производится по формуле

m (x; y; z)dxdydz ,

где

(x; y; z)

– объемная плотность распределения массы в

точке

M (x; y; z) .

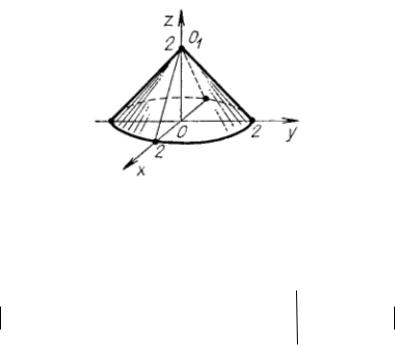
Пример 19. Вычислить массу тела, ограниченного по-

верхностью конуса	(z 2)	2	x	2	y	2	и плоскостью z 0	, если

плотность тела (x; y; z) z .
Решение. Строим область интегрирования	V . Вершина


конуса находится в точке	О1 (0;0;2) , и в сечении конуса плос-
костью z 0 получается окружность x		2	y	2	4 .
костью z 0 получается окружность x			y		4 .

Рисунок

m (x; y; z)dxdydz
	V		V
2	2	2	2
d rdr z 02 r d r(2
0	0	0	0

29 - Построение области V

	2		2		2 r
zrdrd dz d rdr dz
	0		0		0
2		2		r3 2				8	2	8
r)dr d r							4		0		.
r)dr d r							4		0		.
0				3		0		3		3

2. Вычисление объемов тел.

Объем области V выражается формулой

V dxdydz – в декартовых координатах, V

V rdrd dz

– в цилиндрических координатах,

V r	2	sin drd d
	2
V

– в сферических координатах,

Пример 20. Вычислить объем тела, ограниченного поверхностями z 1, z 5 x2 y2

Решение. Строим область интегрирования V

x 4.

Рисунок 30 - Построение области V

			2	2		5 r	2		2		2
			2	2		5 r			2		2	5 r	2
V rdrd dz d rdr							dz d rdr z						2

												1
	V		0	0		1			0		0
2	2			2	2					2					4	2
2	2			2	2					2				r	4		2
d r(4 r		2						3				2
		2	)dr d (4r				r	3	)dr	d 2r		2				(8 4)
			)dr d (4r				r		)dr	d 2r				4		(8 4)	0
0	0			0	0					0				4		0
																0

3. Вычисление статистических моментов тела и координат его центра масс тела

Моменты плоскостей Oxy

xy ,

Oxz

xz , S yz тела относительно координатных Oyz вычисляются по формулам:

Sxy z (x; y; z)dxdydz ,

Sxz y (x; y; z)dxdydz V

S yz x (x; y; z)dxdydz V

Координаты центра масс тела

находятся по формулам

Пример 21.

родного тела	V ,
x 4.

xc	S yz	, yc	Sxz	, zc	Sxy	.
	m		m
					m

Вычислить координаты центра масс одноограниченного поверхностями x y2 z2 и

Решение. Решение. Строим тело, ограниченное данными поверхностями. Область V ограничена поверхностью параболоида, отсеченного плоскостью

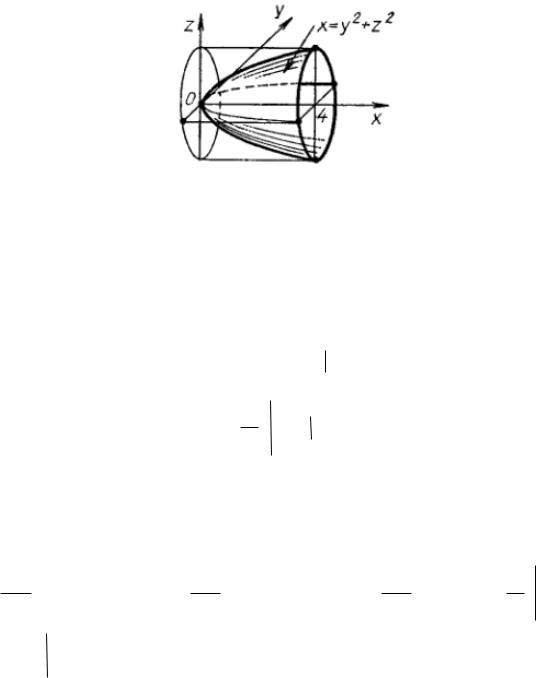
Рисунок 31 - Построение области

Его проекция на плоскость	Oyz	представляет собой
круг, ограниченный окружностью	y2 z2	4 . Вычислим мас-

су тела в цилиндрических координатах, считая, что его плотность 1:

		2	2
dxdydz d
V		0	0
2			2
d (4r r	3	)dr
d (4r r		)dr
0			0

4
rdr dx
r	2

		2
d 2r

	2		2
d rdr x
	0		0
		4	2
	r			2

	4			0

			0

r		2		2
r
4			d		r
	2		d		r
	2
		0		0
(8 4) 8

(4 r	2	)dr

Тогда

		1							1	2	2		4			1	2			2		x		2	4
										2	2		4				2			2				2	4
xc				xdxdydz						d rdr xdx								d rdr
xc		m		xdxdydz				8		d rdr xdx					8			d rdr
		m		V				8		0	0		r2		8			0		0			2		r2
				V						0	0		r2					0		0					r2					2
			2		2								2	2										2					5	2
	1		2		2						1		2	2							1			2				r	5
	1			d	r(16 r				)dr		1		d (16r			r			)dr		1					8r		r
				d	r(16 r		4		)dr				d (16r			r		5	)dr					d		8r	2
							4											5									2
	16			0	0						16		0	0							16			0				5		0
				0	0								0	0										0

	1			2		32				1				32		16
					24							2	24					.
	16				24							2	24					.
	16			0		5			16					5		5

Аналогично определяются	yc	и	zc , но так как тело – од-
нородное и симметричное относительно Ox , то y 0 и				z	c	0 .
			c		c

4. Вычисление моментов инерции тела

Момент инерции тела относительно координат вычисляется по формуле:

I0 (x2 y2 z 2 ) (x; y; z)dxdydz .

Моменты инерции тела относительно координатных плоскостей находятся по формулам

I I I

xy z V

xz y V

yz x V

(x; y; z)dxdydz

Моменты инерции относительно координатных осей по формулам

I x ( y	2	z	2	) (x; y; z)dxdydz
	2		2
V

(x2

(x2 V

z 2 ) (x; y; z)dxdydz ,

y	2	) (x; y; z)dxdydz .

Пример 22. Вычислить моменты инерции однородного шара радиуса R и весом P относительно центра и диаметра.

Решение.

постоянна

Так как объем шара V			4	R	3	, то его плотность
					3
			3
			3
3P		. Поместим шар в начало координат, то-
4g R	3	. Поместим шар в начало координат, то-
	3

гда			его			поверхность будет определяться
x	2	y	2	z	2	R	2	. Момент инерции относительно

удобно вычислить в сферических координатах:

уравнением центра шара

I0 (x				2	y	2	z			2	)dxdydz r				4					2					R	4	dr
I0 (x					y		z				)dxdydz r					sin drd d d sin d r											dr

			V											V						0	0				0
	2						r	5		R		R	5	2				R	5 2		R		5
	2							5					5	2					5 2				5	2
d sin d														d cos						d				2
d sin d							5					5		d cos			0	5		d		5		0
	0		0				5		0			5		0				5		0		5
	0		0						0					0						0
		2 R5			3 P	R2 .

			5		5 g
			5		5 g

Так как вследствие однородности и симметрии шара его моменты инерции относительно любого диаметра равны, вычислим момент инерции относительно диаметра, лежащего на оси Oz :

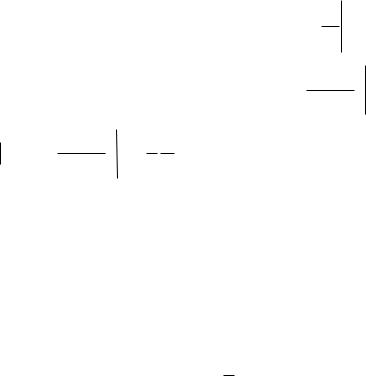
I z

(x				2	y			2	)dxdydz r								2	sin			2	r		2		sin drd d
				2				2									2				2			2
	V														V
	2									R					2														r	5	R
	2									R					2															5
d sin						3	d			r	4	dr d (1 cos													2		)sin d
						3					4														2
	0		0							0					0		0												5		0
	0		0							0					0		0														0
	R	5	2																R				5	2				cos3
	R		d (1 cos										2	)d cos					R									cos3
	5		d (1 cos											)d cos							5			d					3
	5		0			0															5			0					3			0
			0			0																		0								0
	R	5		2						cos3						2 P
		5
																		R	2	.
				0														R		.
	5			0							3					5 g
	5										3				0	5 g
															0

Задачи для самостоятельного решения

1. Вычислить объем тела, ограниченного поверхностями

z x

, z 1

. (Ответ: .)

2. Найти массу шара

2Rz , если плотность в

каждой точке шара обратно пропорциональна расстоянию от

нее до начала координат. (Ответ:	4	kR	2	.)

	3

3.	Найти координаты
радиуса	R , если плотность
			2R
центра шара. (Ответ:		0;0;
центра шара. (Ответ:		0;0;
			5

центра тяжести половины шара пропорциональна расстоянию от

4. Найти моменты цилиндра относительно

инерции однородного ( диаметра основания и оси.

const ) (Ответ:

		kHR	4
I		kHR
I	x	4
	x

kH	3	R	2		kHR	4
				, I y		.)
3					2

Вопросы для самоконтроля

1.Как вычисляется масса пластинки через тройной

интеграл?

2.Как вычисляется объем тела в декартовых коорди-

натах?

3.Как вычисляется объем тела в цилиндрических координатах?

4.Как вычисляется объем тела в сферических коор-

динатах?

5.Как найти координаты центра масс?

4 САМОСТОЯТЕЛЬНАЯ РАБОТА ПРИ ПОДГОТОВКЕ К ТЕКУЩЕМУ КОНРОЛЮ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ

4.1 Рекомендации при подготовке к текущему контролю и промежуточной аттестации

В ходе самостоятельной работы при подготовке к текущему контролю и промежуточной аттестации раздела «Двойные и тройные интегралы» дисциплины «Математика» обучающимся необходимо следующие:

-выполнить домашнюю контрольную работу;

-ответить на вопросы для экзамена;

-решить тест для подготовки к экзамену.

Контроль результатов работы обучающихся осуществляется в виде решения домашней контрольной работы. Для этого в методических рекомендациях даны задания по вариантам, для самостоятельной работы дома. Для их выполнения рекомендуется, использовать основные учебники и дополнительную литературу, а также материал, представленный в данных методических рекомендациях.

Если в процессе самостоятельной работы возникают затруднения, обучающемуся следует обратиться за консультацией на кафедру к преподавателю, ведущему занятия в соответствующей группе.

Основная форма контроля знаний по окончании изучения дисциплины – промежуточная аттестация, которая проходит в виде экзамена. Для подготовки к экзамену обучающемуся необходимо ответить и законспектировать ответы на все вопросы для подготовки к экзамену, представленный в данных методических рекомендация, а также решить тест.

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.01.20243.7 Mб02021_077.pdf
#
01.01.2024692.06 Кб02021_078.pdf
#
01.01.20243.03 Mб02021_079.pdf
#
01.01.20244.02 Mб02021_080.pdf
#
01.01.20241.76 Mб02021_081.pdf
#
01.01.20243.23 Mб02021_082.pdf
#
01.01.20241.23 Mб12021_083.pdf
#
01.01.20241.8 Mб02021_084.pdf
#
01.01.20241.3 Mб02021_085.pdf
#
01.01.20244.75 Mб02021_086.pdf
#
01.01.20244.82 Mб12021_087.pdf