Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский Государственный аграрно-технологический университет им. Д.Н. Прянишникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2021_082

.pdf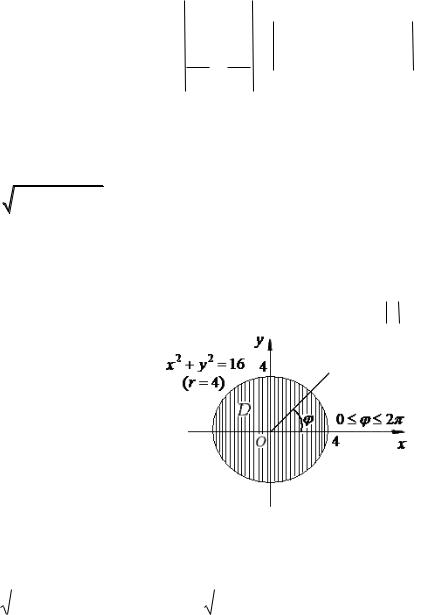

Скачиваний:

Добавлен:

01.01.2024

Размер:

3.23 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

D	в область	D		не выполняют, а, совместив декартову и по-

лярную системы координат, находят нужные пределы инте-

грирования по r и	(исследуя закон изменения		r и точки
(r; ) при ее отождествлении с точкой (x; y) ; области D ).
3. Для области,	ограниченной эллипсом	x2		y2	1, по-
		a2
				b2

лезно пользоваться обобщенными полярными координатами x a r cos , y b r sin .

Якобиан имеет вид:

	x	y
J (r, )	r	r	a cos
	r	r
	x	y	bsin
	x	y

	ar sin
	br cos
	br cos

abr

Тогда

	f (x; y)dxdy ab
D( x, y)		D(r, )

(ar cos ;br sin )rdrd

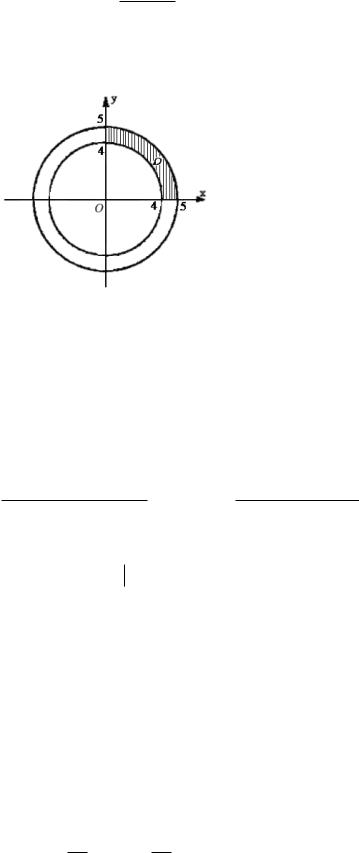
Пример

Вычислить

двойной

интеграл

	16 x	2
		2
D

y	2	dxdy

, если область

- круг

x	2	y	2

x r cos

Решение. Перейдем к полярным координатам

y r sin

Получим r

sin

или

r 4 .

cos

Рисунок 15 - Построение области D

		2	4
		2	4
	16 x2 y2 dxdy d			16 (r cos )2 (r sin )2	rdr
D	0		0

	2		4	16 r			(cos					sin											2				4	16 r										rdr
	d			16 r			(cos					sin							) rdr d									16 r										rdr
						2					2							2																		2
	0		0																				0				0
	1	2		4				2			2			1		2				4				2									2
	1	d			16 r				dr					1			d 16						r		d (16 r										)
		d			16 r				dr								d 16						r		d (16 r										)

	2	0		0										2			0			0
		0		0													0			0
			2		4																		2				16 r							2	3/ 2				4
			2		4																		2											2	3/ 2				4
		1	d 16 r 2							1/ 2 d (16 r 2 )												1	d
		2	d 16 r 2							1/ 2 d (16 r 2 )												2	d					3/ 2
		2	0		0																	2	0					3/ 2											0
			2												2											128													0
			2												2
		1	d 0 163/ 2										64		d						64		02							.
		3	d 0 163/ 2												d								02							.
		3	0									3			0					3							3
			0												0
						Задачи для самостоятельного решения
			1.		Вычислить двойной интеграл																														(x		2	y		2	)	3	dxdy , если
			1.		Вычислить двойной интеграл																														(x			y			)		dxdy , если
																														D
область					D -	круг радиуса														R		с центром в начале координат.
					2 R
					5
(Ответ:					5	.)
					5																							x2							y2 dxdy , если об-
			2. Вычислить двойной интеграл																									x2							y2 dxdy , если об-
																												D
ласть D ограничена окружностью																									x	2	y		2		4x . (Ответ: 24 .)
ласть D ограничена окружностью																									x		y				4x . (Ответ: 24 .)
			3. Вычислить двойной интеграл																											х		2		уdxdy , если область
			3. Вычислить двойной интеграл																											х				уdxdy , если область

ограничена	х	2	у

4. Вычислить

2	4	,	х	2
2				2

двойной

				D
у	2	16	,	х

интеграл

0 ,

		(
	D	(
	D

у 0 . (Ответ:							992		.)
у 0 . (Ответ:								15	.)
								15
	dxdy					, если		об-
x	2	y	2	)	2	, если		об-
	2		2		2

ласть

ограничена окружностями

x	2	y	2

x	2	y	2	8x
	2		2

прямыми

. (Ответ: 1283 .)

5.	Вычислить двойной интеграл	хуdxdy
		D
ограничена х2 у2 1, х2 у2 5 . (Ответ:			0 .)
6.	Вычислить двойной интеграл	sin	х2

,если область

у2 dxdy , если

область D - круг х2 у2 2 . (Ответ: 2 2 .)

Вопросы для самоконтроля

1.Зачем необходимо в двойном интеграле переходить к полярным координатам?

2.Как от декартовой системы координат перейти к полярной?

3.Как вычисляется Якобиан перехода?

4.Как сделать замену в двойном интеграле?

3.1.4 Применение двойного интеграла 1. Вычисление площади плоской области

			S dxdy – в декартовых координатах,
				D
				S rdrd – в полярных координатах.
				D
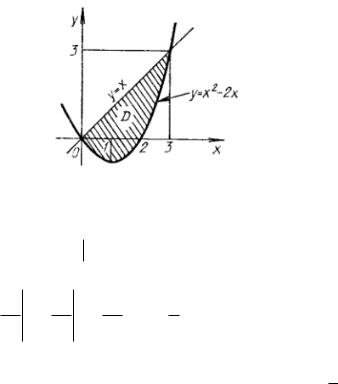
Пример 7. Вычислить площадь фигуры, ограниченной
кривыми y x			2	2x , y x .
кривыми y x				2x , y x .
Решение. Изобразим область D . Найдем точку пересе-
чения: x x	2	2x или x(x 3) 0 x 0 или x 3 .
чения: x x		2x или x(x 3) 0 x 0 или x 3 .

Рисунок 16 - Построение области

			3		x				3
S dxdy dx						dy dx
	D		0	2	2 x				0
	D		0	x	2 x				0
3		3				x	2	3		x	3
3		3					2				3
	xdx		x2dx 3

3						2				3
0		0				2		0		3
0		0

	x				3
y	x					(x
y	x	2	2 x			(x
		2

					0
3			27
			27	9
			2	9
0			2
0

			3
x		2	2x)dx (3x x	2	)dx
x			2x)dx (3x x		)dx
			0
9	.
2	.
2

Пример 8. Вычислить площадь фигуры, ограниченной кривыми x2 2x y2 0 , x2 4x y2 0 , y x , y x3 .

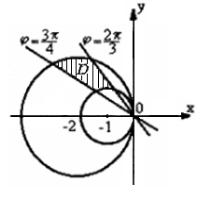
Решение. Преобразуем уравнения линий

(x		2	2x 1)	1 y	2	0	или (x 1)	2		y	2		1,

(x	2	4x 4) 4 y			2	0	или (x 2)		2	y		2	4

Изобразим фигуру на рисунке

Рисунок 17 - Построение области

При вычислении площади удобно перейти к полярным

x r cos	.
координатам	.
y r sin

Преобразуем условия:

1) Окружность	x
уравнение

2x y	2	0
	2

имеет полярное

(r cos )			2

r	2		2
		(cos

2r cos (r sin
sin	2	) 2r

)	2	0

cos ,

r	2	2r cos

или

2cos

2) Окружность уравнение

x	2	4x y	2	0
	2		2

имеет полярное


	(r cos )			2	4r cos (r sin )	2	0	,
	(r cos )				4r cos (r sin )		0	,
	r 2 (cos2 sin 2 ) 4r cos ,
	r	2	4r cos или r 4cos .
	r		4r cos или r 4cos .
3) Прямая	y x имеет полярное уравнение
	r sin r cos или sin cos ,
делим левую и правую часть на cos

	tg 1	или	3	.
			4

4) Прямая y x	3 имеет полярное уравнение
r sin	3r cos	или sin			3 cos ,
делим левую и правую часть на cos

или

		2
		3
		3

			3
		4		4cos
S dxdy d					rdr
D			2	2cos
		3
3	2			3	1
4	2			4	1
4				4
6 cos		d 6
2				2
3				3

3 3

3 d 3 cos2 d

2 2

3 3

			3							4cos			3
4						r	2			4cos		4		16cos	2	4cos	2
						r								16cos		4cos
d

					2							d		2		2
			2		2					2cos			2	2		2
3										2cos		3
3												3
											3
cos2									4
cos2
				d 3 (1 cos2 )d
2											2
									3
		3						3
4					3				4
3 d									cos2 d (2 )
3 d									cos2 d (2 )
		2			2 2
	3								3

	3		3			3		3	2
3			3	sin 2				3	2
3	4			sin 2		4	3
	2					2
	2		2			2		4	3
	3		2			3		4	3
	3					3
9 8					3			3		3
3						1

		12			2			2	4	2
		12			2			2	4	2

3 2


sin

3	3
	2

3	sin	4
	sin
2		3

2. Вычисление объемов тел

Объем цилиндрического тела находится по формуле

(x;

y)dxdy

где z f (x; y) - уравнение поверхности, ограничивающей тело сверху.

Если тело ограничено двумя поверхностями	z f1(x; y)	и
z f2 (x; y) , то его объем определяется по формуле:
V ( f2 (x; y) f1(x; y))dxdy .
D

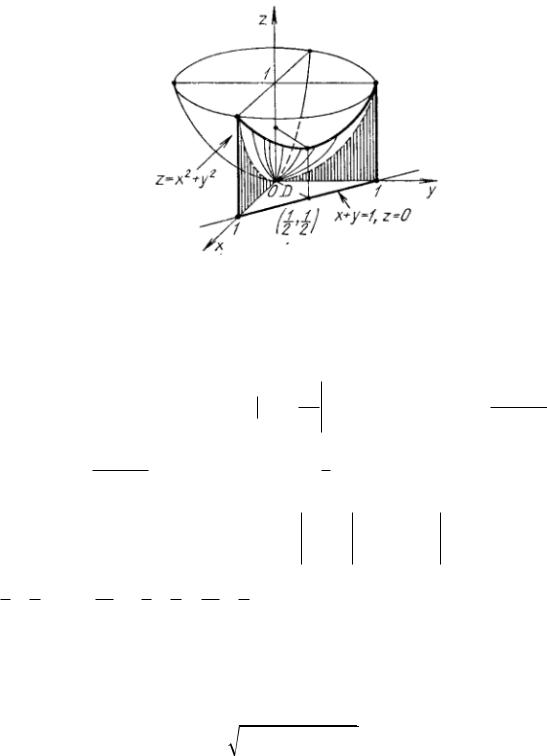
Пример 9.

верхностями

Решение.

Вычислить объем тела, ограниченного по-

x	2	y	2	,	x y 1,	x 0	,	y 0	,	z 0 .

Данное тело ограничено координатными

плоскостями

(параллельна оси


0 ,	y 0 ,	z 0 , плоскостью
Oz ) и параболоидом вращения			z x	2
Oz ) и параболоидом вращения			z x

y 1

												Рисунок 18 - Построение области																																						D
																1		1 x														1						1 x								1 x
			x							dxdy										x								dy
V					2	y			2								dx					2		y			2							dx						x	2	dy						y	2		dy
V						y											dx							y										dx						x		dy						y			dy
		D														0			0													0							0							0
	1					1 x				1 x									1														y		3	1 x					1											(1 x)	3
	1					1 x				1 x									1																3						1												3
					2			dy			y		2												x	2	y	1 x																			2	(1 x)
dx x								dy			y				dy dx										x		y													dx x								(1 x)
																												0				3																				3
	0					0					0								0													3				0					0											3
																																				0
	1									(1 x)				3						1								1								1		1
										(1 x)																										1
			2	x			3																2	dx x					3		dx							(1 x)						3	dx
x				x												dx x								dx x							dx							(1 x)							dx

	0										3									0								0								3		0
	1					1						1	1																	x3 1							x4 1						(1 x)4 1
x2dx x3dx													(1 x)3 d (1 x)
x2dx x3dx												3	(1 x)3 d (1 x)																		3							4							12
	0					0						3	0																		3	0						4		0					12						0
																																0								0											0
	1		1							1				1				1			1					1	.
				0																							.
	3		4							12				3				4		12						6

3. Вычисление площади поверхности

Если поверхность задана уравнением

(x;

, то пло-

щадь части поверхности вычисляется по формуле

S 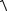1 (zx' )2 (z'y )2 dxdy .

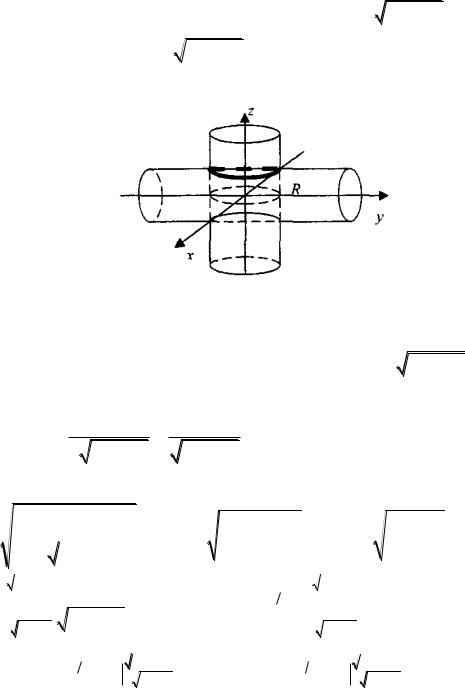
Пример 10. Найти площадь поверхности тела, образованного перпендикулярным пересечением двух цилиндров

одинакового радиуса

R .

Решение. Уравнение

двух

перпендикулярных цилин-

дров имеют вид:

. Первый из них

определяет область интегрирования D :

y	R	2	x	2
		2		2

, а вто-

рой – поверхность мо вычислить.

z	R	2	x	2
		2		2

, площадь которой необходи-

Рисунок 19 - Построение области

Найдем

площадь

верней части тела:

этого найдем частные производные:

zx (x const)

zx ( y const) 0 .

Тогда получим

, для

dxdy

R2 x2

dy R (R2

x2 ) 1 2 dx

R2 x2

R (R2 x2 ) 1 2 dx y

(R2 x2 ) 1 2 dx y

R2 x2

2R (R2 x2 ) 12 (R2 x2 )12 dx 2R dx 2R x RR 2R(R R) 4R2 .

R R

Площадь верхней части тела	4R	2	. Все тело состоит из

четырех таких частей, поэтому площадь всей поверхности

равна:	S 16R	2	.

4. Вычисление массы плоской пластинки

Масса плоской пластинки D	с переменной плотностью
(x; y) находиться по формуле
m (x; y)dxdy – в декартовых координатах,
D

m (r cos ;r sin )rdrd D

– в полярных координатах.


Пример 11. Пластинка D			задана ограничивающими ее
кривыми: y2 5x , x 5 , y 0 ,			( y 0 ). Поверхностная плот-
ность равна 2x 3y	2	. Найти массу пластинки.

Решение. Изобразим пластинку на рисунке

Рисунок 20 - Построение области

							5				5x								5						5x		5x

m		(x; y)dxdy							dx			(2x 3y			2	)dy				dx						2xdy		3
m		(x; y)dxdy							dx			(2x 3y				)dy				dx						2xdy		3
	D						0				0								0						0		0

																							3			5x
5				5x	5x								5										3			5x
								2									5x				y
								2									5x				y
													dx 2x y 0
dx			2x	dy 3 y dy									dx 2x y 0						3			3
0				0	0								0									3			0

5											5								5
dx 2x										7x
dx 2x				5x 5x		5x				7x				5xdx 7				5 x						xdx

	2
y	2	dy
y		dy

0						0
	5				x	5 / 2	5
	5					5 / 2
7	5 x	3/ 2	dx 7	5			7 5
		3/ 2
	0				5/ 2		0
	0

	Пример 12. Пластинка
кривыми:			x2 y2 16,				x2 y2

2 5	5 / 2	7	5 2 25 5
				350 .
5			5

D задана ограничивающими ее
25 , x 0 ,			y 0 , ( x 0 , y 0 ). По-

верхностная плотность равна	3x y				. Найти массу пла-
	x	2	y	2

стинки.

Решение. Изобразим пластинку на рисунке

Рисунок 21 - Построение области

Перейдем в двойном интеграле к полярным координа-

там

x r cos

y r sin


	2	5		r(3cos sin )								2	5	r(3cos sin )
m (x; y)dxdy d				r(3cos sin )							rdr	d		r(3cos sin )	dr
m (x; y)dxdy d			r	2	2	r	2	sin	2		rdr	d		r	dr
D	0	4	r		cos	r		sin				0	4	r
D	0	4										0	4

2		5
(3cos sin )d dr (3sin cos ) 02										3 1 2 .
0		4
5.	Вычисление статических моментов и координат

центра тяжести плоской фигуры.

Статические моменты пластины D относительно осей Oy вычисляются по формулам

Sx y (x; y)dxdy	и Sy x (x; y)dxdy ,
D	D

а координаты центра масс фигуры – по формулам

xc Sy и yc Sx . m m

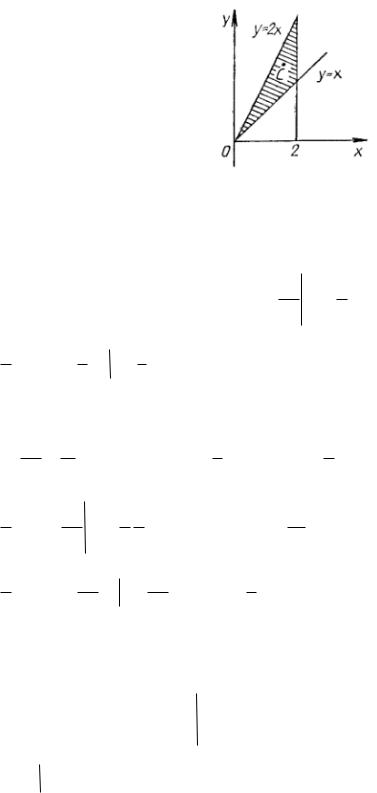
Пример 13. Найти координаты центра масс пластинки

D y

лежащей в плоскости	Oxy	и ограниченной линиями
2x , x 2, если ее плотность (x; y) xy .
Решение.

Рисунок 22 - Построение области

Вначале определим массу пластинки

								2	2 x
m (x; y)dxdy dx xydy
		D						0	x
	3	2		3			2	3
	3	3	dx	3	x	4	2	3	(16 0)
	2	x	dx	8	x		0	8	(16 0)
	2	0		8			0	8
		0

2	y	2	2 x	1	2

xdx					x(4x	2	x	2	)dx

	2			2
0			x		0

Определим координаты центра масс:

				S						1																1										1		2			2 x
c				S			y			1					x			(x; y)dxdy								1					2					1			2				ydy
x					m					m					x			(x; y)dxdy								6				x			ydxdy			6			x		dx		ydy
					m					m			D													6		D								6		0				x
													D															D										0				x
		1	2								y	2	2 x					1 1			2													3	2
			2									2									2														2
							2	dx													x	2	(4x		2	x			2	)dx						4		dx
		6	x					dx			2							6 2			x		(4x			x				)dx				12	x			dx
		6	0								2		x					6 2			0													12	0
			0										x								0														0
		1	2										1					2			1									8
		1					4	dx					1			x	5	2			1	(32 0)								8			,
							4										5
					x
		4	0										20					0			20									5
			0																																		6
						m					m															6											6
y						Sx					1					y (x; y)dxdy											1				yxydxdy						1			xy2dxdy
y																y (x; y)dxdy															yxydxdy									xy2dxdy
		c
													D																D										D
		1	2						2 x										1	2			y3	2 x					1 1				2									7		2
			2						2 x											2													2											2
			xdx y2dy																	xdx												x(8x3 x3 )dx												x4dx

		6																	6				3						6 3													18
		6	0						x										6	0			3	x					6 3				0									18		0
			0						x											0				x									0											0
		7		x5				2				7		(32 0)								112		.
	18			x5				2			90			(32 0)										.
	18							0			90											45

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.01.20243.7 Mб02021_077.pdf
#
01.01.2024692.06 Кб02021_078.pdf
#
01.01.20243.03 Mб02021_079.pdf
#
01.01.20244.02 Mб02021_080.pdf
#
01.01.20241.76 Mб02021_081.pdf
#
01.01.20243.23 Mб02021_082.pdf
#
01.01.20241.23 Mб12021_083.pdf
#
01.01.20241.8 Mб02021_084.pdf
#
01.01.20241.3 Mб02021_085.pdf
#
01.01.20244.75 Mб02021_086.pdf
#
01.01.20244.82 Mб12021_087.pdf