2021_082

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский Государственный аграрно-технологический университет им. Д.Н. Прянишникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

где величину f (x ; y ; z )

f (x; y; z)dV называют средним

где величину f (x ; y ; z )

f (x; y; z)dV называют средним

значением функции f (x, y; z)

в области V .

.pdf

Скачиваний:

Добавлен:

01.01.2024

Размер:

3.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

6. Вычисление моментов инерции точки.

Моменты инерции относительно начала координат и

осей координат

материальной пластины

с непре-

рывно распределенной поверхностной плотностью (x; y) , вычисляются по формулам:

2

(x	2	y	2
	2		2
D
(x; y)dxdy ,

) I y

(x; y)dxdy ,
x	2	(x; y)dxdy
	2
D

Пример 14. Вычислить моменты инерции относительно точки границы однородного круга и его диаметра, если радиус круга R , а вес P .

Решение. Поместим начало координат в точке, лежащей на границе круга, а центр круга – в точке C(R;0) .

Тогда задача сведется к нахождению моментов инерции круга относительно начала координат и оси Ox .

Рисунок 23 - Построение области

Так как круг однороден, то его плотность постоянна

P
и g R2	. Уравнение окружности в декартовой системе ко-

ординат имеет вид: (x R)2 y2 R2 .

I0 (x2 y2 )dxdy .

Сначала преобразуем подынтегральное выражение x2 2xR R2 y2 R2 или x2 y2 2xR .

Перейдя к полярным координатам:

r	2	2	r	2	sin	2	2rRcos
		cos

Имеем

или

2Rcos

I0	(x											y						)dxdy												2	d					2R cos										(r				cos							r					sin					)rdr
I0	(x									2		y				2		)dxdy													d															(r		2		cos					2		r				2	sin				2	)rdr
										2						2																																2							2						2					2
					D																									2										0
			2						2R cos																			2					r		4				2R cos																			2
			2						2R cos																			2							4																							2
						d											r		3	dy										d																		4 R										4			cos				4	d
						d											r			dy										d																		4 R													cos					d

				2								0																2						4					0																					2
				2								0																2											0																					2
						2																									2			1 cos 2																			2
4 R					4						cos				4		d 8 R												4					1 cos 2																				d
4 R											cos						d 8 R																										2											d
									2																					0													2
									2																					0
									2											2														2		1			cos 4
2 R				4				d									2 cos 2 d																			1			cos 4												d
2 R								d									2 cos 2 d																																		d

								0												0												0												2
								0												0												0
				4																	1						1													2												4												3
2 R				4			sin 2														1						1	sin 4																		2 R						4												3		R			4
2 R							sin 2														2						8	sin 4																		2 R									2									2		R
																					2						8											0																	2				4					2
																																						0
	3			P					R					4					3 P				R		2	.
									R														R			.

	2 g R							2											2 g
	2 g R																		2 g
																								2				2R cos																														2										r	4	2R cos
																								2				2R cos																														2											4
Ix	y								2		dxdy														d									r			3		sin						2	dr														sin			2	d
									2																												3								2																		2
					D																2									0																													2									4		0
					D																2									0																													2											0
						2																																				2		1												1 cos 2
4 R					4						cos				4		sin					2		d 8 R													4							1		sin				2		2				1 cos 2										d
4 R											cos						sin							d 8 R																						sin						2														d

									2																															0				4																2
									2																															0
R						2							2 d R																2						2 cos 2 d
R		4						sin				2	2 d R														4			sin			2		2 cos 2 d
		4										2															4						2
						0																						0
	R		4				2																									sin						3		2							2
			4				2																															3
						(1 cos 4 )d R																									4
																															4
	2					0																																6								0
						0																																								0
	R4											1											2																		1 P
	R4											1																						4							1 P								2
														sin 4																R																	R				.
														sin 4																R																	R				.
	2											4											0					4													4 g
																							0
																Задачи для самостоятельного решения
			1. Вычислить площадь фигуры, ограниченной кривыми
xy 4 ,							x y 5 0 . (Ответ:																											27						4ln 4 .)
xy 4 ,							x y 5 0 . (Ответ:																													2				4ln 4 .)
																																				2

2. Вычислить площадь фигуры, ограниченной кривыми

y	2

2



4 y 3

x
	2
3	.)

y	2

8y x2

x /

(Ответ:


3.	Вычислить объем тела, ограниченного поверхностями
x2 y2 z 1 0, x2 y2 3z 7 0. (Ответ:						2	.)
x2 y2 z 1 0, x2 y2 3z 7 0. (Ответ:							.)
					3
4.	Вычислить площадь части конуса y 2							x	2	z		2		, рас-
4.	Вычислить площадь части конуса y 2							x		z				, рас-
положенной внутри цилиндра x		2	z	2	4x . (Ответ: 4						5		.)
положенной внутри цилиндра x			z		4x . (Ответ: 4						5		.)
5.	Найти массу материальной				пластинки,			лежащей в

координаты центра масс однородной плоской фигуры, лежа-

щей в плоскости	Oxy	и ограниченной линиями	у	2	4х 4	,

у	2

2х

. (Ответ:

 

2 5

7. Вычислить моменты инерции относительно координат и осей координат пластины плотностью лежащей в плоскости Oxy и ограниченной линиями

начала

х	2	у		,

у х			2	,

. (Ответ:

104	,	I x	4	,	I y	4	.)
495			33			45

Вопросы для самоконтроля

1.Как вычисляется площадь в декартовых координа-

тах?

2. Как вычисляется площадь в полярных координа-

тах?

3.Как вычислить объем тела через двойной инте-

грал?

4.Как вычисляется масса пластинки в декартовых координатах?

5.Как вычисляется масса пластинки в полярных координатах?

6.Как найти центр тяжести плоской фигуры?

3.2 Теоретический материал по тройным интегралам

3.2.1 Определение тройного интеграла

Обобщением определенного интеграла на случай функции трех переменных является так называемый тройной интеграл. Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращен-

ном виде.
Пусть в замкнутой области V	пространства	Oxyz задана
непрерывная функция u f (x, y, z) .
Разбив область V сеткой поверхностей на		n частей Vi

(i 1,...,n ) и выбрав в каждой из них произвольную точку

M	(x	;
i	i

y ; z	i
i

)

составим интегральную сумму

n
	f (x	; y	; z	) V
	i	i	i	i
i 1

для функции

f (x, y

ментарной области

, z)	по области
Vi ).

(здесь

- объем эле-

	n
Определение 4. Сумма вида f (M i ) Vi		называется ин-
	i 1
тегральной суммой для функции	f (x, y, z) в области V .

Определение 5. Если существует один и тот же предел интегральных сумм при n и 0 , не зависящий ни от способа разбиения области V на части, ни от выбора точек

M i	в них, то он называется тройным интегралом от функ-
ции f (x, y, z) по области V и обозначается
			n
	f (x; y; z)dxdydz lim		f (xi ; yi ; zi ) Vi f (x; y; z)dV .
	V	n	i 1	V
		0
	В этом случае функция		f (x, y, z)	называется интегрируе-

мой в области V , область V – областью интегрирования, x , y и z – переменными интегрирования, dV dxdydz – эле-

ментом объема.

Теорема 3 (существования тройного интеграла). Если

подынтегральная функция

f (x, y, z)

непрерывна в каждой

точке простой замкнутой области V , то она в этой области интегрируема. (Без доказательства).

Свойства тройного интеграла

Тройной интеграл обладает теми же свойствами, что и

двойной интеграл:
1. dV V , так как	в случае f (x, y, z) 1 любая инте-

гральная сумм имеет вид

n
	i	V
	V	V
i 1

и численно равна объему

тела.

2.		cf (x; y; z)dV
2.		cf (x; y; z)dV
	V

c V

f (x; y; z)dV

c const

( f1 (x; y; z) V

f2 (x; y; z))dV V

f1 (x; y; z)dV V

f	2	(x; y; z)dV
	2

4.		f (x; y; z)dV			f (x; y; z)dV f (x; y; z)dV ,					если
			V	V		V
				1		2
V1 V2 V , а пересечение V1					и V2	состоит из границы, их раз-
деляющей.
5.	f (x; y; z)dV 0 ,				если	в области		V	функция
	V
f (x, y; z) 0		.	Если	в		области	интегрирования
f (x, y; z) (x; y; z) , то и				f (x; y; z)dV (x; y; z)dV .
			V			V

6. Оценка тройного интеграла

mV V

f (x; y; z)dV

где

ние

m и M соответственно наименьшее и наибольшее значефункции f (x, y; z) в замкнутой области V .

7. Если функция сти V , объем которой

точка M0 (x0 ; y0 ; z0 ) , что

f (x, y; z) непрерывна в замкнутой обла- V , то в этой области существует такая

f (x; y; z)dV f (x0; y0; z0 )V ,

3.2.2 Вычисление тройного интеграла в декартовой системе координат

Процедура вычисления тройного интеграла аналогична соответствующей операции для двойного интеграла. Для ее описания введем понятие правильной трехмерной области.

Определение 6. Трехмерная область V	, ограниченная
замкнутой поверхностью S , называется правильной в
направлении оси Oz , если:
1) любая прямая, параллельная оси Oz	и проведенная
через внутреннюю точку области, пересекает	S в двух точ-
ках;
2) вся область V проектируется на плоскость Oxy в пра-

вильную двумерную область D;

3) любая часть области V , отсеченная от нее плоскостью, параллельной какой-либо из координатных плоскостей,

обладает свойствами 1) и 2).
Пусть	областью интегрирования V		-	является тело,
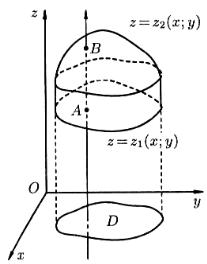
ограниченное снизу поверхностью		z z1 (x; y) , сверху – по-
верхностью	z z2 (x; y) , причем	z z1 (x; y)		и	z z2 (x; y)

( z1 (

сти

x; y) D ,

z1 (x; y) ) – непрерывные функции в замкнутой являющейся проекцией тела на плоскость Oxy .

обла-

Рисунок 24 - Правильная область в направлении оси Oz

Если область V - правильная в направлении оси

то для любой непрерывной в области V функции f (x,

Oz , y; z)

имеет место формула

		z2		( x; y)
	f (x; y; z)dV			f (x; y; z)dz dS
			1
V	D			( x; y)
			z

сво-

дящая вычисление тройного интеграла к вычислению двойного интеграла от однократного.

Сначала вычисляется внутренний интеграл по переменной z при постоянных x и y в пределах изменения z .

Нижней границей интеграла является аппликата точки A – точки входа прямой, параллельной оси Oz в область V , т.е. z z1 (x; y) ; верхней границей – аппликата точки B - точки выхода прямой из области V , т.е. z z2 (x; y) . Результат вычисления этого интеграла есть функция двух переменных x и y .

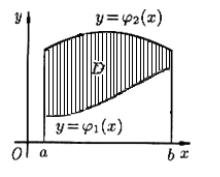
Пусть область D ограничена линиями x a , x a ( a b ), y 1 (x) и y 2 (x) , где 1 (x) и 2 (x) – непрерывные на отрезке [a;b] функции, причем 1 (x) 2 (x) .

Рисунок 25 - Расстановка границ интегрирования

Тогда при переходе от двойного интеграла по области D к повторному получаем формулу вычисления тройного интеграла в декартовых координатах

	b	2	( x) z2		( x; y)
	f (x; y; z)dV dx		dy		f (x; y; z)dz .
V	a	1 ( x)		z1 ( x; y)

При этом пределы интегрирования расставляются последовательно: «от точке к точке», «от линии к линии», «от поверхности к поверхности».

Если область V более сложная, чем рассмотренная, то ее следует разбить на конечное число правильных областей, к которым можно применить полученную формулу.

Пример 15. Вычислить (2x y z)dxdydz , если область

V z

ограничена поверхностями

2 .

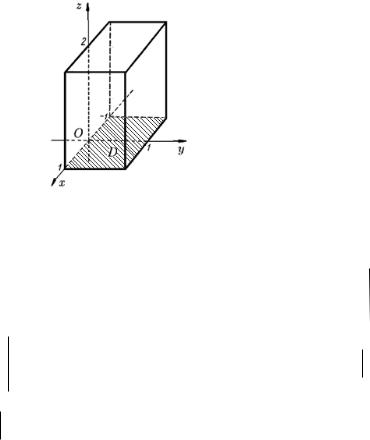
Решение. Строим область интегрирования

Рисунок 26 - Построение области V

		1		1	2	1	1		z2		2
									z2

(2x y z)dxdydz dx dy (2x y z)dz dx dy								2xz yz
(2x y z)dxdydz dx dy (2x y z)dz dx dy								2xz yz	2
V		1		0	0	1	0		2	0
1	1	z2	2	1	1		1			1
		z2								1

dx dy 2xz yz				dx (4x 2 y 2)dy dx (4xy y2 2 y)
dx dy 2xz yz				dx (4x 2 y 2)dy dx (4xy y2 2 y)
1	0	2 0		1	0		1			0
1	0	2 0		1	0		1

1
	(4x 1)dx (2x	2
	(4x 1)dx (2x
1

	x)	1
	x)	1
		1

2(1 1) (1 1)

Пример 16. Вычислить

(2x y)dxdydz , если область

ограничена поверхностями	y x ,
z 1 x2 y2 .

y 0 ,

z 1,

Решение. Строим область интегрирования V

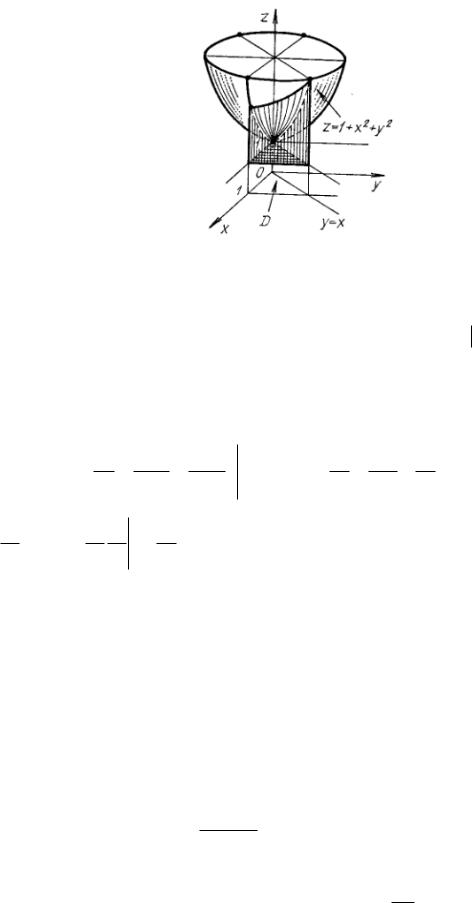
Рисунок 27 - Построение области

	1	x		2	y	2	1	x
	1	x	1 x		y		1	x	2	y	2
(2x y)dxdydz dx dy							(2x y)dz dx (2x y)dy z		1 x	y
(2x y)dxdydz dx dy							(2x y)dz dx (2x y)dy z		1
V	0	0		1			0	0
1	x			1	x

dx (2x y)(x2 y2 )dy dx (2x3 y3 2xy2 x2 y)dy

0 0

1					y		y	4
dx 2x				3	y
				3
0							4
41	1					41 x			5
41	x	4	dx			41 x
		4
21						21 5
21	0					21 5
	0

						0			0
			3			2		2		x	1				4		4		4
2xy			3		x	2	y	2			1			x	4	2x	4	x	4
2xy					x		y					2x		x		2x		x
												2x	4							dx
													4
	3					2				0	0			4		3		2
										0
1		41
		41		.
		60		.
0		60
0

Задачи для самостоятельного решения

(x; y;

Расставить пределы интегрирования		в интеграле
z)dxdydz , если область V	ограничена	плоскостями

0	, y 0, z 0	,	2x 3y 4z 12
	2. Расставить пределы
f (x; y; z)dxdydz		,	если область

интегрирования в интеграле

V	ограничена поверхностями

y х ,

у 2х ,

x z 2

3. Вычислить 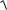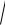х2

у 2 dxdydz , если область V ограни-

чена поверхностями z 1, z x2 y2 .(Ответ: 415 .)

M (x; y; z)

Вопросы для самоконтроля

1.Что называется тройным интегралом?

2.Какие свойства тройных интегралов вы знаете?

3.Как расставляются границы интегрирования в тройном интеграле?

3.2.3 Замена переменных в тройном интеграле

При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т.е. совершается пре-

образование переменных.
Пусть совершена подстановка	x (u;v; w) ,	y (u;v; w) ,
z (u;v;w) .
Если эти функции имеют в некоторой области V			про-
Если эти функции имеют в некоторой области V			про-

странства Ouvw непрерывные частные производные и отличный от нуля определитель

	x	x
	u	v
J (u;v; w)	y	y
J (u;v; w)	u	v
	u	v
	z	z
	u	v

то справедлива формула замены переменных в тройном интеграле:

f (x; y; z)dV f ( (u;v; w); (u;v; w); (u;v; w)) J (u;v; w) dudvdw .

Здесь J (u;v; w) - определитель Якоби, или якобиан преобразования.

Вычисление тройного интеграла в цилиндрических координатах

Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты. Положение точки в пространстве Oxyz можно определить зада-

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.01.20243.7 Mб02021_077.pdf
#
01.01.2024692.06 Кб02021_078.pdf
#
01.01.20243.03 Mб02021_079.pdf
#
01.01.20244.02 Mб02021_080.pdf
#
01.01.20241.76 Mб02021_081.pdf
#
01.01.20243.23 Mб02021_082.pdf
#
01.01.20241.23 Mб12021_083.pdf
#
01.01.20241.8 Mб02021_084.pdf
#
01.01.20241.3 Mб02021_085.pdf
#
01.01.20244.75 Mб02021_086.pdf
#
01.01.20244.82 Mб12021_087.pdf

						0			0
			3			2		2		x	1				4		4		4
2xy			3		x	2	y	2			1			x	4	2x	4	x	4
2xy					x		y					2x		x		2x		x
												2x	4							dx
													4
	3					2				0	0			4		3		2
										0
1		41
		41		.
		60		.
0		60
0

						0			0
			3			2		2		x	1				4		4		4
2xy			3		x	2	y	2			1			x	4	2x	4	x	4
2xy					x		y					2x		x		2x		x
												2x	4							dx
													4
	3					2				0	0			4		3		2
										0
1		41
		41		.
		60		.
0		60
0

						0			0
			3			2		2		x	1				4		4		4
2xy			3		x	2	y	2			1			x	4	2x	4	x	4
2xy					x		y					2x		x		2x		x
												2x	4							dx
													4
	3					2				0	0			4		3		2
										0
1		41
		41		.
		60		.
0		60
0