2021_082

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский Государственный аграрно-технологический университет им. Д.Н. Прянишникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

f (x; y)dxdy

f (x; y)dy .

f (x; y)dxdy

f (x; y)dy .

.pdf

Скачиваний:

Добавлен:

01.01.2024

Размер:

3.23 Mб

Скачать

☆

<<< < Предыдущая 12 / 82 3 4 5 6 7 8 > Следующая >>>

f (x, y)

Область, правильную (простую) в направлении обеих осей, будем называть правильной.

Рисунок 7 - Правильная область (в направлении обеих осей)

Пусть

(x; y)dxdy

требуется , где функция

вычислить двойной интеграл (x; y) 0 непрерывна в области D .

Положим сначала, что область						D представляет собой
правильную в направлении оси					Oy	область, ограниченную
прямыми	x a	и	x b	и кривыми	y 1 (x) и y 2		(x) , причем
функции	1 (x)	и	2 (x)	непрерывны и таковы, что			1 (x) 2 (x)
для всех	x [a;b] .

Рисунок 8 - Расстановка границ интегрирования

Данная формула представляет собой формулу вычисления двойного интеграла в декартовых координатах. Правую часть формулы называют двукратным (или повторным) интегралом от функции по области D .

При этом

лом.

2 ( x )

f (x; y)dy

	( x )
1

называют внутренним интегра-

Для вычисления двукратного интеграла сначала берем

внутренний интеграл, считая

постоянным, затем берется

внешний интеграл (результат первого интегрирования) по

x в

пределах от a до b , т.е. внешнее интегрирование производится «от точке к точке», а внутреннее - «от линии к линии».

Если же область D ограничена прямыми									y c	и y d
( c d ), кривыми x 1 ( y)	и	x 2 ( y) , причем 1						( y) 2		( y) для
всех y [c;d ], т.е. область	D	– правильная в направлении оси
				d			( x )
						2
Ox , то формула примет вид:			f (x; y)dxdy		dy				f (x; y)dx .
Ox , то формула примет вид:			f (x; y)dxdy		dy				f (x; y)dx .
		D		c			( x )
						1

При вычислении внутреннего интеграла считаем стоянным.

по-

Замечания:

1. Полученные формулы справедливы и в случае, когда

(x; y)

(x;

y) D

2. Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять по любой из полученных формул.

3. Если область D не является правильной ни по x , ни по y , то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси Ox или оси Oy .

4. Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.

f y


	Пример 1.		Записать двойной интеграл	от функции
(x, y) по области			D , ограниченной прямой y x	и параболой
x	2	, в виде повторных интегралов двумя способами.
x		, в виде повторных интегралов двумя способами.

Решение. Изобразим область

Рисунок 9 - Построение области

Так как область

– правильная по осям

Oy , то

двойной интеграл можно представить в виде повторного с

внутренним интегралом как по

x , так и по

y . Рассмотрим оба

случая:

1. Берем внутренний интеграл по

y , считая

постоян-

ным, а внешний интеграл – по	x . Область D находится в по-
лосе между прямыми x 0 и	x 1, следовательно, 0 x 1.

Чтобы найти пределы изменения для

y , возьмём на оси

произвольную точку

x (0;1)

и проведём через неё прямую,

параллельную оси Oy в направлении этой оси. Она пересека-

ет границу области D : ордината входа y x						2	,	а ордината вы-
ет границу области D : ордината входа y x							,	а ордината вы-
хода – y x , т.е.	x	2	y x . Тогда получим
хода – y x , т.е.	x		y x . Тогда получим
				1	x
			f (x; y)dxdy dx f (x; y)dy .
			D	0	x2
2. Берем внутренний интеграл по переменной x , считая
y постоянным,	а внешний – по			y .	Область			D находится в


полосе между прямыми y 0 и y 1,		следовательно, 0 y 1.
Чтобы найти пределы изменения для		x , возьмём на оси Oy
произвольную точку	y (0;1) и проведём через неё прямую,
параллельную оси Ox	в направлении этой оси. Она пересека-

ет границу области

D : абсцисса входа

x y , а абсцисса вы-

хода –

y , т.е.

y x

y . Тогда получим

1 f (x; y)dxdy dy

y
	f
y

(x; y)dx

Пример 2. Изменить порядок интегрирования в повтор-

ном интеграле

1	e
dx
0	e	x

(x;

y)dy

e	x
	x

ями

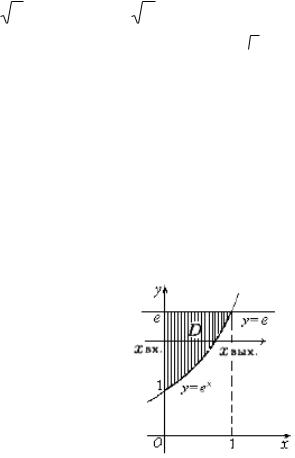
Решение.

y e , тогда
y e	x	и	y
	x

Внешний интеграл:

область интегрирования e

x D

1, внутренний – ограничена лини-

Рисунок 10 - Построение области

Из рисунка видно, что область D является правильной как в направлении оси Оx , так и в направлении оси Оy . В условии задачи, интеграл представлен в виде повторного с внутренним интегралом по переменной y , необходимо представить его по переменной х .

Для этого выразим переменную			х	, т.е.	y e	x	x ln y .
Для этого выразим переменную			х	, т.е.	y e		x ln y .
1	e	e	ln y
dx f (x; y)dy dy f (x; y)dx .
0	ex	1	0

Пример 3. Изменить порядок интегрирования в повтор-

ном интеграле

1	2 x
dx			f
0	x	2

(x; y)dy

ями

Решение. Область интегрирования D ограничена лини-

x 0	,	x 1,	y х	2	и	y 2 x . Получаем

Рисунок 11 - Построение области

Из рисунка видно, что область

является правильной в

направлении оси Оx , в направлении оси Оy область не является правильной. В условии задачи, интеграл представлен в виде повторного с внутренним интегралом по переменной y ,

необходимо представить его по переменной х .	Для этого
выразим из каждого уравнения переменную	x , т.е.

x 2 y .

прямой y 2 , 0

у1

на y .

две области D1 : В результате, по-

1	2 x			1
dx			f (x; y)dy dy
0	x	2		0

y
	f (x; y)dx
0

1	2 y
dy	f
0	0

(x;

y)dx

Пример 4. Область D ограничена следующими линия-

		y	3x2
ми:			3x2	,	y 3 x . Вычислить двойной интеграл
ми:			8	,	y 3 x . Вычислить двойной интеграл
			8
x2
		2 y dxdy .
	3	2 y dxdy .
D	3

Решение. Строим область D

Рисунок 12 - Построение области

Так как область

– правильная по осям Ox и Oy , то

двойной интеграл можно представить в виде повторного с

внутренним интегралом как по																																	x , так и по															y .

	x2															4				3 x					x2											4				3			x	x2									3 x
					2 y dxdy										dx														2 y			dy dx																dy						2 ydy
		3			2 y dxdy										dx												3		2 y			dy dx												3				dy						2 ydy
		3																					2				3																2	3											2
D																0					3x															0					3x													3x
																						8																			8												8
																																														3			x
	4				2 3	x										3	x										4				2													2		3			x
	4			x	2 3	x										3	x										4	x			2			3		x							y	2
dx				x					dy 2								ydy											x				y		3		x			2				y
dx									dy 2								ydy									dx						y		3x		2			2										2
	0			3 3x2												3x2											0			3				3x									2			3x			2
	0			3 3x2												3x2											0			3					8								2			3x
																																			8												8
						8											8																														8
						8											8
	4				2													2							3							3x		2			2
dx			x				3						x			3x												2				3x
dx							3						x														x
				3													8																8
	0			3													8																8

	4							x			4									9x			4						4										4						17					4
			2		x			x							9x					9x									x		5 / 2				9 xdx										17					x		4
		x																								dx							dx																				dx
		x							8											64						dx							dx												64								dx
	0								8											64									0										0						64					0
	x	7 / 2		4						x		2		4			17					x		5		4		2		4	7 / 2				9 16							17					4		5
		7 / 2										2												5							7 / 2																		5
					9
	7 / 2				9						2						64					5								7								2					64				5
	7 / 2			0							2			0			64					5				0				7								2					64				5
				0										0												0
	x	7 / 2		4						x		2		4			17					x		5		4		2		4	7 / 2				9 16							17					4		5
		7 / 2										2												5							7 / 2																		5
					9
	7 / 2				9						2						64					5								7								2					64				5
	7 / 2			0							2			0			64					5				0				7								2					64				5
				0										0												0
	256			72						17 16									1280 2520 272																				3528						504						.
				72																																															.
		7												5													35												35								5
																																		16

Пример 5. Вычислить

xydxdy

, где область

ограни-

чена линиями Решение.

сунке.

y x	2	,	y 0	,	x y 2 0 .

Область интегрирования

изображена на ри-

Рисунок 13 - Построение области

Она правильная в направлении оси Ox . Необходимо вы-

разим из каждого уравнения переменную

x , т.е.

2	x	y и x y 2 0	x 2
2

Воспользуемся формулой:

									2		2 y							2	2 y						2		2 y
xydxdy dy													xydx dy xydx ydy															xdx
D									1				y					1		y					1			y
	2				x				2		2 y				2		(2 y)						2		y		2		4 4 y y		2	y
	2								2						2								2				2				2
ydy														ydy												y							dy
							2												2										2
	1						2				y				1				2					2			1		2
											y							1						5
	2		y			2	5y 4											1	2					5	2				2
y																			y	3	dy				y	2	dy 2 ydy
y															dy				y	3	dy				y	2	dy 2 ydy
	1									2								2	1					2	1				1
	1	y4		2				5			y3	2 2				y2	2 2					1		5	8 1 4 1 5					1			35	23	.
				2								2 2					2 2								8 1 4 1 5										.
	2 4 1						2 3 1								2 1							8		6						8			6	24

Задачи для самостоятельной работы:

1. Представить двойной интеграл в виде повторного ин-

теграла, если область D ограничена линиями y 2x ,	у 3 х ,
x 0 .

2. Изменить порядок интегрирования в повторных интегралах:

2 x

1 y

а) dx f (x; y)dy ; б) dy

f (x; y)dx ;

1 y2

в)

f (x; y)dy

f (x; y)dy .

2. Вычислить двойной интеграл по области

D :

а)

xdxdy , если область

ограничена линиями

x	2

y 2х			. (Ответ:			4	.)
y 2х			. (Ответ:			3	.)
		б)		x		3	если область
		б)		x	dxdy ,		если область
				2
				D
y	1	,	x 2. (Ответ:					9	.)
								9
	x							4
								4

ограничена линиями

в)

г)

xdxdy

если область

ограничена линиями

, y 0

0 . (Ответ:

(2ху 16x

)dxdy , если область D ограничена лини-

ями y x3 , x 1,

y	x . (Ответ: 5	.)
	8

Вопросы для самоконтроля

1.Что называется двойным интегралом?

2.Какие свойства двойных интегралов вы знаете?

3.Какая фигура называется правильной в направле-

нии оси

Ох

4.Какая фигура называется правильной в направлении оси Оу ?

5.Какая фигура называется простой или правильной?

6.Как расставляются границы в повторном интегра-

ле?

3.1.3 Замена переменных в двойных интегралах

Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.

Пусть вычисляется двойной интеграл			f (x; y)dxdy .

	D
Теорема 2 (о замене переменных в двойном интегра-
ле). Пусть на плоскости Ouv задана область				, и пусть отоб-
		D
ражение F преобразует эту область в область				D на плоско-

сти Oxy , функции	x(u,v) , y(u,v) непрерывно дифференцируе-
мы на D (имеют непрерывные частные производные), яко-
биан
			x	y
	J (u,v)	(x, y)	u	u
			u	u
		(u,v)	x	y
		(u,v)	x	y
			v	v

не обращается в нуль на D .

f (x; y)dxdy f
D
	D

Тогда справедливо

(x(u,v); y(u,v)) J (u,v)

равенство: dudv . (*)

(Без доказательства)

Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат x и y полярными координатами r и .

Полярные координаты

(r; )

связаны с декартовыми ко-

ординатами (x; y) следующими формулами:

x r cos

y r sin

Тогда якобиан преобразования имеет вид

	x	y
J (r, )	r	r	cos	r sin	r ,
	x	y	sin	r cos

Тогда формула (*) примет вид

	f (x; y)dxdy		f (r cos ;r sin )rdrd
D( x, y)		D(r, )

Для вычисления двойного интеграла в полярных координатах применяют то же правило сведений его к двукратному интегралу.

	Пусть область D		ограничена лучами	и , где

, и кривыми r r1 ( ) и r r2 ( ) , где r1 ( ) r2				( ) . Область
D	правильная: луч,	выходящий из полюса, пересекает ее

границу не более чем в двух точках.

Рисунок 14 - Полярная система координат Тогда формула примет вид:

D(r, )

	r	( )
f (r cos ;r sin )rdrd d	2
f (r cos ;r sin )rdrd d
	r ( )
	1

(r cos ;r sin )rdr

Внутренний интеграл берется при постоянном

Замечания.

1. Переход к полярным координатам полезен, когда подынтегральная функция имеет вид f (x2 y2 ) ; область D есть круг, кольцо или часть таковых.

2. На практике переход к полярным координатам осуществляется путем замены x r cos , y r sin , dxdy rdrd . Уравнение линий, ограничивающих область D , также преобразуются к полярным координатам. Преобразование области

<<< < Предыдущая 12 / 82 3 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.01.20243.7 Mб02021_077.pdf
#
01.01.2024692.06 Кб02021_078.pdf
#
01.01.20243.03 Mб02021_079.pdf
#
01.01.20244.02 Mб02021_080.pdf
#
01.01.20241.76 Mб02021_081.pdf
#
01.01.20243.23 Mб02021_082.pdf
#
01.01.20241.23 Mб12021_083.pdf
#
01.01.20241.8 Mб02021_084.pdf
#
01.01.20241.3 Mб02021_085.pdf
#
01.01.20244.75 Mб02021_086.pdf
#
01.01.20244.82 Mб12021_087.pdf