Сопромат Лекции Часть 1

ГЛАВА 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНОГО СЕЧЕНИЯ БРУС

5.4Главные оси инерции и главные моменты

инерции сечения

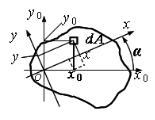
Изобразим поперечное сечение бруса и произвольные оси , . Выделим элементарную площадку (рис. 5.8, а) с координатами , .

Рис. 5.8. Схема поворота координатных осей

Поверн¼м оси на 90 , например, против часовой стрелки (рис. 5.8, б). Запишем зависимость между координатами 1 = − ; 1 = .

Вычислим центробежные моменты инерции сечения в осях , и 1, 1,:

Следовательно, при повороте осей на 90 центробежный момент инер-

ции сечения меняет знак на обратный.

Представим графически изменение центробежного момента инерции в зависимости от угла (рис. 5.9). Эта функция непрерывная (разрывов

нет). Если повернуть оси на угол 0, то попад¼м на оси, относительно которых = 0.

Рис. 5.9. График изменения при повороте осей

Итак, для любого начала координат имеется хотя бы одна пара осей, относительно которых центробежный момент инерции сечения равен нулю.

ГЛАВА 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНОГО СЕЧЕНИЯ БРУС

что и требовалось доказать.

5.5Зависимость между моментами инерции сечения при повороте от главных осей

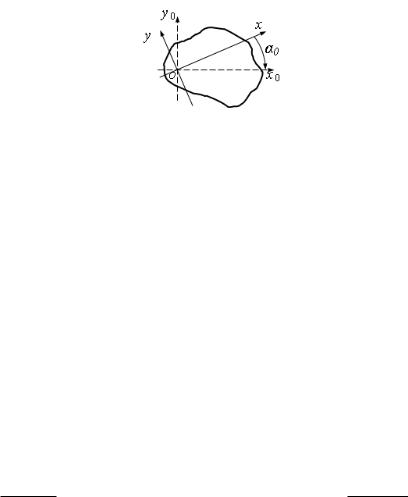
Изобразим произвольное сечение, любое начало координат и покажем главные оси 0, 0. 0 0 = 0 (ðèñ. 5.12).

Рис. 5.12. Определение моментов инерции при повороте от главных осей

Известны 0 , 0 . Необходимо определить , , . Положение осей , определяет угол (на рисунке показан положительный

угол). Выделим элемент сечения . Установим связь между координатами

= 2 · 0 + 2 · 0 ,

∫

òàê êàê 0 0 = 0 · 0 = 0. Аналогично получаем , .

ГЛАВА 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНОГО СЕЧЕНИЯ БРУС

Таким образом

= 0 · 2 + 0 · 2 ,

= 0 · 2 + 0 · 2 ,

= 0 − 0 · 2 2

формулы поворота от главных осей; эти формулы аналогичны формулам поворота от главных площадок в теории напряж¼нного и деформированного состояния.

Последняя формула отвечает на вопрос: сколько же главных осей имеет сечение? Одни главные оси есть и они показаны на рисунке. Если есть другие главные оси, то при повороте к ним

жительные и отрицательные целые числа и ноль. Тогда = 2 · , т.е. бесконечное множество корней. Если оси будем поворачивать на угол, кратный 2 , то будем попадать на прежние оси, правда изменятся направления осей, что в данном случае значения не имеет. Таким образом,

имеется одна пара главных осей.

2) 0 = 0 . В этом случае произведение обращается в ноль при любом и любые оси главные, т.е. имеется бесконечное множество

главных осей. Из формул, привед¼нных выше, получим в этом случае:

+ = 0 + 0 .

Примеры таких сечений (рис. 5.13):

Рис. 5.13. Сечения, имеющие бесконечное множество главных осей

а) круглое, но только тогда, когда начало координат находится в центре тяжести сечения ;

б) квадратное сечение начало координат находится в центре тяже- сти сечения , 0 = 0 , следовательно любые оси главные.

ГЛАВА 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНОГО СЕЧЕНИЯ БРУС

5.6Определение главных моментов и положения главных осей инерции сечения

Такая задача решается при расч¼те бруса на изгиб. Выше было рассмотрено решение прbменительно к симметричному сечению, а теперь привед¼м решение для произвольного сечения (рис. 5.14).

Рис. 5.14. Определение главных моментов инерции и положения главных осей

Известны , , . Эти характеристики можно определить численным методом, разбив сечение на отдельные части, или разбив сложное

сечение на простые составляющие. Требуется определить 0 , 0 , 0( 0 0).

Рассмотрим произвольное сечение и произвольные оси , . Главные

оси, которые следует найти, покажем штриховой линией.

Для решения поставленной задачи воспользуемся математической аналогией с формулой для напряжений.

Запишем вначале формулы, чтобы показать, что аналогия существу-

Сравниваем эти формулы они аналогичны. Из формул для напряжений можно получить формулы для моментов инерции, если заменить:

ГЛАВА 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНОГО СЕЧЕНИЯ БРУС

Таким образом поставленная задача решена. Из полученных формул следует замечательное свойство главных моментов инерции: один из них является наибольшим, а другой наименьшим, если рассматривать множество осей, проходящих через заданное начало координат (в арифметическом смысле).

5.7Исследование моментов инерции графическим способом

Так как между напряжениями и моментами инерции существует аналогия, то для определения моментов инерции можно использовать круги Мора.

Рассмотрим решение обратной задачи. Доказательство правомочно-

сти действий можно провести аналогично определению напряжений. Известно: , , . Нужно определить 0 , 0 , 0( 0). Изобразим

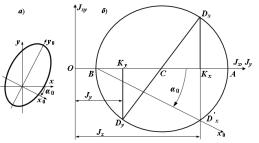
горизонтальную , и вертикальную оси. Необходимо обратить внимание на то, что ось , не имеет отрицательных значений. Покажем произвольное сечение с осями , (рис. 5.15).

Рис. 5.15. Круг Мора для определения моментов инерции

Строим точки ( , ) и ( , − ). Четв¼ртой величины в моментах инерции нет, но учт¼м, что = − . Пусть > ; это условие необязательно, но для выбранного сечения это так. В рассматриваемом случае также > 0. Далее соединяем точки , и получаем центр окружности . Зная центр и радиус = проводим круг Мора для моментов инерции и определяем

ГЛАВА 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНОГО СЕЧЕНИЯ БРУС

Далее нужно определить угол 0. Строим точку ′ , симметричную точке относительно оси абсцисс. Из точки через точку ′ прово-

дим луч . Это и есть направление оси 0, относительно которой момент

инерции будет наибольшим.

Прямую задачу проработать самостоятельно. Дано 0 , 0 , ( 0 ). Требуется определить , , .

5.8Эллипс инерции

Введ¼м новое понятие понятие о радиусе инерции сечения. Изобразим произвольное сечение и любую ось (рис. 5.16).

Рис. 5.16. Определение радиуса инерции относительно произвольной оси

Отсюда = 2 · . Эта формула для определения не используется, но ряд формул сопротивления материалов, где сокращается площадь, можно записать проще.

главные радиусы инерции сечения или радиусы инерции сечения относително главных осей.

Эллипсом инерции называется эллипс, имеющий следующее уравнение в главных осях (рис. 5.17):

.

ГЛАВА 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНОГО СЕЧЕНИЯ БРУС

Рис. 5.17. Эллипс инерции

Полуосями эллипса инерции являются главные радиусы инерции се- чения, но они поменялись местами. Изобразим эллипс инерции для заданного сечения.

Об одном свойстве эллипса инерции. Провед¼м произвольную ось и касательную к эллипсу инерции, параллельную оси . Оказывается, что расстояние между касательной и осью есть радиус инерции отно-

сительно оси , тогда = 2 · .

При решении практических задач этим способом определения моментов инерции не пользуются, так как он приближ¼нный. Для этого нужно построить эллипс инерции и замерить . Однако эллипс инер- ции применяют для приближ¼нного контроля результатов определения главных центральных моментов инерции сечения и положения главных центральных осей. Покажем это на примере поперечного сечения в виде

-образного профиля.

1)Эллипс должен быть вытянут вдоль сечения (рис. 5.18).

Рис. 5.18. Направление эллипса инерции сечения

Почему это так? Потому, что одна из главных осей должна быть расположена вдоль сечения, только в этом случае = 0.

2) Эллипс инерции не может быть больше сечения. В одну сторону он может выйти за контур сечения, тогда в другую нет. Эллипс инерции также не может быть намного меньше сечения (рис. 5.19).

ГЛАВА 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНОГО СЕЧЕНИЯ БРУС

Рис. 5.19. Размеры эллипса инерции сечения

20 · . Следовательно 0 среднеквадратичная величина из ординат сечения, тогда 0 <| 0 |наиб, поэтому в обе стороны эллипс инерции не

может выходить за сечение. Радиус инерции 0 не может также быть значительно меньше среднеквадратичной величины 0.

5.9Определение моментов инерции сложных сечений

Довольно часто детали, испытывающие изгиб, имеют сложное поперечное сечение. Чтобы рассчитать брус на изгиб, нужно знать положение главных центральных осей и главные центральные моменты инерции се- чения.

Рассмотрим произвольное сечение, которое разбиваем на простые,

определяем площади и моменты инерции составных частей относительно

собственных центральных осей ( , , , ) (рис. 5.20).

Рис. 5.20. Определение моментов инерции сложных сечений

По формуле Вариньона определяем положение центра тяжести всего сечения относительно произвольных осей ,

ãäå , - координаты центров тяжести составных частей.

Далее проводим центральные оси , , их нужно направить параллельно выбранным осям для составных частей.