
Сопромат Лекции Часть 1
.pdf
ГЛАВА 7. КРУЧЕНИЕ |
120 |
Из верхнего треугольника: = · , из вертикального треугольника:= · , отсюда · = · , тогда
= · .
Эта формула выражает закономерности деформации при кручении. Теперь выразим эту закономерность в напряжениях, для этого нужно знать напряж¼нное состояние элемента.
Покажем ещ¼ раз элемент и напряжения, действующие по его граням, (они были рассмотрены при изучении темы "Сдвиг"). По четыр¼м граням элемента действуют только касательные напряжения это чистый сдвиг (рис. 7.8). Следовательно, при кручении вала круглого поперечного сечения в любой его точке реализуется чистый сдвиг.
Рис. 7.8. Напряж¼нное состояние вала
При чистом сдвиге = · , поэтому
= · ·
это уравнение совместности деформаций в напряжениях.
Теперь составим уравнения равновесия (статики). Покажем попереч- ное сечение вала, крутящий момент к > 0. Покажем элементарную
часть сечения и напряжение , действующее в ней (рис. 7.9). Составим уравнение равновесия
∫
∑
= · = к.
Решая совместно уравнение совместности деформаций и уравнение равновесия, получим
· · ∫ 2 = к.

ГЛАВА 7. КРУЧЕНИЕ |
121 |
Рис. 7.9. Поперечное сечение вала
Величины и выносим за знак интеграла, так как они не зависят от
радиуса. В этой формуле интеграл представляет собой полярный момент |
|||
инерции поперечного сечения вала: = |
· 4 |
. Тогда |
|
32 |
|||
|
|
||
= = · к ,
где относительный угол закручивания, то есть угол закручивания
вала длиной, равной единице.
Чем больше полярный момент инерции, тем меньше относительный угол закручивания , то есть тем ж¼стче вал, поэтому произведение · называется ж¼сткостью вала при кручении.
Подставим |
|
в формулу (1), тогда = · · |
к |
. Сократив , |
|
|
|
|
|||
|
|
· |
|||
получим окончательную формулу для касательных напряжений при кру-
чении = к · .
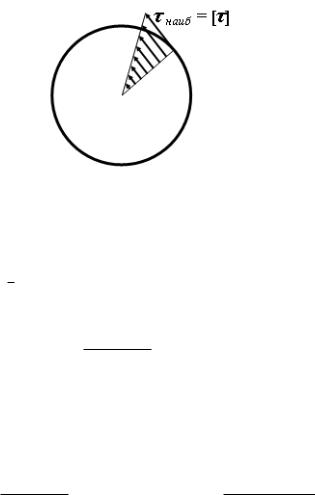
Изобразим эпюру касательных напряжений на любом радиусе (рис. 7.10).
Видно, что наибольшие касательные напряжения действуют на по-
|
к |
|
|
· наиб, íî |
|
|
||
верхности вала и равны наиб |
= |
|
|
|
|
= момент |
||
|
наиб |
|||||||
сопротивления вала кручению, тогда |
|
|
|
|
|
|
||
наиб = |
|
|
к |
, |
|
|
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
где для круглого сечения = |
· 3 |
. |
|
|
||||
|
16 |
|
|
|
|
|
|
|
Переходим к расч¼ту на прочность. Условие прочности при кручении по любой теории наиб ≤ [ ]. По IV теории, которая наболее точна для
ГЛАВА 7. КРУЧЕНИЕ |
122 |
Рис. 7.10. Распределение касательных напряжений
деталей из пластичных материалов, связь между допускаемыми напря-
[ ]
жениями: [ ] = √3.
Подставим в условие прочности значение наиб в наиболее опасном
сечении
| к | наиб ≤ [ ].
Это условие прочности при кручении для всего вала. Здесь | к | наиб áå-
р¼тся с эпюры крутящего момента. По этому условию проверяется проч- ность вала (первая задача).
Вторая задача назначение размеров поперечного сечения решает-
ñÿ òàê |
|
|
|
èëè ≥ √3 |
|
|
|
|
|
≥ |
| к | наиб |
, |
|
16· | к | наиб |
. |
||
|
[ ] |
[ ] |
||||||
|
|
|
|
|
· |
|
|
|
Третья задача определение грузоподъ¼мности
| к | наиб≤ [ ] · .
По этой формуле определяется наибольший крутящий момент, а зная | к | наиб, можно найти допускаемые внешние пары сил.
Несколько слов о наиболее экономичном сечении вала. Покажем эпюру напряжений в вале сплошного сечения. Здесь возможности материала полностью используется только на поверхности вала. Остальной материал недогружен, особенно у оси. Поэтому необходимо убрать материал от оси. Получим (рис. 7.11) пустотелый вал.
У пустотелого вала весь материал работает при напряжениях, близких к допускаемому. Применение пустотелого вала приводит к увели- чению его грузоподъ¼мности при той же площади поперечного сечения.

ГЛАВА 7. КРУЧЕНИЕ |
123 |
Рис. 7.11. Выбор наиболее экономичного сечения вала
Но, если стенка вала очень тонкая, то может быть местная потеря устой- чивости.
Покажем, что при кручении имеются сжимающие напряжения, которые могут привести к потере устойчивости тонкостеннго вала. В любой
точке вала (круглого) чистый сдвиг. Главные напряжения действуют на площадках, пов¼рнутых на угол 45 , и сжимающее главное напряже-
íèå 3 = − (ðèñ. 7.12).
Рис. 7.12. Сжимающие напряжения
Напомним формулу момента сопротивления кручению для пустоте- |
|||||||||
ëîãî âàëà |
|
= |
· 3 |
· |
(1 |
− |
4 |
). |
|
|
16 |
4 |
|||||||
|
|
|
|
||||||
7.3Перемещения при кручении круглого вала
Перемещения вала вполне определены, если известен угол поворота поперечного сечения вала, т.к. поперечные сечения вала поворачиваются как ж¼сткие диски.
Изобразим вал, нагруженный внешними парами сил (рис. 7.13). Будем рассматривать угол на участке . это угол, на который сечение поверн¼тся относи-
тельно сечения , где и произвольные сечения. Как определить ? В предыдущем параграфе было получено:
|
= |
|
к |
, |
|
= |
к |
· . |
|
|
|
|
|||||
|
· |
· |
||||||

ГЛАВА 7. КРУЧЕНИЕ |
124 |
Рис. 7.13. Перемещения вала
Здесь угол закручивания вала на элементарном участке . Чтобы получить угол закручивания вала на участке , просуммиру-
ем углы закручивания элементарных участков
= ∫ |
|
· · . |
|
|
|
к |
|
Это общая формула для определения угла закручивания вала на участке
.
Теперь определим угол закручивания всего вала
= ∫0 |
|
· |
· |
|
|
к |
|
угол, на который одно торцевое сечение поверн¼тся относительно другого.
Если крутящий момент на каждом участке постоянен и вал постоянного поперечного сечения, то
∑ ( ) · ( )
= к .·
Если, в частном случае по всей длине вала к = , òî
= к ··
угол закручивания вала при постоянном крутящем моменте.
Îзнаке. Угол закручивания вала может быть как положительным,
так и отрицательным. Из формулы видно, что знак совпадает со знаком крутящего момента.
ГЛАВА 7. КРУЧЕНИЕ |
125 |
1) Если при расч¼те по формулам получилось > 0, то это означает,
что одно сечение повернулось относительно второго сечения против хода часовой стрелки, если смотреть со стороны первого сечения.
2)Если < 0, то поворот происходит по часовой стрелке.
7.4Расчёт винтовых цилиндрических пружин с небольшим углом подъёма витка
Точный расч¼т на прочность винтовых пружин достаточно сложен, т.к. проволока винтовой пружины одновременно может испытывать растяжение (сжатие), кручение, сдвиг и изгиб.
Винтовая пружина может рассматриваться как пространственно изогнутый брус, ось которого представляет собой винтовую линию. Е¼ форма определяется средним диаметром витка , числом витков и углом
подъема . Подъ¼м витка можно характеризовать также шагом пружины . = · · tg . Для всех встречающихся на практике пружин шаг намного меньше длины окружности · , следовательно, угол подъ¼ма может рассматриваться как величина малая. Обычно < 5 .
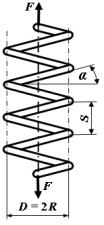
Пусть цилиндрическая винтовая пружина со средним диаметром витков , имеющая витков, угол подъема и диаметр поперечного
сечения проволоки, растягивается силами , приложенными вдоль оси пружины (рис. 7.14).
Рис. 7.14. Винтовая пружина
Используя метод сечений, рассмотрим равновесие верхней части пружины (рис. 7.15, а). Действие отброшенной части заменим поперечной

ГЛАВА 7. КРУЧЕНИЕ |
126 |
силой = и крутящим моментом к = · /2. В силу малости угла наклона витков нормальной силой и изгибающим моментом можно
пренебречь, тогда в поперечном сечении витка будут действовать толmко |
|||||||
две группы касательных напряжений: от среза = |
|
= |
4 · |
||||
|
· 2 (ðèñ. |
||||||
7.15, б) и от кручения = |
к |
= |
8 · · |
|
|
||
|
· 3 |
(ðèñ. 7.15, â) . |
|
||||
|
|
|
|||||
Рис. 7.15. Напряжения в поперечном сечении пружины
Как видно из распределения напряжений, в точке В поперечного се-
чения витка на внутренней стороне пружины касательные напряженияè совпадают по направлению, поэтому
|
|
= + |
= |
4 · |
+ |
8 · · |
= |
4 · · |
· |
(1 + |
2 · |
) |
|
|
|
· 2 |
|
· 3 |
|
· 2 |
|
|
|||
.
На внутренней и наружной поверхностz[ витка радиусы кривизны различны, поэтому используют более точную формулу для наибольших касательных напряжений
|
|
= |
8 · · |
· |
( |
4 |
· − 1 |
+ |
0, 615 |
), ãäå = / . |
|
· 3 |
4 |
· − 4 |
|
||||||
|
|
|
|
|
||||||
Для пружин большого диаметра из тонкой проволоки / >> 1,
поэтому касательные напряжения от кручения значительно больше напряжений от среза , которые можно не учитывать, тогда
= |
8 · · |
. |
|
· 3 |
|
При таком упрощении легко вычислить перемещение оси пружины (осадку), которая обозначается через . Вырежем из пружины элемент
длиной (рис. 7.16). После нагружения второе сечение поворачивается

ГЛАВА 7. КРУЧЕНИЕ |
127 |
Рис. 7.16. Перемещения в цилиндрической пружине
отностительно первого на угол , где = к· , тогда = · =
·
к·· · .
Просуммируем осадку по всей длине стержня пружины
|
= ∫0 |
|
·· |
|
∫0 |
|
||
|
= · |
= · · · , |
||||||
|
|
|
к |
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
ãäå = ∫ |
полная длина стержня пружины. Пренебрегая наклоном |
|||||||
0
витков к горизонтали получим = 2 · · · , где количество витков.
· 4
Ó÷ò¼ì, ÷òî к = · , = 2 .
Подставив полученные соотношения в выражение для , получим
= |
· |
|
· · 2 · · · · 2 |
= |
4 3 |
= |
8 3 |
. |
|
· · 4 |
4 |
|
|
||||||
|
|
|
|
4 |
|||||
Теперь об условии ж¼сткости пружины: ≤ [ ], где [ ] допускаемое значение осадки, следовательно
8 3
4
≤ [ ]
условии ж¼сткости пружины.
7.5Кручение брусьев некруглого сечения
При кручении брусьев некруглого поперечного сечения гипотеза плоских сечений не применима, так как при закручивании происходит депланация (искривление) сечения. В связи с этим методами сопротивления материалов напряжения определить невозможно. Методами теории

ГЛАВА 7. КРУЧЕНИЕ |
128 |
упругости для брусьев прямоугольного сечения получены следующие зависимости (рис. 7.18).
Рис. 7.17. Кручение прямоугольного бруса
max = |
к |
, |
= |
к · |
, |
′ |
= |
· |
max, |
||
к |
|
||||||||||
|
|
|
|
· |
к |
|
max |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
ãäå max напряжение, действующее на поверхности бруса посередине большей стороны прямоугольника;
max′ напряжение, действующее на поверхности бруса посередине меньшей стороны прямоугольника;
к = · · 2 геометрический фактор прочности (условный момент
сопротивления сечения кручению);к = · · 3 геометрический фактор ж¼сткости (условный момент
инерции сечения при кручении).
Значения коэффициентов , , в зависимости от соотношения размеров прямоугольника / приведены в таблице
a/b |
1 |
1,5 |
2 |
3 |
4 |
6 |
8 |
10 |
∞ |
|
0,208 |
0,213 |
0,246 |
0,285 |
0,282 |
0,299 |
0,307 |
0,313 |
0,333 |
|
|
|
|
|
|
|
|
|
|
|
0,141 |
0,196 |
0,229 |
0,263 |
0,281 |
0,299 |
0,307 |
0,313 |
0,333 |
|
|
|
|
|
|
|
|
|
|
|
1,000 |
0,859 |
0,795 |
0,753 |
0,745 |
0,743 |
0,742 |
0,742 |
0,742 |
|
|
|
|
|
|
|
|
|
|
7.6Кручение тонкостенных брусьев (свободное кручение)
Кручение брусьев некруглого сечения может быть свободным или стесн¼нным. При свободном кручении нет препятствий к искривлению поперечных сечений. Брус будет испытывать свободное кручение, если

ГЛАВА 7. КРУЧЕНИЕ |
129 |
по его длине крутящий момент и размеры поперечного сечения не меняются, а также нет защемления.
Характерной особенностью тонкостенных брусьев является то, что толщина ( ) значительно меньше длины ( ) контура сечения ( > 10· ).
Тонкостенные брусья разделяются на брусья с замкнутым и открытым профилем. У брусьев с открытым профилем средняя линия поперечного сечения является незамкнутой кривой(рис. 7.18).
Рис. 7.18. Тонкостенные брусья открытого профиля
У брусьев с замкнутым профилем средняя линия поперечного сече- ния замкнутая кривая (рис. 7.19).
Рис. 7.19. Тонкостенные брусья с замкнутым профилем
7.6.1Свободное кручение тонкостенных брусьев с открытым профилем
Напряжения в брусьях с открытым профилем сильно не изменятся, если его распрямить. Тогда можно использовать расч¼тные формулы для прямоугольного сечения с большим соотношением сторон ( > 10· ), для
которых = = 1/3 (рис. 7.20)
к = |
1 |
· · 2, |
к = |
1 |
· · 3 |
|
|
|
|
||||
3 |
3 |
|||||
,
