
Сопромат Лекции Часть 1
.pdf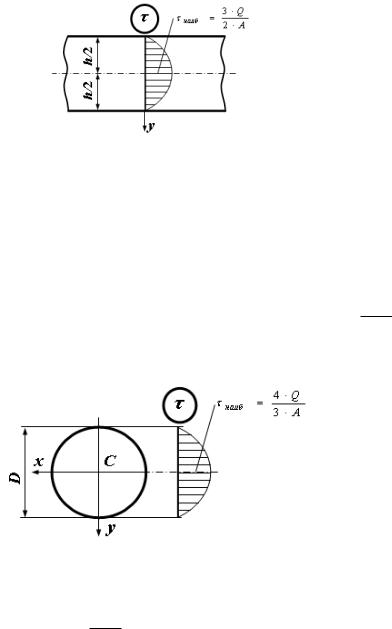
ГЛАВА 6. ИЗГИБ |
100 |
Рис. 6.29. Распределение касательных напряжений по высоте прямоугольного сечения
можно установить и без формулы, по закону парности касательных напряжений, так как внешние поверхности не нагружены.
Необходимо обратить внимание на то, что касательные напряжения
по высоте распределены неравномерно. Наибольшие касательные напря-
3 ·
жения действуют в точках на нейтральной оси и равны наиб = 2 · .
2. Касательные напряжения в балке круглого поперечного сечения (без вывода) (рис. 6.30).
Рис. 6.30. Распределение касательных напряжений по высоте круглого сечения
4 ·
В этом случае наиб = 3 · это меньше, чем в прямоугольном се- чении.
3. Касательные напряжения в балке двутаврового сечения (рис. 6.31). Построим эпюру касательных напряжений по высоте сечения без чи- сел, рассуждая по формуле Журавского. Пусть точка, в которой определяется , перемещается от верхних волокон к нижним. В пределах полки
быстро возрастает статический момент отс и практически не меняется ширина сечения ( ). По высоте стенки медленно возрастает (до ней-
тральной оси) отс и не меняется ( ), а на границе полки со стенкой

ГЛАВА 6. ИЗГИБ |
101 |
Рис. 6.31. Распределение касательных напряжений по высоте двутавра
резко уменьшается ( ) (на эпюре скачок). Ниже нейтральной оси
эпюра симметрична с верхней частью. Наибольшие касательные напряжения и в этом случае действуют в точках на нейтральной оси.
Выводы: 1. Наибольшие касательные напряжения для симметричных сечений действуют в точках на нейтральной оси.
2. Вид эпюры касательных напряжений существенно зависит от формы поперечного сечения, в то время как вид эпюры нормальных напряжений не зависят от формы сечения.
6.8Расчёт балок на прочность по допускаемым напряжениям
При расч¼те балок по допускаемым напряжениям за опасное принимается такое состояние при котором эквивалентные напряжения достигают предела текучести т. Этот способ расч¼та применяется для балок, в
которых остаточные деформации недопустимы. Выбираем в произвольном сечении балки (рис. 6.32) произвольную точку , в которой будем
оценивать прочность (в дальнейшем будем оценивать прочность в опасном сечении). В поперечном сечении действуют поперечная сила и
изгибающий момент пусть для определ¼нности они будут положи-
тельными. |
|
|
|
|
· отс |
|
||||
По формулам = |
· |
, |
= |
определяем напряжения и |
||||||
|
|
|
||||||||
строим их эпюры. |
|
|
|
|
· |
( ) |
|
|||
|
|
|
|
|
|
|||||
Теперь, в окрестности точки вырежем элемент и покажем напряже-
ния по граням (рис. 6.33). На верхней и нижней площадках нормальных напряжений нет, действуют только касательные напряжения. На боковых гранях действуют и нормальные, и касательные напряжения. Эле-
мент испытывает плоское напряж¼нное состояние: = , |
= , |
|
= 0, |
= − . |
|

ГЛАВА 6. ИЗГИБ |
102 |
Рис. 6.32. Расч¼т на прочность в произвольной точке
Рис. 6.33. Напряж¼нное состояние детали в точке
Для составления условия прочности необходимо найти главные напряжения
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
· [( + ) ± √( − )2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
, = |
+ 4 · 2 |
] = |
· ( ± √ 2 + 4 · 2). |
|||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
2 |
2 |
|||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
√ |
|
|
|
|
|
1 |
|
|
|
|
√ |
|
|
|
|
|
|||||
Тогда |
|
= |
· ( + |
|
2 |
2 |
), |
= |
· ( − |
|
2 |
2 |
). |
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
2 |
2 |
|
|||||||||||||||||||||||||
|
|
|
+ 4 · |
|
|
+ 4 · |
|
|||||||||||||||||||||
|
Так как ≥ 0 и ≤ 0, присвоим главныем напряжениям араб- |
||||||||||||||||
|
|
|
|
|
1 |
|
√ |
|
|
|
|
|
|
1 |
|
||
ские индексы |
1 |
= |
· ( + |
|
2 |
2 |
), |
2 = 0, |
3 = |
· ( − |
|||||||
|
|
|
|||||||||||||||
2 |
2 |
||||||||||||||||
√ |
|
). |
|
|
+ 4 · |
||||||||||||
2 + 4 · 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Далее следует воспользоваться подходящей теорией прочности. Балки обычно изготавливаются из сталей, из алюминиевых или магниевых сплавов, то есть из пластичных материалов, поэтому воспользуемся IV-й теорией прочности.
√
экв ≤ [ ], экв = 12 + 22 + 32 − 1 · 2 − 2 · 3 − 3 · 1.
√
Подставив значения главных напряжений, получим экв = 2 + 3 · 2. Эта формула применима не только для положительных и , но и для

ГЛАВА 6. ИЗГИБ |
103 |
||
|
√ |
|
≤ [ ] условие прочности для произ- |
отрицательных. Тогда |
2 + 3 · 2 |
||
вольной точки балки по способу допускаемых напряжений.
Чтобы проверить прочность всей балки, нужно взять опасную точку
наиболее опасного сечения, т. е. для всей балки наиб |
≤ [ ]. |
|||
|
|
|
экв |
|
Как найти наиб |
экв |
|
= ( , ) на экстремум. |
|
экв ? Нужно исследовать |
|
|
|
|
Сначала исследовать по контуру сечения, затем внутри, найти все экстремумы, а затем выбрать наибольшее по абсолютной величине значе- ние.
Опыт расч¼тов, накопленных к настоящему времени, показывает, что наибольшие эквивалентные напряжения могут быть в одной из следующих точек:
1.точка с наибольшим по абсолютной величине нормальным напряжением;
2.точка с наибольшим касательным напряжением в поперечном се- чении;
3.точка в месте резкого изменения ширины поперечного сечения в сечении с большими значениями поперечных сил и изгибающих моментов.
Рассмотрим подробнее эти точки.
Первая опасная точка (почти всегда она и бывает самой опасной)(рис. 6.34).
Рис. 6.34. Первая опасная точка
Наибольшие по абсолютной величине нормальные напряжения возникают в наиболее удал¼нной от нейтральной оси точке сечения, где
действует |
| |
|
| |
наиб, и равны |
| |
|
| |
наиб= |
|
| |наиб |
· | |
|
| |
наиб . |
|
|||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Будем применять условие прочности: | |=| |наиб, |
= 0, тогда |
|||||||||||||||||
экв =| |наиб ≤ [ ]. |
|
|
|
|
|
= , тогда условие прочности в |
||||||||||||
|
|
|
наиб |
|
||||||||||||||
наиб |
|
|
|
|
Íî |
|
| |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

ГЛАВА 6. ИЗГИБ |
104 |
первой опасной точке запишется в виде
| |наиб
≤ [ ].
Таким образом, первая опасная точка находится в сечении с наибольшим по абсолютной величине изгибающим моментом в наиболее удал¼нной от нейтральной оси точке.
Вторая опасная точка (ðèñ. 6.35).
Рис. 6.35. Вторая опасная точка
Это точка с наибольшими касательными напряжениями. Выясним, где она находится. По формуле Журавского
= |
· отс |
, |
тогда |
наиб = |
| |наиб |
( |
отс |
)наиб. |
|||
|
|
|
|||||||||
|
|
· |
( ) |
|
|
|
|
|
· ( ) |
||
|
|
|
|
|
|
||||||
Наибольшее значение касательных напряжений будет тогда, когда выражение в круглой скобке будет наибольшим, то есть на нейтральной оси (н.о.).
наиб = | |наиб · ( отс )н.о..
( )
Таким образом, вторая опасная точка находится на нейтральной оси в сечении с наибольшей по абсолютной величине поперечной силой. За-
пишем условие прочности для этой точки. Для не¼: |
= 0, |
= наиб, |
|||||||||||||||||||||
|
|
|
|
√ |
|
|
|
|
|
√ |
|
|
|
|
|
|
|
[ ] |
|
|
|
||
тогда |
экв |
|
|
|
2 |
|
|
2 |
|
|
|
наиб. Íî |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
= |
|
|
+ 3 · |
|
= |
3 · |
|
|
|
[ ] = √3 |
. Следовательно, |
|||||||||
|
|
|
|
|
|
|
|
| |наиб |
· |
( |
отс |
)н.о. |
≤ |
[ ] |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
||||||||
условие прочности во второй опасной точке.

ГЛАВА 6. ИЗГИБ |
105 |
Рис. 6.36. Третья опасная точка
Эта точка бывает наиболее опасной только для коротких балок. Третья опасная точка (ðèñ. 6.36).
Эта точка находится в месте резкого изменения ширины сечения. Такое наблюдается, например, у двутавровых балок
√
экв = оп2 + 3 · оп2 ≤ [ ]
условие прочности в третьей опасной точке.
Эту точку нужно рассматривать в том сечении, где подкоренное выражение будет наибольшим. В ряде случаев это просто, когда | | наиб
и | | наиб находятся в одном сечении, тогда именно в этом сечении следует проверять третью опасную точку. Но, обычно | | наиб и | | наиб
находятся в разных сечениях, поэтому,учитывая, что в длинных балках главную роль играют нормальные напряжения, эту проверку (то есть проверку третьей опасной точки) делают в сечении с наибольшим изгибающим моментом.
Эта точка оказывается наиболее опасной весьма редко.
6.9Рациональная форма поперечного сечения балки
Рассмотрим два случая:
Первый случай, когда материал балки одинаково сопротивляется растяжению и сжатию.
В отыскании наиболее рациональной формы сечения будем отправляться от прямоугольного сечения. Касательные напряжения малы и здесь их учитывать не будем (рис. 6.37).

ГЛАВА 6. ИЗГИБ |
106 |
Рис. 6.37. Рациональная форма поперечного сечения балки
Из эпюры нормальных напряжений видно, что полностью возможности материала балки используются только в наиболее удал¼нных от нейтральной оси точках сечения, то есть в верхней и нижней точках. В других точках сечения возможности материала недоиспользуются, особенно сильно в области нейтральной оси. Необходимо перераспределить материал в область наибольших напряжений, тогда грузоподъ¼мность балки увеличится (за сч¼т увеличения и, соответственно, ). Îä- нако очень высокие балки применять нельзя, т. к. может быть потеря устойчивости.
Итак, наиболее экономичной формой поперечного сечения для балок, изготовленных из материала, одинаково сопротивляющегося и растяжению, и сжатию, является двутавр. Изгибающий момент большей частью воспринимается полками, так как значительные нормальные усилия приходятся на полки, а поперечная сила воспринимается стенкой.
Второй случай, когда материал балки неодинаково сопротивляется растяжению и сжатию, то есть [ ]сж > [ ]р.
Какая форма поперечного сечения наиболее экономична в этом слу- чае? Очевидно, наиболее экономичная форма такая, при которой напряжения в крайних волокнах будут равны допускаемым напряжениям. Построим вначале эпюру нормальных напряжений (рис. 6.38).
Далее, по эпюре построим сечение, для которого эта эпюра будет справедлива. Сечение должно иметь такую форму, чтобы его центр тяжести был смещ¼н по оси . Этого можно достичь, применяя тавровое
сечение, но, при этом необходимо, чтобы полка тавра испытывала растяжение. Применимы и двутавры, но разнополые, однако они сложнее в изготовлении.

ГЛАВА 6. ИЗГИБ |
107 |
Рис. 6.38. Рационалная форма поперечного сечения балки для случая, когда [ ]с > [ ]р
6.10Перемещения балок при изгибе
6.10.1Прогиб и поворот поперечного сечения балки
Рассмотрим консольную балку, нагруженную сосредоточенной силой. Ось направим вверх, т. к. необходимо получить основные формулы со
знаком "плюс"(рис. 6.39).
Рис. 6.39. Перемещения в балке
Строго говоря, силу нужно приложить к изогнутой балке.
Горизонтальные перемещения намного меньше вертикальных, поэтому их не рассматриваем. Перемещения балки:
прогиб балки в рассматриваемом сечении это вертикальное пере-
мещение центра тяжести поперечного сечения; после изгиба поперечное сечение оста¼тся плоским и перпендикулярным оси балки;
угол поворота поперечного сечения балки или поворот попереч-
ного сечения.
Зная и , можно определить положение любой точки балки. Пусть( ) уравнение изогнутой оси балки или уравнение упругой линии бал-

ГЛАВА 6. ИЗГИБ |
108 |
ки. Покажем угол ( ), на который поверн¼тся данное сечение балки. Да-
лее угол, образованный касательной к изогнутой оси и горизонталью, тоже равен углу ( ) (рис. 6.40). Следовательно, = tg , но tg ≈ ,
так как угол весьма мал. Деформации балки весьма малы даже при напряжениях, равных допускаемым, поэтому
Рис. 6.40. Связь между углом поворота и производной
= .
Правило знаков для : если > 0, тогда > 0 (случай, показанный на рисунке 6.40), то сечение поворачивается против часовой стрелки. А если
< 0, то по ходу часовой стрелки. Это правило справедливо для слу- чая, когда ось направлена слева направо. Если изменить направление оси , то изменится и правило знаков на противоположное.
Правило знаков для прогибов: если > 0, то прогиб происходит вверх, а если < 0, то прогиб происходит вниз. Знак прогиба не зависит от направления оси .
6.10.2Дифференциальное уравнение изогнутой оси балки
Запишем формулу для кривизны балки, которая была получена при выводе формулы для нормальных напряжений
1 = · . (1)
Эта формула получена для чистого изгиба, когда отсутствует попереч- ная сила. Что может изменить ? Она несколько изменяет прогибы и,

ГЛАВА 6. ИЗГИБ |
109 |
следовательно, кривизну, но поправка, которую вносит поперечная сила, невелика и ею пренебрегают. Поэтому формулу (1) можно применять и при поперечном изгибе. Она является практически точной (теоретически нет).
Рассмотрим любое сечение балки и элемент длиной . Из алгебры известно, что элемент можно считать элементом окружности.центр кривизны изогнутой оси балки в сечении . С помощью фор-
мулы (1) кривизна выражается через внешние силы, упругие свойства материала, размеры и форму поперечного сечения балки (рис. 6.41).
Рис. 6.41. Перемещения в консольной балке
Кривизну можно выразить и через уравнение изогнутой оси балки. Из алгебры известно
1 |
|
|
′′ |
|
|
|
|
= |
|
. |
(2) |
|
[1 + ( ′)2]23 |
||||
Чтобы приравнять правые части формул (1) и (2),необходимо выяс-
нить, будут ли они с одинаковым знаком.
Формула (1): балка изгибается выпуклостью вниз, поэтому 1 > 0, òàê как > 0; формула (2): 1 > 0, òàê êàê ′′ > 0, то есть эти формулы дают кривизну с одинаковым знаком. Теперь можно приравнять правые
части формул |
′′ |
|
|
|
= |
||
|
|
|
|
|
[1 + ( ′)2]23 |
· |
полное дифференциальное уравнение изогнутой оси балки. Здесь исключ¼н индекс у , т. к. в дальнейшем будем считать, что это момент
инерции сечения относительно нейтральной оси, а индекс писать не будем.
