Сопромат Лекции Часть 1

ГЛАВА 4. ТЕОРИЯ НАПРЯЖЁННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ 40

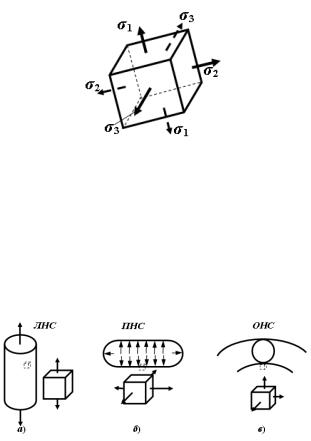
сделать, если известны напряжения на тр¼х взаимно перпендикулярных площадках. Следовательно, напряж¼нное состояние детали в точке зада¼тся напряжениями на тр¼х взаимно перпендикулярных площадках.

Выберем правую винтовую систему координат и в окрестности точкивырежем бесконечно малый элемент, грани которого перпендикулярны

координатным осям и покажем его отдельно (рис. 4.1, б).

Покажем напряжения на гранях элемента: , , нормальные напряжения ( , ‖ ); , , , , , - касательные напря- жения ( касательное напряжение на площадке, перпендикулярной оси и направленное параллельно оси ).

Элемент должен находиться в равновесии, поэтому напряжения на противоположных гранях должны быть такими же по величине и противоположными по направлению. Таким образом, на тр¼х взаимно перпендикулярных площадках действуют 9 напряжений или 9 компонент напряж¼нного состояния детали в точке. Выпишем их в виде тензора напряжений

.

По закону парности касательных напряжений: = , = ,= , то есть из 9 компонент останется только 6: , , , , ,

.

Зная эти 6 напряжений, можно определить напряжения на любой площадке, проходящей через данную точку .

Если площадку поворачивать, то напряжения на ней меняются, и всегда можно найти такое положение площадки, когда касательные напряжения на ней равны нулю.

Площадки, на которых касательные напряжения равны нулю, называются главными, а напряжения, действующие на этих площадках, называются главными напряжениями.

В теории упругости доказывается, что при любом напряж¼нном состоянии имеется как минимум три главных взаимно перпендикулярных площадки.

Покажем бесконечно малый элемент, грани которого параллельны главным площадкам (рис. 4.2). В этом случае (если известны главные напряжения и положение главных площадок), напряжения на любой площадке можно определить, имея три главных напряжения 1, 2, 3, ïðè- ÷¼ì 1 ≥ 2 ≥ 3, òî åñòü 1 алгебраически наибольшее напряжение ( 1 = наиб), à 3 алгебраически наименьшее напряжение ( 3 = наим).

ГЛАВА 4. ТЕОРИЯ НАПРЯЖЁННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ 41

Рис. 4.2. Главные напряжения

Какие бы площадки, проходящие через данную точку . мы не рас-

сматривали, напряжения на них не могут быть больше 1 и меньше 3. В частных случаях некоторые из главных напряжений могут быть равными нулю. В связи с этим различают 3 вида напряж¼нных состоя-

íèé:

Рис. 4.3. Виды напряж¼нных состояний

I. Линейное напряж¼нное состояние (ЛНС) (рис. 4.3, а):

1)1 ̸= 0, 2 = 3 = 0 центральное растяжение;

2)1 = 2 = 0, 3 ̸= 0 центральное сжатие.

II. Плоское напряж¼нное состояние (ПНС) (рис. 4.3, б):

1)1 ̸= 0, 2 ̸= 0, 3 = 0;

2)1 ̸= 0, 2 = 0, 3 ̸= 0;

3)1 = 0, 2 ̸= 0, 3 ̸= 0.

III. Объ¼мное напряж¼нное состояние (ОНС) (рис. 4.3, в):

1 ̸= 0, 2 ̸= 0, 3 ̸= 0.

ГЛАВА 4. ТЕОРИЯ НАПРЯЖЁННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ 42

4.2Напряжения на произвольной площадке при линейном напряжённом состоянии

Рассмотрим деталь произвольной формы ( рис. 4.4, а). Пусть хотя бы в одной точке этой детали реализуется линейное напряж¼нное состо-

яние. В окрестности этой точки вырежем бесконечно малый элемент и покажем его отдельно.

Рис. 4.4. Линейное напряж¼нное состояние

Пример такого нагружения брус при центральном растяжении или сжатии (рис. 4.4, б). Покажем, что при центральном растяжении действует лишь одно из главных напряжений. Вырежем в окрестности точки элемент, верхняя и нижняя грани которого перпендикулярны оси бруса. На этих гранях действует только нормальное напряжение, касательных напряжений нет. На боковых гранях нет ни нормальных, ни касательных напряжений (слои друг на друга не давят), то есть имеет место линейное напряж¼нное состояние.

Рассмотрим произвольную площадку, проходящую через данную точ- ку . Положение этой площадки (рис. 4.4, в) определяется нормалью , то есть углом ( ). Рассмотрим действие верхней части элемента на нижнюю. Вв¼дем следующее правило знаков для угла : при повороте

против хода часовой стрелки угол положительный, а при повороте по ходу часовой стрелки отрицательный. Если обозначить через пло-

щадь нижней грани элемента, то площадь наклонной площадки будет равна / .

Покажем нормальное и касательное напряжения, действующие на площадке , и выразим их через . Направим ось по направлению

, à îñü и составим уравнения равновесия для нижней части элемента

ГЛАВА 4. ТЕОРИЯ НАПРЯЖЁННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ 43

Таким образом, мы получили формулы для определения напряжений на произвольной площадке при линейном напряж¼нном состоянии.

Проанализируем полученные формулы.

Формула для нормальных напряжений: =| | _наиб = при2 = 1 èëè ïðè = ±1; = ± , ãäå = 0, ±1, ±2, . . . , òî

есть при любых попадаем на те же главные площадки. Следовательно,

Следовательно, какое бы не брали, всегда будем попадать на одну из площадок, наклон¼нных к главным площадкам под углом 45 (ðèñ. 4.5). Строго говоря, | | наиб действуют по конической поверхности.

Рис. 4.5. Наибольшие касательные напряжения

4.3Напряжения на произвольной площадке при плоском напряжённом состоянии

Рассмотрим произвольно нагруженное тело (рис. 4.6,а). Выберем точ- ку , в которой имеет место плоское напряж¼нное состояние, то есть элемент в этой точке нагружен лишь по двум граням. Вырежем в окрестности точки элемент, грани которого параллельны главным площадкам, и покажем его отдельно (рис. 4.6, б).

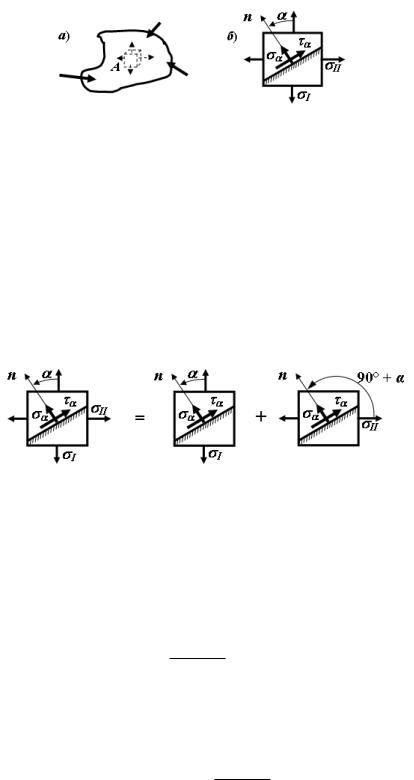
ГЛАВА 4. ТЕОРИЯ НАПРЯЖЁННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ 44

Рис. 4.6. Напряжения на произвольных площадках

Изобразим произвольную площадку и напряжения и íà íåé, которые нам необходимо определить. Обозначим через угол между

наибольшим из главных напряжений и нормалью к площадке, тогда угол между напряжением и нормалью будет равен + 90 .

В сопротивлении материалов рассматриваются линейные системы, поэтому напряжения (деформации, перемещения) от группы сил можно найти как сумму напряжений (деформаций, перемещений) от каждой силы в отдельности (рис. 4.7). Этот принцип называется принципом независимости действия сил или принципом суперпозиции.

Рис. 4.7. Суммирование напряжений

Следовательно, = + ,

Таким образом, мы получили формулы преобразования напряжений при повороте от главных площадок при плоском напряж¼нном состоянии.

Проанализуем полученные формулы

| |наиб= − ,

2

ГЛАВА 4. ТЕОРИЯ НАПРЯЖЁННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ 45

при sin 2 = ±1, откуда = ±4 + 2 .

Следовательно, наибольшие касательные напряжения равны полусумме главных напряжений и действуют на площадках, равнонаклон¼нных к главным (рис. 4.8).

Рис. 4.8. Положение площадок с наибольшими касательными напряжениями

4.4Графический способ определения напряжений при плоском напряжённом состоянии. Круги Мора

Âпредыдущем параграфе были получены формулы для определения напряжений на произвольной площадке при плоском напряж¼нном состоянии

Если в этих формулах исключить , то получим зависимость = ( ), которая в осях , отображает окружность с центром на оси . О.Х. Мор

использовал это обстоятельство для определения напряжений графиче- ским способом. При этом можно решить два вида задач.

I задача (прямая)

Дано: , , (рис. 4.9). Требуется определить: , .

Изложим последовательность операций, а затем докажем, что они правомерны (рис. 4.10).

Провед¼м оси , и отложим отрезки, равные главным напряжениям = , = . На отрезке , как на диаметре, построим окружность с центром в точке . Полученная окружность называется кругом Мора или кругом напряжений. Пров¼дем из центра окружности

ГЛАВА 4. ТЕОРИЯ НАПРЯЖЁННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ 46

Рис. 4.9. Определение напряжений на произвольной площадке

Рис. 4.10. Графическое определение напряжений на произвольной площадке

радиус под углом 2 от оси против хода часовой стрелки (так как считаем, что угол положительный) и докажем, что координаты полу- ченной точки соответствуют напряжениям на площадке .

òî åñòü = .

Итак, мы доказали, что с помощью круга Мора можно определить напряжения на произвольной площадке . Следовательно, задача реше-

íà.

Точку можно было найти также с помощью хорды, провед¼нной из точки под углом к оси .

Графический способ Мора менее точный, чем аналитический. Однако, графическая интерпретация плоского напряж¼нного состояния детали в точке является весьма удобной для анализа. Видно, что: = наиб,

ГЛАВА 4. ТЕОРИЯ НАПРЯЖЁННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ 47

жения действуют на площадках, равнонаклон¼нных к главным площадкам.

Теперь найд¼м на круге Мора точку, соответствующую площадке , перпендикулярной площадке , т.е. = + 90 . Провед¼м радиус под углом 2 = 2 + 180 и получим точку ( , = − ).

Важный вывод: точки, соответствующие двум взаимно перпендикулярным площадкам, лежат на концах одного диаметра круга Мора.

II задача (обратная).

Дано: , , , . Требуется определить: , , 0( ).

Рис. 4.11. Главные площадки и главные напряжения

Эта задача имеет для практики более важное значение, чем прямая задача.

Проводим координатные оси (рис. 4.12) , и строим в этих осях

точки ( , ) ( , ). Так как эти точки соответствуют взаимно перпендикулярным площадкам, то они лежат на концах одного диаметра круга Мора. Соединяем эти точки и определяем положение центра круга. Имея центр и диаметр, можно провести единственную окружность.

Задача решена.

= , = .

Провед¼м хорду и получим угол от до , а нам нужен угол

ГЛАВА 4. ТЕОРИЯ НАПРЯЖЁННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ 49

Изобразим элемент отдельно (рис. 4.14). Покажем произвольную площадку, проходящую через точку . Нормаль к площадке образует с

главными напряжениями углы 1, 2, 3. Покажем напряжения на этой площадке , .

Рис. 4.14. Определение напряжений на произвольных площадках при объ¼мном напряж¼нном состоянии

Задача сводится к следующей: известны 1, 2, 3, 1, 2, 3. Требуется определить: , .

Воспользуемся принципом суперпозиции, то есть представим напряжения на произвольной площадке как сумму напряжений от каждого главного напряжения в отдельности

Касательные напряжения, вызванные каждым главным напряжением, по направлению не совпадают, поэтому необходимо рассматривать векторную сумму

Для определения направления в каждом случае необходимо рассматривать конкретную задачу.

Пример: определим напряжения на октаэдрической площадке, то есть на площадке, равнонаклон¼нной к главным 1 = 2 = 3 = окт

Из линейной алгебры известно, что cos2 1 + cos2 2 + cos2 3 = 1,