2.3 Зависимость между моментами инерции относительно

x₁

параллельных осей, одни их которых центральные

Для произвольного сечения, представленного на рис. 2.6, проведем центральные осиx,y, относительно которыхS_х = Sу = 0, а затем параллельные им оси Х₁, У₁. Координаты центра тяжести в этих осях обозначим черези b, тогда координаты элементарной площадки dA будут х₁=,у₁=.

Рассмотрим осевой момент инерции относительно оси Х₁:

Рис.2.6

= ++ dA.

Так как dA=S_х= 0, dA=, dA = А , то= + А,

Аналогично ═+А.

Таким образом, осевые моменты инерции относительно произвольных осей, параллельных центральным, находятся как сумма моментов инерции относительно центральных осей и произведения площади сечения на квадрат расстояния между осями, центробежный момент инерции – как сумма центробежного момента инерции относительно центральных осей и произведения площади сечения на расстояния между осями.

2.4 Главные оси и главные моменты инерции сечения

Рассмотрим некоторое сечение в координатной системе x,y, а затем в координатной системеx₁,y₁, поверну-той относительно исходной на 90⁰(рис.2.7). Из рисунка следует:

х₁ = у, у₁ = - х. Тогда=х₁у₁dA ═ -хуdA ═ -І_{ху .}

Таким образом, при повороте осей на 90 ⁰центробежный момент инерции меняет знак, следовательно, есть такое положение осей, в которых центробежный момент инерции равен нулю. Такие оси называются главными. Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями инерции сечения.

М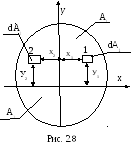оменты инерции относительно главных центральных осей называются главными центральными моментами инерции и обозначаются,, причем>.

Если сечение имеет ось симметрии (ось yна рис.2.8), то эта ось всегда будет главной осью инерции сечения. Действительно, для любой элементарной площадки в окрестности точки 1 в силу симметрии найдется такая же площадка в окрестности точки 2. При этом А₁=А_2,у₁=у₂, х₁= -х_2,, тогда=+.

Таким образом, ось у является главной осью, так как центробежный момент инерции относительно её равен нулю.

2.5 Зависимость между моментами инерции при повороте осей

Пусть задана система координат главных центральных осейx₀,y_0, для которой известны моменты инерции, центробежный момент инерции в этих осях равен нулю (рис.2.9). Вычислим моменты инерции этого сечения относительно новых осейx,y, повернутых по отношению к главным на угол α - угол между осями x₀иx. Он будет положительным, если поворот от осиx₀к оси x происходит против часовой стрелки и отрицательным - если по часовой стрелке.

Из рис. 2.9 следует:

=,

y=

С учетом этих формул запишем выражения для моментов инерции рассматриваемого сечения в координатных осях x,y:

I_х ==(у₀ cоsα - х₀sinα)² dA =уcоs²αdA­–

-2х ₀у₀cоsα·sinα dA+sin²α dA,

т.е. = cоs²α - 2 Іх ₀у₀ cоsα· sinα + sin²α.

І_у==(х₀csα + у₀sinα)² dA =хcоs²α dA+­­­­­+2х ₀у₀cоsα·sinα dA+уsinαdA=

= cоs²α + 2 Іх ₀у₀ cоsα ·sinα +sin²α.

І_ху= = =

==

= cos²α·cоsα ·sinα +cоsα∙sinα -sin²α.

Так как , cоsα ∙sinα =, то окончательно получим

.

Складывая выражения І_х и І_у, получим

.

Таким образом, при повороте координатных осей сумма осевых моментов инерции не изменяется.