6.6.2 Напряжения при поперечном изгибе

При поперечном изгибе в сечении бруса кроме изгибающего момента действует и поперечная сила. Следовательно, в этом случае в поперечных сечениях бруса возникают не только нормальные, но и касательные напряжения.

Теоретические и экспериментальные исследования показывают, что формула нормальных напряжений при чистом изгибе применима и для поперечного изгиба, если отношение длины балки к её высоте ℓ/h>5.

Вырежем часть балки, испытывающей пря-мой поперечный изгиб, длинной dz двумя плоскостями, перпендикулярными её оси и плоскостью, параллельной оси на расстоя-нии у от неё (рис.6.20). По торцам этого эле-мента будут действовать нормальные напря-жения σ и касательные напряжения τ, свя-занные с поперечной силой зависимостью .

В элементарной теории изгиба принимается, что касательные напряжения по ширине се-чения b(y)остаются постоянными, изменяя-ются лишь по высоте. В плоскости сечения,

Рис.6.20

параллельной оси балки, также будут действовать касательные напряжения согласно закону парности касательных напряжений.

Составим уравнение равновесия рассматриваемого элемента, спроектировав все силы на ось балки Z :

- N - dT + N + dN = 0 или dT = dN,

здесь , N=.

С учётом формулывыражение нормальной силы примет вид:N=,

где , тогдаN=, dN==, откуда следует.

Так как , то окончательно получим

. (6.13)

Выведенная формула впервые была получена Д.И.Журавским и носит его имя, из неё следует, что знак касательных напряжений определяется знаком силы Q, а их величина по высоте сечения меняется по параболическому закону и достигает наибольшей величины на нейтральной оси.

Для прямоугольного сечения I_x=,,

.

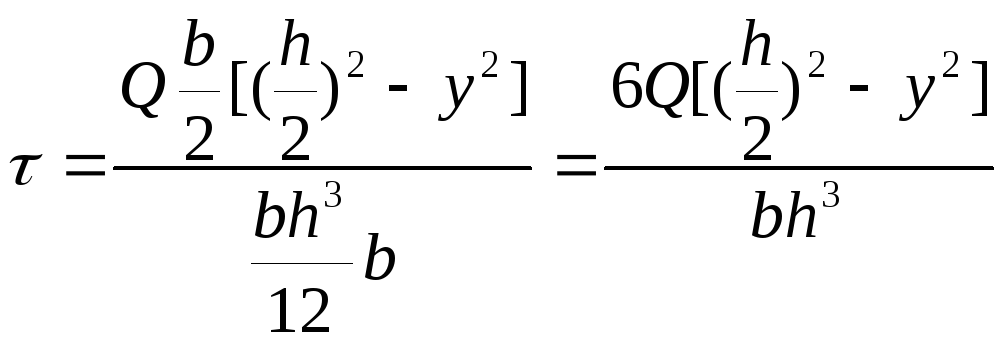Из этой формулы видно, что касательные напряжения по высоте меняются по закону квадратичной параболы. При у =τ = 0, при у = 0 .

На рис.6.21 показаны эпюры касательных напряжений для прямоугольного и круглого, на рис.6.22 для коробчатого и таврового сечений.

Рис.6.21

Рис.5.22

6.7 Расчёт балок на прочность по допускаемым напряжениям

Из полученных формул для напряжений при поперечном изгибе ,следует: в точках на поверхности балкиσ=|σ|_наиб , τ=0; в точках на нейтральной оси τ=|τ|_наиб, σ =0; в промежутке между этими точками и нормальные и касательные напряжения отличны от нуля. Таким образом, при расчетах на прочность при изгибе по допускаемым напряжениям следует рассматривать несколько опасных точек(рис.6.23).

Рис.6.23

Первая опасная точка на поверхности балки, в ней линейное напряженное состояние, для которого условие прочности записывается для сечения, где М=|М|_наиб

.

Вторая опасная точка рассматривается на нейтральной оси. В ней деформация чистого сдвига. Условие прочности записывается для сечения, где Q=|Q|_{наиб .}

При чистом сдвиге σ₁=τ, σ₃=-τ_. Используя четвертую теорию прочности, получим

σ_{экв I v} ==,или .

Третья опасная точка берется в промежутке между поверхностью и нейтральной осью. Так как в этой точке плоское напряженное состояние, главные напряжения найдутся по известным формулам:

. С учетом этих выражений запишем условия прочности:

по третьей теории σ_эквIII ==,

по четвертой - σ_{экв I v} ==.

Сечение, где располагается эта точка не столь определенно. Для его выбора, строго говоря, следует функцию исследовать на экстремум. Обычно таким сечением является сечение, где Q и М достаточно велики.