Семестровые компьютерные задания

62

Два числа z и z* называют комплексно – сопряженными, если их действительные части (и модули) одинаковы, а мнимые части (и аргументы) отличаются только знаком:

z = a + ib = (cos + i sin ) = exp (i ) ; z* = a - ib = (cos - i sin ) = exp (- i ) .

Векторы, изображающие комплексно – сопряженные числа, расположены симметрично относительно действительной оси.

Сложение и вычитание комплексных чисел z1 и z2 выполняются по пра-

вилу

z1 z2 = a1 + ib1 a2 + ib2 = (a1 a2) + i(b1 b2) ,

т.е. алгебраические действия над действительной и мнимой частью производятся независимо.

Умножение комплексных чисел z1 и z2 осуществляется по обычному правилу умножения многочленов

(a1 + ib1) (a2 + ib2) = (a1 a2 - b1 b2) + i(a1b2 + a2 b1) .

Наиболее удобна при умножении показательная форма представления комплексного числа

z1 z2 = 1 2 exp i( 1 + 2) .

Наконец, деление комплексных чисел аналогично случаю действительных чисел определяется как действие, обратное умножению

От “мнимости” в знаменателе удобно избавиться, для чего числитель и знаменатель умножают на число z2* , комплексно сопряженное делителю

Таким образом, деление сводится к умножению делимого на число, комплексно сопряженное делителю, с последующим делением на квадрат его модуля (действительное число). При использовании показательной формы все упрощается

z1 / z2 = ( 1 / 2) exp i( 1 - 2) .

63

2.Элементы математической теории поля. Градиент.

С математической точки зрения естественным обобщением оператора дифференцирования является следующий векторный оператор

где - единичные орты декартовых осей. С таким символом (набла) можно формально работать, как с обычным вектором, следя лишь за тем, чтобы справа от него стояла обычная функция от координат, на которую этот оператор действует.

Пусть мы имеем скалярное поле f (x,y,z) – скалярную функцию, дифференцируемую по каждой координате. Градиентом скалярного поля называют результат действия оператора на f (x, y, z) :

Таким образом, оператор “превращает” скалярное поле в векторное (x,y,z). С другой стороны, векторное поле 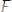(x,y,z) , которое можно представить как градиент скалярного поля, называют консервативным или потенциальным,

а f (x, y, z) – соответственно потенциалом. Криволинейный интеграл от такого поля по любой непрерывной траектории можно представить в виде

2

dl F (x, y, z) = f (x2, y2, z2) - f (x1, y1, z1) -

1

разности потенциалов на концах траектории. Отсюда следуют все хорошо известные свойства консервативного поля (независимость работы от формы траектории, обращение ее в нуль на замкнутом пути и т.д.)

Наглядно потенциальное поле можно изобразить линиями f (x,y,z)=const

– сечениями эквипотенциальных поверхностей, и нормальными к ним силовыми линиями, касательные к которым показывают направление вектора напряженности в данной точке. Чем больше в данной точке напряженность, тем гуще в окрестности этой точки пролегают силовые и эквипотенциальные линии. Геометрически вектор градиента в данной точке показывает направление наиболее быстрого роста потенциала, а модуль его пропорционален расстоянию между эквипотенциальными линиями. Напряженность же поля направлена в сторону наиболее быстрого убывания потенциала, а модуль ее совпадает с модулем градиента. Таким образом, напряженность направлена в сторону минимума потенциала.

64

3. Уравнение Шредингера и его решения для прямоугольной потенциальной ямы с бесконечно высокими стенками

В квантовой механике одномерное движение частицы описывается волновой функцией (x, t). Ее физический смысл состоит в том, что квадрат модуля этой, вообще говоря, комплексной функции определяет плотность вероятно-

сти w(x, t) обнаружения частицы в точке х в момент t w(x, t) = *(x, t) (x, t) = | (x, t)|2

Соответственно вероятность обнаружить частицу в конечном интервале, ограниченном точками a и b, можно определить как

W dxw x,t dx x,t 2

Поскольку в любой момент времени частица где-то находится, обнаружение ее в произвольной точке оси х есть достоверное событие. Отсюда вытекает условие нормировки волновой функции

b

dx x,t 2 1

a

Волновая функция является, вообще говоря, решением нестационарного уравнения Шредингера

где m – масса частицы, - постоянная Планка, U(x) – потенциальная энергия как функция координат. Состояние с точно фиксированной полной энергией Е называют стационарным, поскольку время его жизни в силу принципа неопределенности неограниченно

Е Т ; Е 0 Т .

Важно, что истинно стационарным может быть только основное состояние частицы, т.е. состояние с минимальной энергией. Любое состояние с большей энергией (возбужденное) может быть только квазистационарным, т.к. всегда существует некоторая вероятность его перехода в основное под влиянием внешних возмущений.

Волновая функция стационарного состояния может быть представлена в

Подставляя это выражение в исходное нестационарное уравнение Шредингера, получаем после простых преобразований уравнение для стационарных состояний

65

Решая последнее уравнение для конкретного вида потенциала U(x) , можно определить, во-первых, возможные значения полной энергии частицы (спектр энергии) Еn и, во-вторых, волновые функции так называемых чистых состояний n (x), т.е. состояний, соответствующих определенному значению квантового числа n . Отметим, что плотность вероятности чистого состояния от времени не зависит, поскольку

Однако в силу линейности последнего уравнения его решением будет любая линейная комбинация вида

m

x ci i x ,

i 1

где сi - постоянные коэффициенты. Такая функция определяет смешанное состояние частицы, причем упомянутые коэффициенты характеризуют вклад данного чистого состояния в “смесь”. В силу условия нормировки эти коэффициенты удовлетворяют условию

m

ci 2 1 ,

i 1

которое можно использовать для проверки найденных решений. При однократном измерении какой-либо физической величины в смешанном состоянии можно получить любое из набора значений этой величины, соответствующих чистым состояниям, дающим вклад в смешанное. Вероятность получения значения, соответствующего i – му чистому состоянию, равна сi2 . Среднее значение этой величины <a> по результатам множества измерений равно

При этом плотность вероятности для частицы в смешанном состоянии, в отличие от чистого состояния, от времени, строго говоря, зависит:

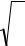
66

Первая группа слагаемых здесь постоянна, а вторая быстро осциллирует “вокруг нуля”.

В прямоугольной потенциальной яме с бесконечно высокими стенками, т.е. в потенциале вида

уравнение Шредингера для стационарных состояний принимает вид

Краевые условия для волновой функции (0) = (l) = 0 . Легко убедиться непосредственной подстановкой, что нормированные волновые функции чистых состояний имеют вид

а соответствующие значения энергетических уровней

Видим, что состояние частицы полностью определяется значением единственного квантового числа n .