Приложение скалярного произведения векторов к доказательству теорем

1. Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

□ Пусть в . Докажем, что.

З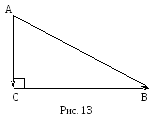апишем сначала векторное равенство для векторов, содержащих стороны, применив правило треугольника:

(рис. 13).

Возведем это векторное равенство в скалярный квадрат: .

По следствию из свойства А3⁰

.

Так как , то по свойству Г1⁰ . Применив Г2⁰, получаем:

.

Учитывая, что ,,(т.е. длина вектора- это длина отрезкаАВ), окончательно будем иметь:

. ■

2. Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.

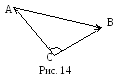□Докажем, что (рис. 14).

Представим вектор в виде разности векторов двух других сторон:

.

Возведем обе части этого векторного равенства в скалярный квадрат:

.

Далее воспользуемся следствием из свойства А3⁰:

.

Учитывая, что ,,и, получим:

,

откуда

. ■

Задания для самостоятельной работы

1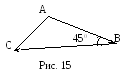. Найдите величину угла между векторамии(рис. 15).

2. Может ли величина угла между векторами равняться 270⁰?

3. Произведение - это число или вектор?

4. Верно ли равенство ? Если да, то докажите его справедливость для любых векторов,и; если нет, то приведите пример, подтверждающий этот вывод.

5. Докажите, пользуясь скалярным произведением, что диагонали ромба взаимно перпендикулярны, а диагонали квадрата не только взаимно перпендикулярны, но и равны.

Лекция 5 Нелинейные операции над векторами

§7. Понятие об ориентации пространства и плоскости

Пусть ,,- базис трехмерного векторного пространства.

Базис,,называетсяправым (левым), если при взгляде на плоскость векторов ииз конца третьего векторакратчайший поворот от первого векторако второму векторувиден как идущий против часовой стрелки (по часовой стрелке). На рис. 16 изображен правый базис, на рис. 17 – левый.

Можно дать и другие определения правого и левого базиса, например, такое: базис ,,называетсяправым (левым), если эти векторы, отложенные от одной точки, располагаются так же, как расставлены (примерно под прямым углом) пальцы правой (левой) руки: большой палец – по первому вектору , указательный – по, средний – по.

Мы будем пользоваться в дальнейшем первым определением.

Если два базиса правые (или левые), то говорят, что они одинаково ориентированы или имеют одинаковую ориентацию. Если один базис правый, а другой – левый, то говорят, что они противоположно ориентированы или имеют противоположную ориентацию.

Множество всех правых (всех левых) базисов в пространстве V называется правой (левой) ориентацией векторного пространства V.

Таким образом, в векторном пространстве ориентацию можно задать двумя способами: правую и левую. Векторное пространство, в котором выбрана ориентация, называется ориентированным. Как только в пространстве мы зададим базис, так сразу оно становится ориентированным.

В дальнейшем, если нет специальных оговорок, когда в пространстве выбран базис, будем считать, что он является правым.

Аналогично можно ввести понятие ориентированной плоскости. При этом базис ,на плоскости называетсяправым (левым), если кратчайший поворот от первого базисного вектора ко второму осуществляется против часовой стрелки (по часовой стрелке).