
- •Кафедра алгебры, геометрии, теории и методики обучения математике
- •Список рекомендуемой литературы
- •Элементы векторной алгебры Лекция 1 Векторы. Линейные операции над векторами
- •§1. Понятие вектора
- •Задания для самостоятельной работы
- •§2. Сложение и вычитание векторов
- •Правило треугольника
- •Правило параллелограмма
- •Правило многоугольника
- •Правило построения разности двух векторов
- •Задания для самостоятельной работы
- •§3. Умножение вектора на число
- •Свойства умножения вектора на число
- •Задания для самостоятельной работы
- •Лекция 3 Базис. Координаты вектора
- •§5. Базис. Координаты вектора в данном базисе
- •И их свойства
- •Свойства координат векторов
- •Задания для самостоятельной работы
- •Лекция 4 Нелинейные операции над векторами
- •§6. Скалярное произведение двух векторов
- •Геометрические свойства скалярного умножения векторов
- •Алгебраические свойства скалярного умножения векторов
- •Приложение скалярного произведения векторов к доказательству теорем
- •Задания для самостоятельной работы
- •Лекция 5 Нелинейные операции над векторами
- •§7. Понятие об ориентации пространства и плоскости
- •Задания для самостоятельной работы
- •Применение векторного произведения
- •Алгебраические свойства смешанного умножения векторов
- •Применение смешанного произведения
- •Задания для самостоятельной работы
- •§11. Основные аффинные и метрические задачи
- •Основные аффинные задачи
- •Основная метрическая задача
- •Задания для самостоятельной работы
- •Лекция 8 Формулы преобразования координат
- •§12. Преобразование аффинной системы координат
- •Частные случаи преобразования аффинной системы координат
- •Задания для самостоятельной работы
- •§13. Понятие направленного угла между векторами. Преобразование прямоугольной системы координат
- •Частные случаи преобразования прямоугольной системы координат
- •Задания для самостоятельной работы
- •§14. Полярные координаты
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •§16. Общее уравнение прямой и его частные случаи
- •Частные случаи общего уравнения прямой
- •Задания для самостоятельной работы
- •§17. Основные аффинные задачи, связанные с прямой на плоскости (обзор)
- •Задания для самостоятельной работы
- •Лекция 10
- •Задания для самостоятельной работы
- •§19. Основные метрические задачи, связанные с прямой на плоскости
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •§21. Общее уравнение плоскости
- •Задания для самостоятельной работы
- •§ 22. Лемма о параллельности вектора и плоскости. Частные случаи общего уравнения плоскости
- •Задания для самостоятельной работы
- •§ 23. Основные аффинные задачи, связанные с плоскостью (обзор)
- •Задания для самостоятельной работы
- •Лекция 12 Плоскость в прямоугольной системе координат
- •§ 24. Плоскость в прямоугольной системе координат. Основные метрические задачи, связанные с плоскостью
- •Задания для самостоятельной работы
- •Лекция 13 Прямая в пространстве. Различные задачи на прямые и плоскости в пространстве
- •§ 25. Различные уравнения прямой в пространстве
- •Задания для самостоятельной работы
- •§ 26. Основные аффинные задачи на прямые и плоскости
- •Задания для самостоятельной работы
- •§ 27. Основные метрические задачи на прямые и плоскости в пространстве
- •Задания для самостоятельной работы
Задания для самостоятельной работы
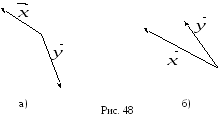
Определите (приближенно), чему равна величина направленного угла
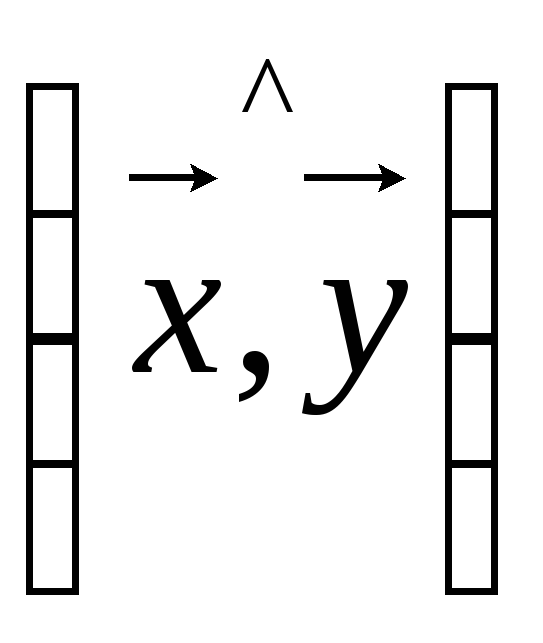 (рис. 48, а, б).
(рис. 48, а, б).
Может ли величина направленного угла между векторами быть равна
 ?
? ?
?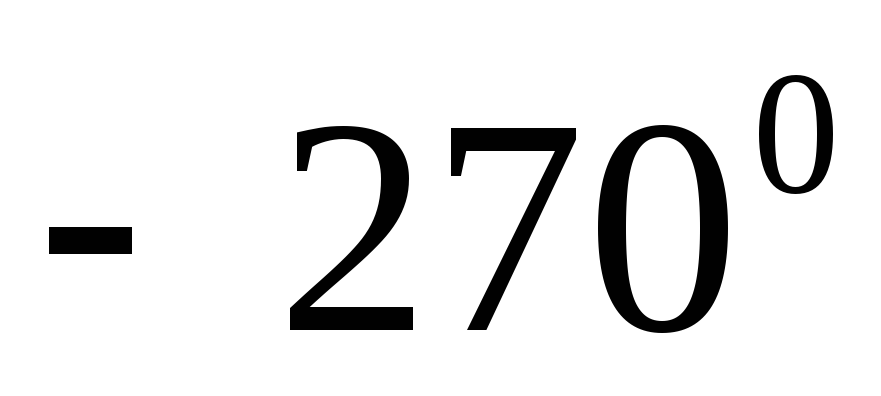 ?
Почему?
?
Почему?Найдите формулы преобразования прямоугольной системы координат, если координатные векторы повернуты на угол
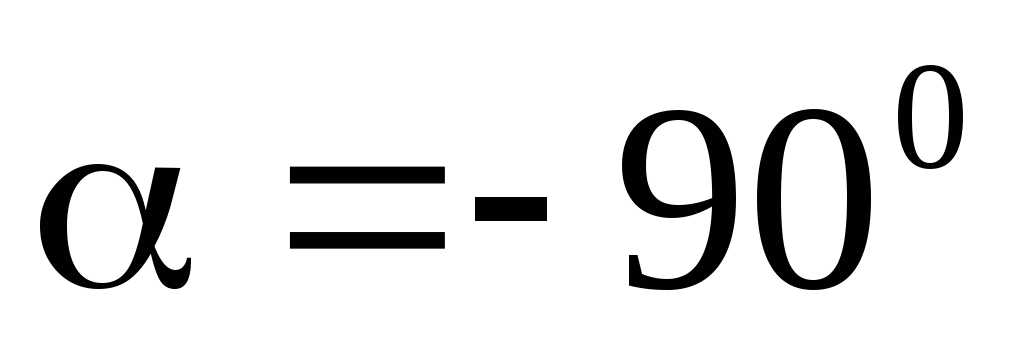 ,
а начало координат перенесено в точку
,
а начало координат перенесено в точку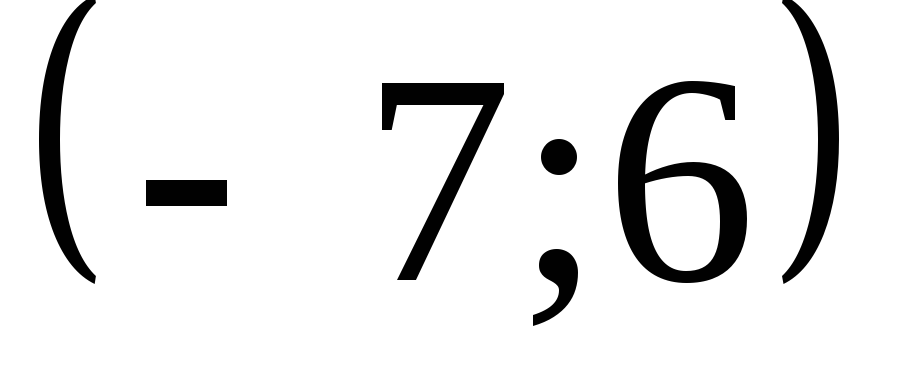 .
.Как по формулам преобразования координат узнать, какая система координат подвергается преобразованию: аффинная или прямоугольная?
Сделайте чертежи старой и новой систем координат для частных случаев преобразования прямоугольной декартовой системы координат.
§14. Полярные координаты
Если указано правило, по которому положение точек плоскости можно определить с помощью упорядоченных пар действительных чисел, то говорят, что на плоскости задана система координат. Кроме аффинной системы координат, которая была рассмотрена в §10, в математике часто применяют полярную систему координат на плоскости.
Система полярных координат вводится на ориентированной плоскости.
Пара, состоящая
из точки О
и единичного вектора
![]() ,
называетсяполярной
системой координат
и обозначается
,
называетсяполярной
системой координат
и обозначается
![]() или
или![]() .
Направленная прямая
.
Направленная прямая![]() называетсяполярной
осью, точка
О -
полюсом
(рис. 49).
называетсяполярной
осью, точка
О -
полюсом
(рис. 49).
П
О устьМ –
произвольная точка плоскости. Расстояние
устьМ –
произвольная точка плоскости. Расстояние
![]() от точкиО
до точки М
называется полярным
радиусом точки М.
от точкиО
до точки М
называется полярным
радиусом точки М.
|
|
Н аправленный
угол
аправленный
угол![]() называетсяполярным
углом точки М (рис.
50).
называетсяполярным
углом точки М (рис.
50).
|
|
П олярный
радиус
и полярный угол
называются полярными координатами
точки М.
олярный
радиус
и полярный угол
называются полярными координатами
точки М.
На рис. 51 построены
точки
![]() ,
,![]() ,
,![]() по их полярным координатам.
по их полярным координатам.
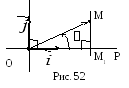
Выведем формулы перехода от полярных координат к прямоугольным декартовым и обратно.
Пусть
![]() - полярная система координат на
ориентированной плоскости,
- полярная система координат на
ориентированной плоскости,![]() ,
,![]() в
в![]() .
Присоединим к полярной системе
.
Присоединим к полярной системе![]() единичный вектор
единичный вектор![]() ,
ортогональный вектору
,
ортогональный вектору![]() так, чтобы базис
так, чтобы базис![]() ,
,![]() был правым (рис. 52).
был правым (рис. 52).
![]() ,
,
![]() .
.
Пусть М(х;у)
в
![]() .
Тогда
.
Тогда![]() ;
;![]() (рис. 52).
(рис. 52).
|
|
Возведем обе части этих равенств в квадрат и сложим:
![]() ,
откуда
,
откуда
![]() (корень берется со знаком «+», т.к.
(корень берется со знаком «+», т.к.![]() ).
).![]()
![]()
![]() ;
;![]() .
.
|
|
З
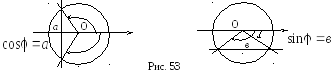 амечание.
При решении задач на переход от
прямоугольных декартовых координат к
полярным недостаточно найти только
амечание.
При решении задач на переход от
прямоугольных декартовых координат к
полярным недостаточно найти только
![]() или только
или только![]() ,
т.к. по одной тригонометрической функции
определить полярный угол однозначно
невозможно: в промежутке
,
т.к. по одной тригонометрической функции
определить полярный угол однозначно
невозможно: в промежутке![]() существуют два угла с одинаковыми
косинусами (два угла с одинаковыми
синусами) (рис. 53). Поэтому правильно
найти полярный угол
вы сможете, только если одновременно
вычислите
существуют два угла с одинаковыми
косинусами (два угла с одинаковыми
синусами) (рис. 53). Поэтому правильно
найти полярный угол
вы сможете, только если одновременно
вычислите
![]() и
и![]() .
.
Задания для самостоятельной работы
Может ли полярный угол быть равным
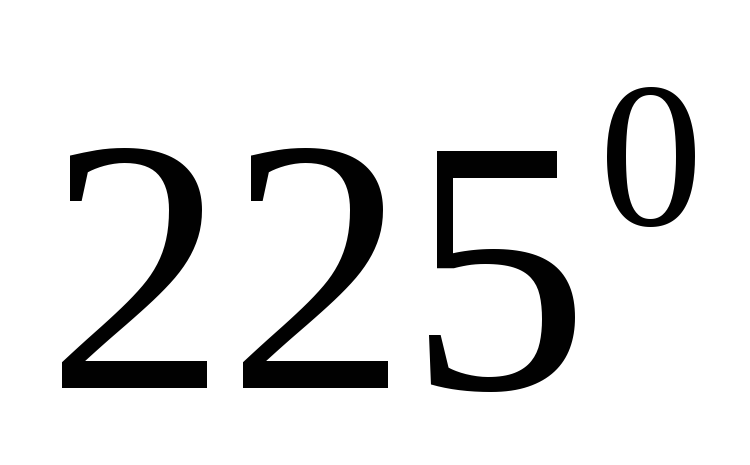 ?
?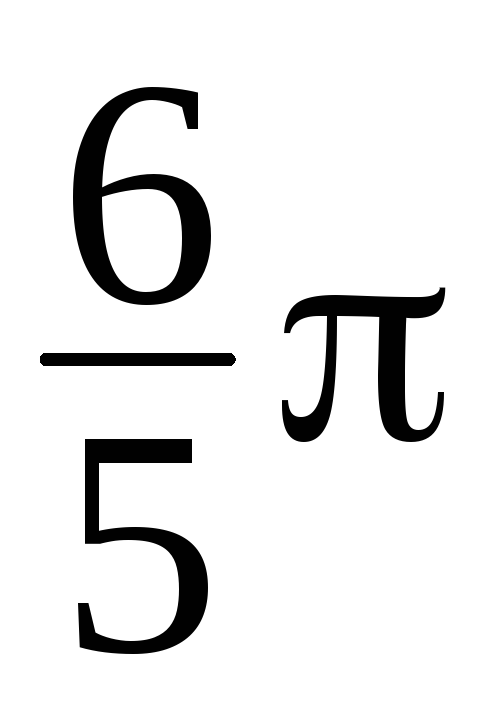 ?
?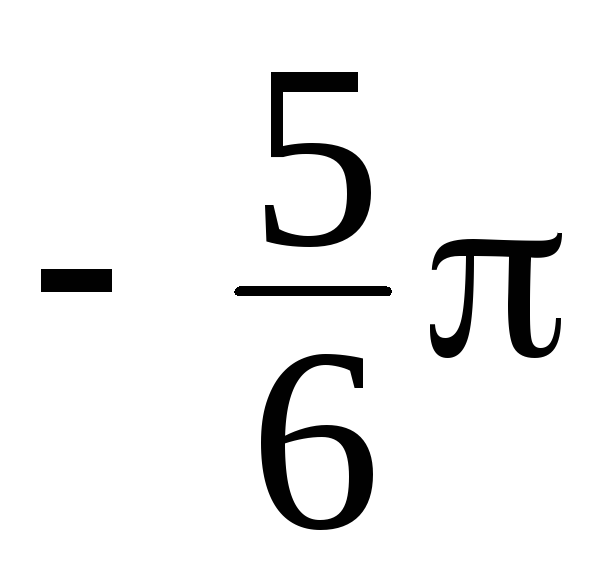 ?
?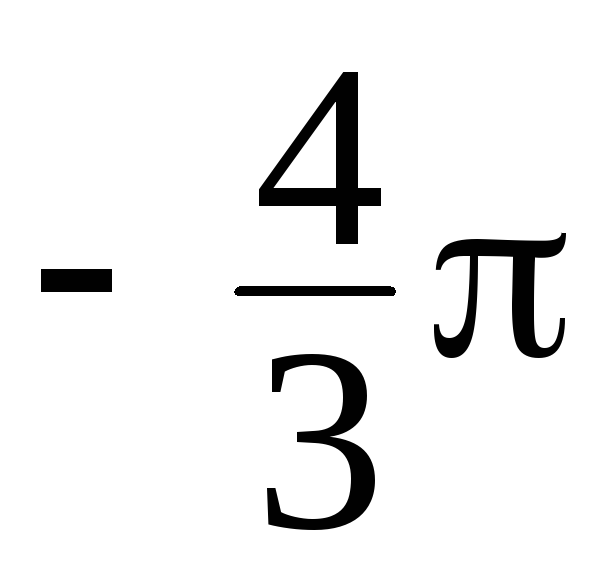 ?
Почему?
?
Почему?Постройте точки
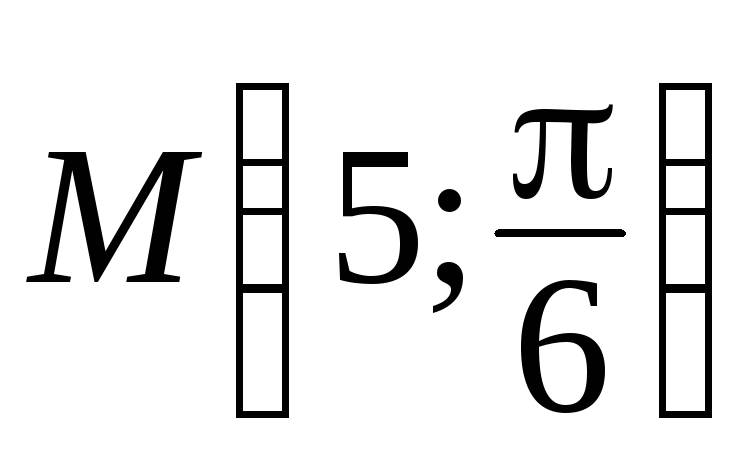 ,
,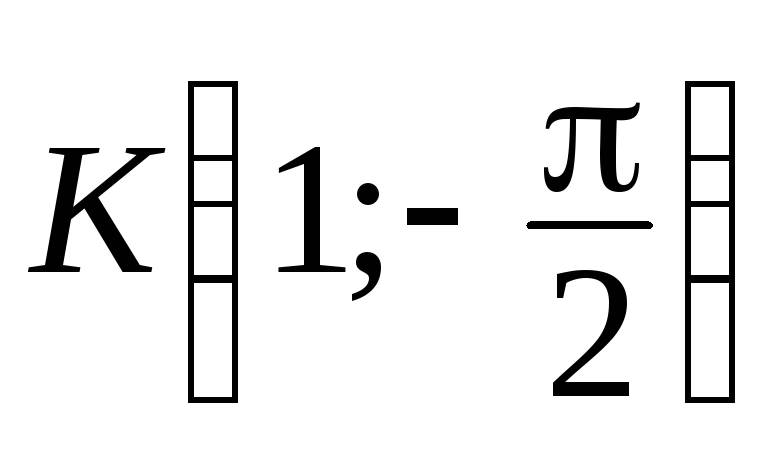 ,
,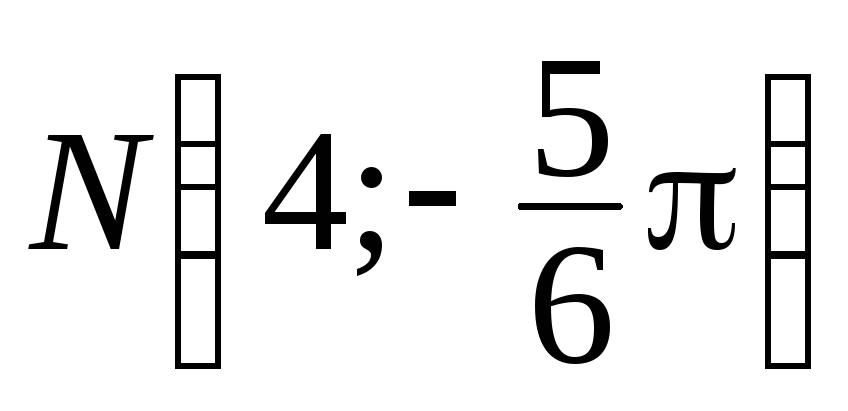 .
.Найдите прямоугольные декартовы координаты точки
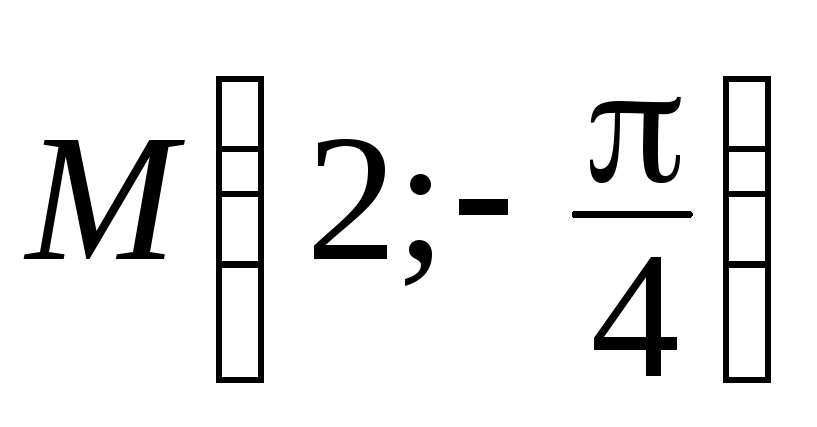 .
.Известны прямоугольные декартовы координаты точки
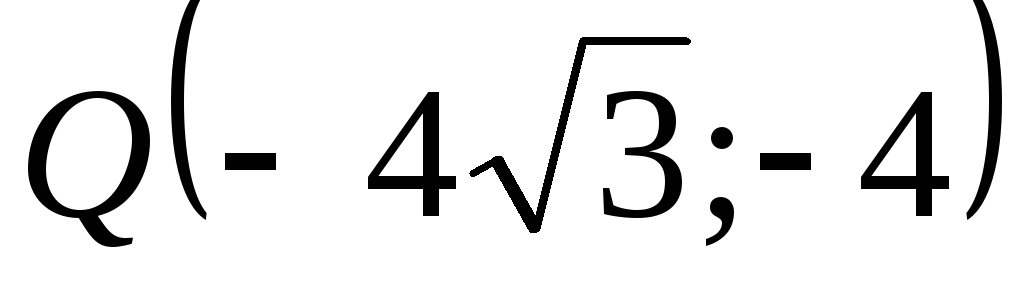 .
Не выполняя построения точкиQ,
найдите ее полярные координаты.
.
Не выполняя построения точкиQ,
найдите ее полярные координаты.Выведите формулу расстояния между двумя точками
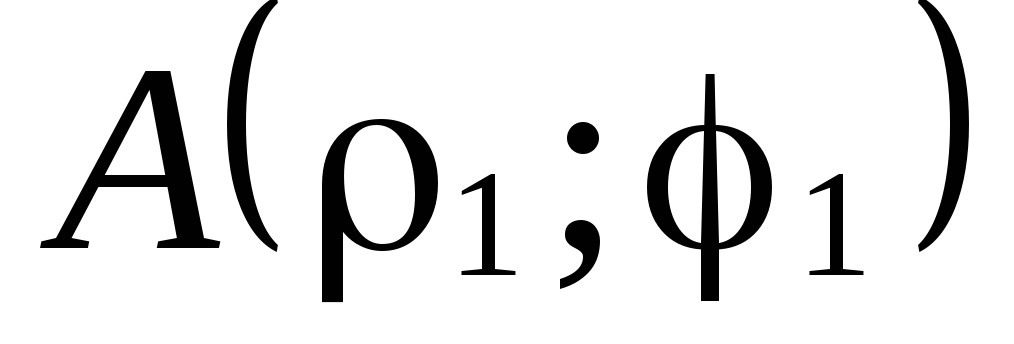 и
и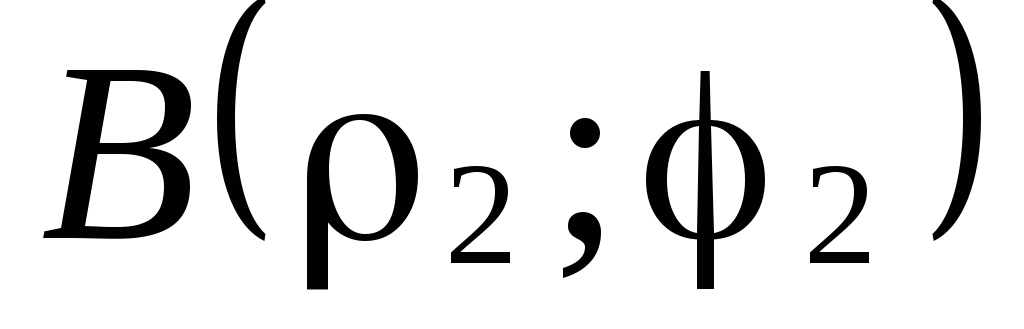 ,
заданными полярными координатами.
,
заданными полярными координатами.
Прямая линия на плоскости
Лекция 9
Прямая в аффинной системе координат
§15. Различные уравнения прямой
Говорят, что
уравнение
![]() естьуравнение
линии
естьуравнение
линии
![]() ,
если выполняются два условия:
,
если выполняются два условия:
если точка
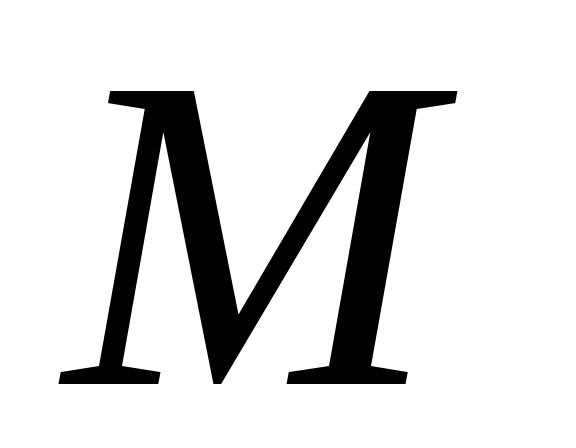 принадлежит линии
принадлежит линии ,
то ее координаты удовлетворяют уравнению
,
то ее координаты удовлетворяют уравнению ;
;если координаты точки
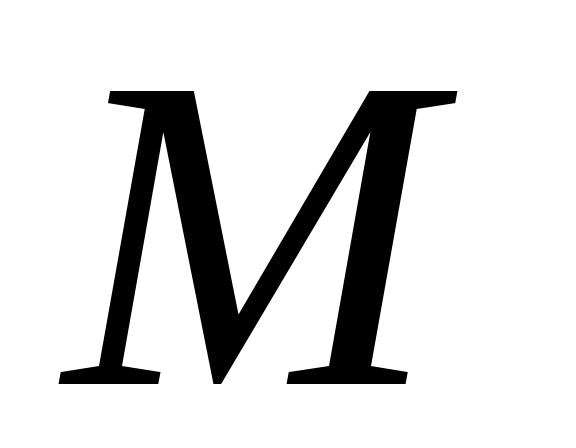 удовлетворяют уравнению
удовлетворяют уравнению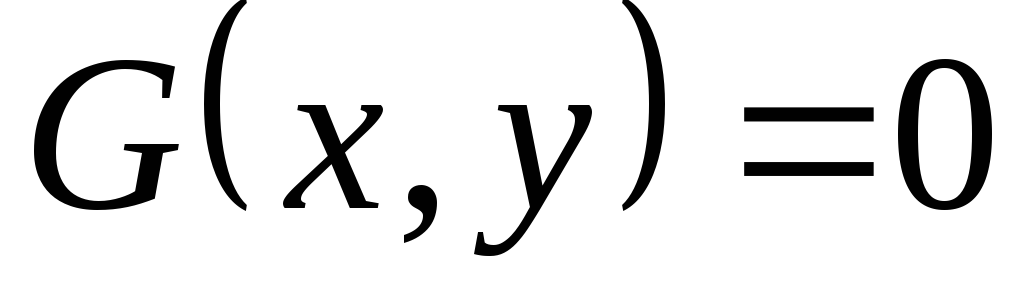 ,
то
,
то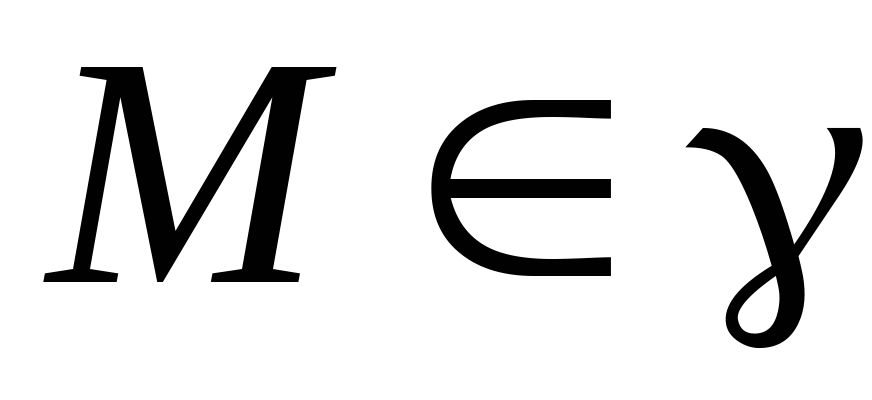 .
.
Заметим, что условие 2) можно заменить на эквивалентное ему условие 2*):
2*)
если
![]() ,
то ее координаты не удовлетворяют
уравнению
,
то ее координаты не удовлетворяют
уравнению![]() .
.
Линия на плоскости
называется алгебраической,
если в какой-либо аффинной системе
координат уравнение этой линии можно
представить в
![]() ,
где
,
где![]() многочленот переменных
многочленот переменных![]() и
и![]() ,
т.е. сумма членов вида
,
т.е. сумма членов вида
![]() ,
,![]() .
.
Число
![]() называетсястепенью
члена
называетсястепенью
члена
![]() ,
где
,
где
![]() .
.
Наивысшая степень
членов многочлена ![]() называется степенью
этого многочлена.
Например, степень многочлена
называется степенью
этого многочлена.
Например, степень многочлена ![]() равна 7.
равна 7.
Порядком
алгебраической линии,
заданной уравнением
![]() ,
называется степень многочлена
,
называется степень многочлена![]() .
.
Из школьного курса известно, что прямая линия является линией первого порядка, а окружность, гипербола и парабола – линиями второго порядка.
Рассмотрим на
плоскости прямую линию. Любой ненулевой
вектор, параллельный данной прямой,
называется ее направляющим
вектором.
Направляющий вектор прямой
![]() будем обозначать через
будем обозначать через![]() .
Прямая имеет бесконечное множество
направляющих векторов. Любые два из них
коллинеарны (рис. 54).
.
Прямая имеет бесконечное множество
направляющих векторов. Любые два из них
коллинеарны (рис. 54).
Прямая на плоскости однозначно задается точкой и направляющим вектором или двумя точками.
Выведем несколько
уравнений прямой на плоскости в аффинной
системе координат
![]() .
.
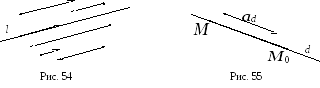
Каноническое уравнение прямой.
Пусть прямая
![]() задана точкой
задана точкой![]() и направляющим вектором
и направляющим вектором![]() (рис. 55). Этот факт будем обозначать так:
(рис. 55). Этот факт будем обозначать так:![]() .
.
Если точка ![]() принадлежит прямой
принадлежит прямой
![]() ,
то
,
то![]() .
Находим координаты вектора
.
Находим координаты вектора![]() .
Далее применяем условие коллинеарности
двух векторов в координатах (см. § 5,
свойство координат векторов 50):
.
Далее применяем условие коллинеарности
двух векторов в координатах (см. § 5,
свойство координат векторов 50):
![]() ,
если
,
если
![]() ;
;
![]() ,
если
,
если
![]() ;
;
![]() ,
если
,
если
![]() .
.
Е сли
сли![]() ,
то
,
то
![]() ||
||![]() .
Следовательно,
.
Следовательно,
![]() ,
если
,
если
![]() ;
;
![]() ,
если
,
если
![]() ;
;
![]() ,
если
,
если
![]() .
.
И
![]() принадлежит прямой
принадлежит прямой
![]() тогда и только тогда, когда ее координаты
удовлетворяют уравнению
тогда и только тогда, когда ее координаты
удовлетворяют уравнению
![]() (если
(если
![]() );
(10)
);
(10)
![]() (если
(если
![]() );
(11)
);
(11)
![]() (если
(если
![]() ).
(12)
).
(12)
Каждое из уравнений (10), (11) и (12) называется каноническим уравнением прямой на плоскости.
В уравнениях
(10)-(12)
![]()
координаты фиксированной точки
координаты фиксированной точки
![]() прямой
прямой![]() ;
;![]()
координаты направляющего вектора прямой
координаты направляющего вектора прямой
![]() ;
;![]()
текущие
координаты произвольной точки прямой
текущие
координаты произвольной точки прямой
![]() .
.
2. Параметрическое уравнение прямой.
Пусть прямая
![]() задана точкой
задана точкой![]() и направляющим вектором
и направляющим вектором![]() .
.
![]() (рис. 54)
(рис. 54)
![]() (по теореме о коллинеарных векторах).
(по теореме о коллинеарных векторах).
З
![]()
![]() или
(13)
или
(13)
Система уравнений
(13) называется параметрическим
уравнением прямой на плоскости.
Действительное число
![]() называетсяпараметром.
Геометрический
смысл
параметра
называетсяпараметром.
Геометрический
смысл
параметра
![]() состоит в следующем: для любой точки
состоит в следующем: для любой точки![]() существует
единственный параметр
существует
единственный параметр
![]() ,
удовлетворяющий уравнениям (13), и обратно,
,
удовлетворяющий уравнениям (13), и обратно,![]() и
и![]() .
.
3. Уравнение прямой, заданной двумя точками.
Пусть
![]() (рис. 56). Тогда в качестве направляющего
вектора прямой
(рис. 56). Тогда в качестве направляющего
вектора прямой![]() можно взять вектор
можно взять вектор![]() ,
т.е.
,
т.е.
![]()
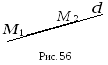 .
.
Т
![]()
![]() задана точкой
задана точкой![]() и направляющим вектором
и направляющим вектором![]() .
Применяем каноническое уравнение прямой
(10) (см. пункт 1):
.
Применяем каноническое уравнение прямой
(10) (см. пункт 1):
(14)
Уравнение (14)
называется уравнением
прямой, заданной на плоскости двумя
точками
![]() и
и
![]() .
.
Заметим, что если
![]() или
или![]() ,
то применяем частные случаи (11) или (12)
канонического уравнения прямой.
,
то применяем частные случаи (11) или (12)
канонического уравнения прямой.
4. Уравнение прямой в «отрезках».
П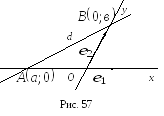 усть
прямая
усть
прямая![]() пересекает ось
пересекает ось![]() аффинной системы координат
аффинной системы координат![]() в точке
в точке![]() ,
ось
,
ось![]()
в точке
в точке
![]() ,
где
,
где![]() (рис. 57).
(рис. 57).
Применяя уравнение прямой, заданной двумя точками А и В, получим:
![]() ;
;
![]() ;
;
![]() ,
,
откуда получаем уравнение:
![]() (15)
(15)
Уравнение (15) называется уравнением прямой «в отрезках».
Геометрический
смысл а
и
в
в уравнении прямой «в отрезках»: а
– это абсцисса точки пересечения прямой
![]() с осью
с осью![]() ,в
– ордината точки пересечения прямой
,в
– ордината точки пересечения прямой
![]() с осью
с осью![]() аффинной системы координат.
аффинной системы координат.
5. Уравнение прямой, заданной точкой и угловым коэффициентом.
П
 усть
усть![]()
прямая, не параллельная оси
прямая, не параллельная оси
![]() (рис. 58),
(рис. 58),![]()
направляющий вектор прямой
направляющий вектор прямой
![]() .
Так как
.
Так как![]() ||
||![]() ,
а
,
а![]() ,
то
,
то![]() ||
||![]() .
Следовательно,
.
Следовательно,![]() ||
||![]() .
Поэтому
.
Поэтому![]() (см. условие коллинеарности векторов в
координатах).
(см. условие коллинеарности векторов в
координатах).
Число
![]() называетсяугловым
коэффициентом
прямой
называетсяугловым
коэффициентом
прямой
![]() .
.
Угловой коэффициент прямой не зависит от выбора направляющего вектора этой прямой (попробуйте доказать это самостоятельно).
З амечание.
Если прямая
амечание.
Если прямая
![]() задана в прямоугольной системе координат
задана в прямоугольной системе координат![]() ,
то
,
то![]() имеет простойгеометрический
смысл:
имеет простойгеометрический
смысл:
![]() ,
где
,
где![]()
угол наклона прямой
угол наклона прямой
![]() к оси
к оси![]() ,
т.е. направленный угол
,
т.е. направленный угол![]() (рис. 59).
(рис. 59).
Пусть прямая
![]() задана точкой
задана точкой![]() и угловым коэффициентом
и угловым коэффициентом![]() .
Запишем каноническое уравнение прямой
.
Запишем каноническое уравнение прямой![]() :
:
![]()
и преобразуем его:
![]() ;
;![]() ;
учитывая, что
;
учитывая, что![]() ,
получим:
,
получим:
![]() (16)
(16)
Уравнение (16) называется уравнением прямой, заданной точкой и угловым коэффициентом.
6. Уравнение прямой с угловым коэффициентом.
Пусть
![]()
угловой коэффициент прямой
угловой коэффициент прямой
![]() .
Применяя уравнение (16), получим:
.
Применяя уравнение (16), получим:![]() ,
т.е.
,
т.е.
![]() .
(17)
.
(17)
Уравнение (17) называется уравнением прямой с угловым коэффициентом.
В уравнении (17) в
– это ордината точки пересечения прямой
![]() с осью
с осью![]() .
.
