5.2.6. Расчёт зубчатых колес на контактную прочность

Для силовых передач модуль определяется по формулам.

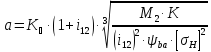(20)

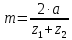(21)

где 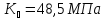для стальных прямозубых цилиндрических колес.

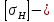допускаемое контактное напряжение. .

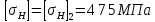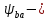коэффициент ширины колеса,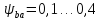. Выберем.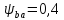

Выполним расчет по формулам

,

,

,

,

,

,

,

.

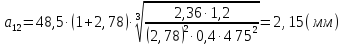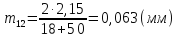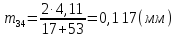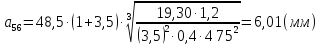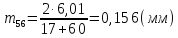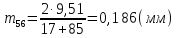Округляем до минимального значения модуля для передач, получаем

.

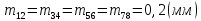По расчетам выберем наибольшие значения модулей для передач.

.

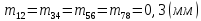Из конструктивных соображений, также по согласованию с преподавателем округлим полученное значение до ряда предпочтительных чисел, до 0,5мм, в большую сторону, поскольку это только увеличит прочность передач.

Проверочный расчёт на контактную прочность показывает, что зубчатые колёса удовлетворяют условиям прочности.

5.3. Геометрический расчёт кинематики проектируемой конструкции

По проведенным кинематическому и прочностному расчетам можно сделать расчет геометрических параметров зубчатых колес (см. рис.2.) , входящих в проектируемы привод.

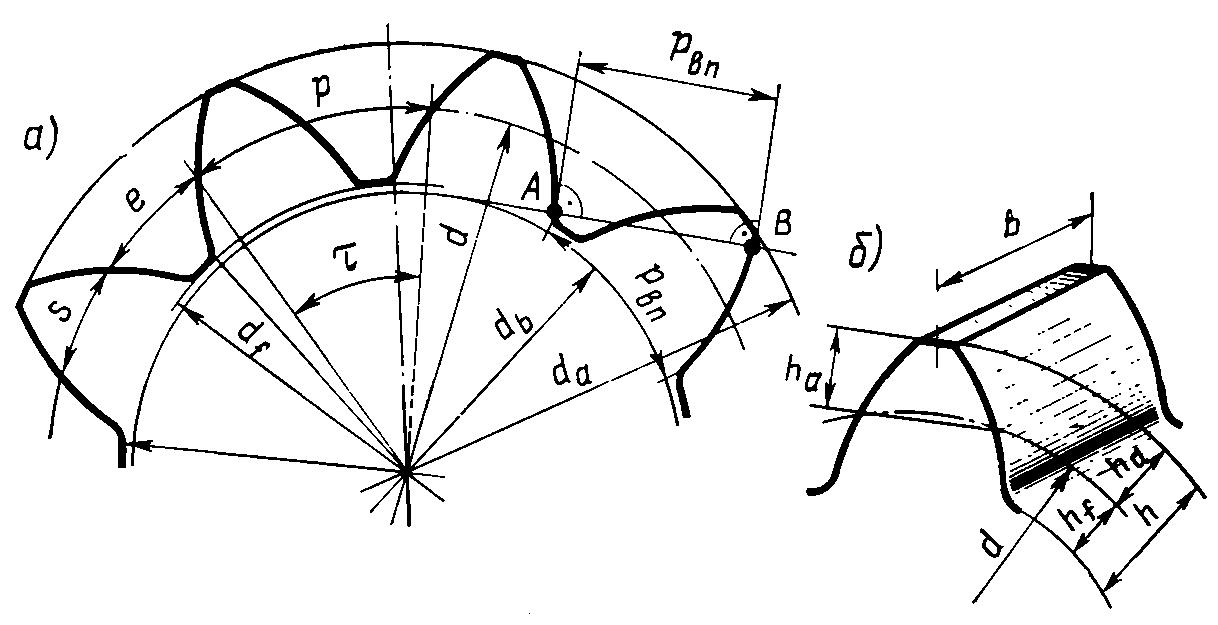
Рис.2.

Делительный диаметр

d₁=m·Z₁/cosβ=m·Z₁ т.к. колесо прямозубое, то β=0 (22)

Диаметр вершин зубьев

d_a=m·z/cosβ+2·m· (h_a+x₁₂)=m· (z+2) т.к. h_a=1, x₁₂=0 (23)

Диаметр впадин

d_f=m·z/cosβ-2·m· (h_a+c-x₁₂)=m(z-2-2·c); Так как m≤0.5, то c=0.5. (24)

Ширина колес

b₂ = ψ_bm·m, (25)

где

ψ_bm – коэффициент, равный отношению ширины зубчатого венца к модулю, ψ_bm =10.

Ширина шестерни

b₁ = b₂ + 1,5m (26)

Делительное межосевое расстояние

a_ω=0.5·m·(Z₁+Z₂)/cosβ=0.5·m·(Z₁+Z₂) (27)

Таблица 5.

№	1	2	3	4	5	6	7	8
Z	18	50	17	53	17	60	17	85
d1, мм	9	25	8,5	26,5	8,5	30	8,5	42,5
da, мм	10	26	9,5	27,5	9,5	31	9,5	43,5
df, мм	7,5	23,5	7	25	7	28,5	7	41
b, мм	5,75	5	5,75	5	5,75	5	5,75	5
aω, мм	17		17,5		19,25		25,5

На этом этапе можно изобразить кинематическую схему редуктора, а также начать предварительную разметку привода.

6. Проектировочный расчет валов и опор

Целесообразно выделить наиболее нагруженный вал в редукторе и выполнить расчёт для него. Самыми нагруженными валами являются последние валы: пятый (выходной) и четвёртый. Расчёт проведём для четвёртого (предпоследнего) вала.

6.1. Проектировочный расчет вала

Момент кручения равен

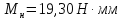
Назначим материал Сталь 45.

Диаметр валика определяется из условия

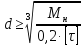(28)

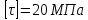- среднее значение касательных напряжений для стальных валов.

Расчет диаметра всех валов дает:

№ вала Параметр	1 (входной)	2	3	4	5
Mкр, Н∙мм	2,36	6,38	19,30	65,55	318
d, мм	0,83	1,17	1,68	2,60	4,30

Из технологических соображений и по условию ТЗ назначаем диаметры валов из стандартного ряда по ГОСТ 12081-72:

№ вала	1й вал	2й вал	3й вал	4й вал	5й вал
d, мм	4.0	4.0	4.0	5.0	10.0

6.1.1. Расчет вала на статическую прочность

Для расчёта выберем предпоследний вал, как наиболее нагруженный.

При расчете принимаем:

1. Ширина шестерни: 7 мм

2. Ширина колеса: 5 мм

3. Расстояние между шестернёй и опорой 2 мм

4. Расстояние между колесом и опорой 23,5 мм

5. Ширина опоры 3 мм

6. Расстояние между колесом и шестерней 2,5мм

Из этого следует, что общая длина вала 46 мм

Расчет сил, действующих на вал, ведем по формулам:

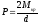, (29)

где

d– диаметр начальной окружности колеса или шестерни

Принимаем d,равным диаметру делительной окружности, т. к.x= 0

M_кр– крутящий момент на валу

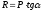, (30)

где α= 20

Значения сил, приложенных к валу:

Pк = 4,37 Н	Rк = 1,59 Н
Pш = 15,42 Н	Rш = 5,61 Н

Изобразим расчетную схему для вала:

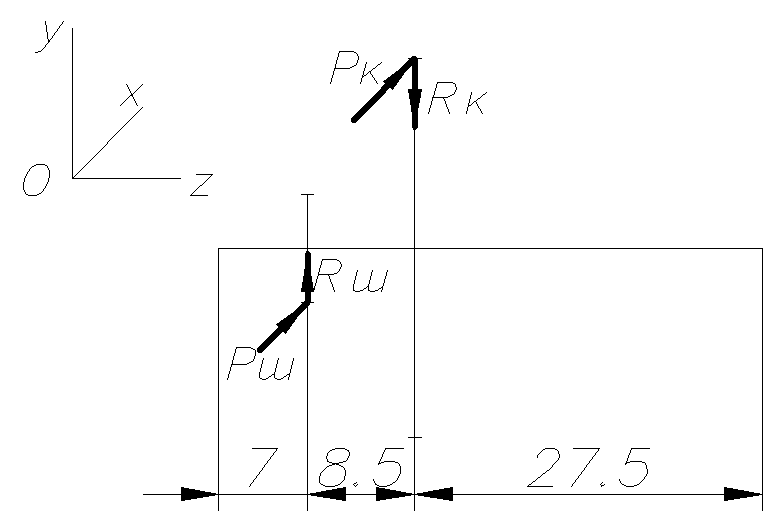
Рис.3.

Проекции сил, приложенных к валу на плоскость ZX:

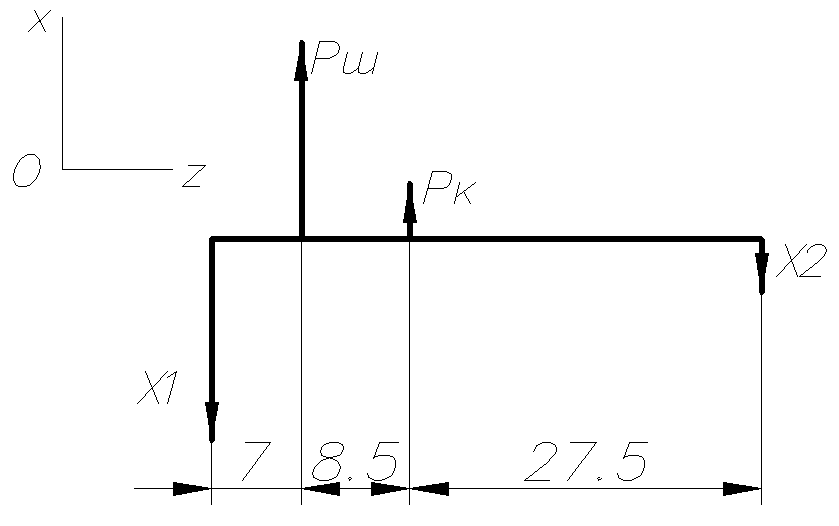
Рис.4.

Проекции сил, приложенных к валу на плоскость ZY:

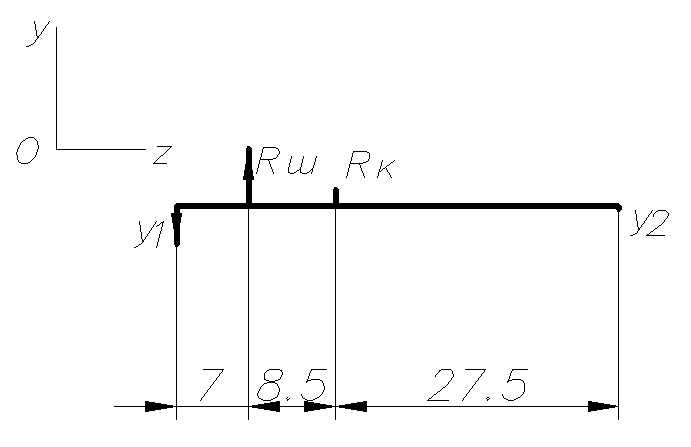
Рис.5.

Для определения неизвестных реакций X₁,X₂,Y₁,Y₂составим системы уравнений равновесия вала:

Плоскость ZX: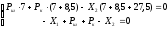

Плоскость ZY: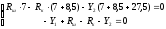

В результате решения уравниний находим:

X1 = 15,70 Н	Y1 = 3,68 Н
X2 = 4,09 Н	Y2 = 0,34 Н

Эпюры моментов, действующих на вал (все моменты показаны в [Н∙мм]):

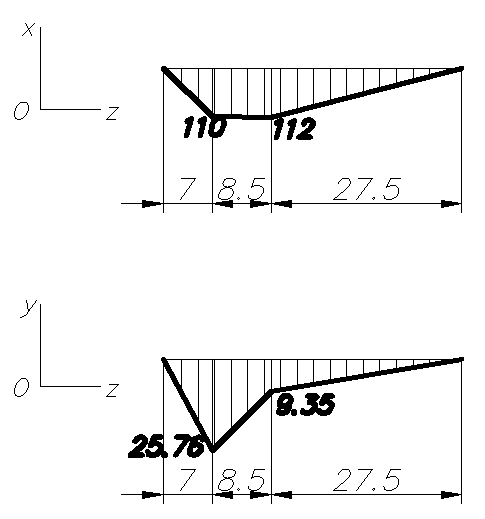
Рис.6.