Название основных типов сополимеров

Тип (класс) сополимера	Соеди-нительное слово	Исходные мономеры	Названия по номенклатуре
			систематической	альтернативной
Неустанов-ленный	-со-	стирол, метилметакрилат	поли(стирол-со-метилметакрилат)	сополи(стирол/метилметакрилат)
Статисти-ческий	-стат-	стирол, бутадиен стирол, бутадиен, акрилонитрил	поли(стирол-стат-бутадиен), поли(стирол-стат-бутадиен-стат-акрилонитрил)	стат-сополи(стирол/ бутадиен),стат-сополи- (стирол/ бутадиен/акрило-нитрил)
Случайный	-сл-	этилен, винилацетат	поли(этилен-сл-винилацетат)	сл-сополи(этилен/ви-нилацетат)
Чередую-щийся	-чер-	стирол, малеиновый ангидрид	поли(стирол-чер-малеиновый ангидрид)	чер-сополи(стирол/ малеиновый ангидрид)
Периоди-ческий	-период-	этиленфенилфос-фонит, метилакри-лат, двуокись углерода	поли(этиленфенилфосфонит-период-метилакрилат-период-диоксид углерода)	период-сополи(этилен-фенилфосфонит/метил-акрилат/диоксид углерода)
Блок-сополимер	-блок-	стирол, бутадиен, метилметакрилат	поли(стирол-блок-бутадиен-блок-метилметакрилат	блок-сополи(стирол/бутадиен/метилметак-рилат
Привитой сополимер	-прив-	бутадиен, стирол	полибутадиен-прив-полистирол	прив-сополи(бутадиен/ стирол)

1.4. Молекулярно-массовые характеристики полимеров

1.4.1. Распределение макромолекул по молекулярным массам

С учетом знания химической структуры, т.е. конфигурации элементарного звена и цепи в целом, одной из важнейших характеристик полимеров является молекулярная масса. Молекулярная масса, конфигурация и гибкость макромолекулы предопределяют все остальные физические характеристики изолированных макромолекул, такие как размеры, форма, способность к спонтанному или вынужденному изменению формы. Молекулярная масса лежит в основе определения понятий грамм-молекулы (моля) и мольных включений (т.е. физико-химических характеристик при расчете на один моль) – таких, как молярные (мольные) концентрации, объем, теплоемкость, электропроводность, теплота реакции и т.д. Молекулярная масса входит во многие уравнения и соотношения, выражающие связь между различными физико-химическими величинами. Многие универсальные законы и величины, не зависящие от индивидуальных свойств вещества, приведены к одному молю и, следовательно, также содержат молекулярную массу в скрытом виде.

Согласно ИЮПАК рекомендуется применять два основных термина⁵:

молярная масса (М) - масса вещества, деленная на его количество (масса одного моля вещества);

относительная молекулярная масса или молекулярный вес (М_r) - отноше­ние средней массы вещества, соответствующей его формуле, к 1/12 массы яд­ра атома углерода ¹²С.

Молярная масса выражается в г/моль или кг/моль. Первое предпочти­тельней, поскольку при этом численные значения молярной массы и относи­тельной молекулярной массы вещества совпадают. Относительная молеку­лярная масса или молекулярный вес - безразмерная величина. Индекс «r» в ее обозначении обычно опускается, если это не ведет к путанице.

Под термином «молеку­лярная масса», ее сокращенными обозначениями ММ и М будем подразумевать безразмерную величину - относительную молекулярнаую массу.

Практически все полимеры за редким исключением содержат макромо­лекулы разной молекулярной массы. Это специфическое свойство полиме­ров называется полидисперсностью, а макромолекулы одного химического состава, но разной молекулярной массы называются полимергомологами. Основными молекулярно-массовыми характеристиками полидисперсных полимеров являются средние молекулярные массы (ММ), функции молекулярно-массового распределения (ММР) и кривые распределения, соответст­вующие этим функциям.

Таким образом, для высокомолекулярных соединений понятия о молекуле и молекулярной массе имеют две особенности:

1) омеченная выше полидисперсность;

2) большая молекулярная масса. Разрыв цепи полимера приводит к изменению его полидисперсности и снижению средних значений молекулярных масс, но не к потере основных химических свойств.

Существует огромное число полимеров, для которых понятие «молекула» и «молекулярная масса» теряют общепринятый смысл. Эти вещества, имеющие пространственную «сверхмолекулярную структуру», такие как алмаз, отвержденные полиэфиракрилаты, фенолальдегидные, эпоксидные, меламиновые смолы, вулканизованные каучуки. Термин «молекулярная масса» здесь неприменим и для них можно ограничиться определением густоты пространственной сетки или массы сегмента между узлами.

В простейших случаях ММР полимера может быть представлено таблич­ными значениями. Для того, чтобы количественно охарактеризовать рас­пределение полимера по ММ, необходимо рассчитать относительное коли­чество фракций, содержащих макромолекулы одинаковой ММ. Это можно сделать двумя способами - исходя из числа или суммарной массы макромо­лекул. В первом случае находят числовую долю фракции:

, (1.3)

где n_i - число макромолекул фракции i, имеющих ММ, равную М_i, - общее число макромолекул в полимере. Во втором случае находят массовую долю:

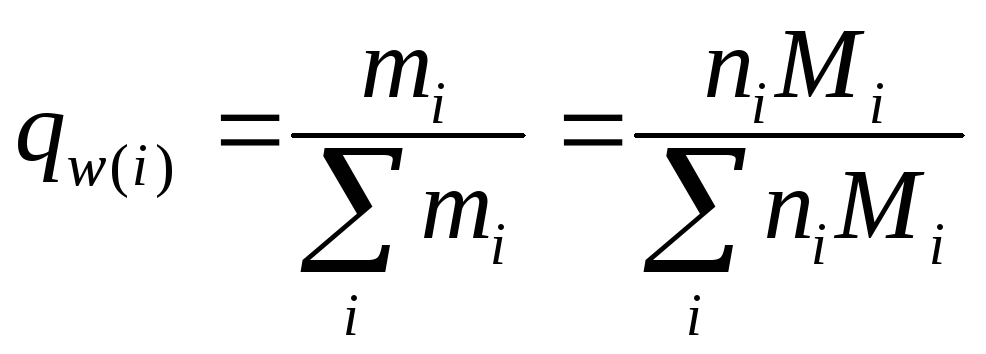, (1.4)

где m_i = п_iМ_i - масса фракции i, т. е. суммарная масса макромолекул, имею­щих ММ, равную М_i; - общая масса полимера.

Рассмотрим в качестве примера образец полидисперсного полимера общей массой 1 г, состоя­щий из пяти фракций массой 0,2 г каждая. Ниже приведены данные, харак­теризующие ММР полимера в рассматриваемом примере.

i	№ фракции
	1	2	3	4	5
Mi	0,4·104	0,8·104	2·104	6·104	105
qn	0,554	0,277	0,111	0,036	0,022
qw	0,2	0,2	0,2	0,2	0,2

Видно, что картина распределения весьма существенно зависит от спосо­ба оценки относительного количества фракций. В случае числового распре­деления более существенен вклад фракций с меньшей ММ, в случае массо­вого распределения - вклад фракций с большей ММ.

Средняя ММ полидисперсного полимера является средневзвешенной величиной, вклад в которую каждой из фракций определяется ее ММ и относительным количеством. Следовательно, для полидисперсного полимера характерны две средние ММ - среднечисловая :

(1.5)

и среднемассовая :

. (1.6)

Из выражения (1.5) следует, что среднечисловая ММ равна общей массе макромолекул, деленной на их число. Расчеты по данным таблицы приводят к =1,110⁴, = 3,8410⁴, т.е. >. Как мы увидим в дальнейшем, это общее правило для полидисперсных полимеров.

Существуют дискретные и непрерывные функции распределения. Дискретная дифференциальная числовая функция распределения выражает зависимость числовой доли макромолекул от их ММ. Дискретная дифференциальная массовая функция распределения выражает зависимость массовой доли макромолекул от ММ. Дискретные функции распределения обычно применяются при теоретических расчетах и выводах. При эксперименталь­ном изучении ММР обычно имеют дело с непрерывными кривыми и функ­циями распределения.

Значение непрерывной дифференциальной числовой функции распределе­ния f_n(M) равно числовой доле макромолекул с ММ от М до M+dM, делен­ной на dM; значение непрерывной массовой функции распределения f_w(M) равно массовой доле макромолекул с ММ от М до M+dM, деленной на dM.

Непрерывные дифференциальные числовые и массовые функции связаны между собой, как и соответствующие дискретные функции, простым соот­ношением:

. (1.7)

Помимо дифференциальных, широко используются интегральные функ­ции распределения:

значение (ордината) интегральной числовой функции распределения F_n(M) равно числовой доле макромолекул, имеющих ММ от минимальной до заданной М;

значение (ордината) интегральной массовой функции распределения F_n(M) равно массовой доле макромолекул, имеющих ММ от минимальной до заданной М.

Дискретные и непрерывные интегральные функции практически совпада­ют. Дифференциальные непрерывные функции могут быть получены из инте­гральных путем дифференцирования, наоборот - путем интегрирования.

Графической формой аналитической функции распределения является кривая ММР полимеров. На рис. 1.8 приведены дифференциальные кри­вые ММР, отвечающие рассмотренным выше непрерывным функциям. Кривые дифференциального распределения могут иметь один максимум, соответствующее распределение называется унимодальным, два или бо­лее максимумов, что отвечает полимодальному распределению, могут не иметь максимумов. Площади фигур, ограниченные кривыми дифферен­циального распределения и отрезком оси абсцисс, равны 1 или 100%, геометрический центр тяжести этих фигур (точки А, В) соответствует или (см. рис. 1.8). Интегральные кривые ММР имеют предельное значение ординаты, равной единице, т.е. F_n(M)→1, F_W(M) →1 при М→ (рис. 1.9).

Кривые дифференциального распределения могут быть построены из интегральных путем графического дифференцирования, и наоборот, инте­гральные кривые могут быть построены из дифференциальных путем гра­фического интегрирования. Первая задача решается в том случае, когда ММР полимеров изучается методами препаративного фракционирования – дробного осаждения или последовательного растворения. По полученным таким образом данным о количестве и ММ фракций полимеров строится интегральная кривая распределения, затем путем построения касательных к этой кривой - дифференциальная кривая распределения. В настоящее время препаративное фракционирование применяется лишь в тех случаях, когда необходимо получить узкие фракции полимеров для дальнейших исследо­ваний. Обычно применяются менее трудоемкие методы с автоматической записью дифференциальной кривой распределения, например гель-хромато­графия.

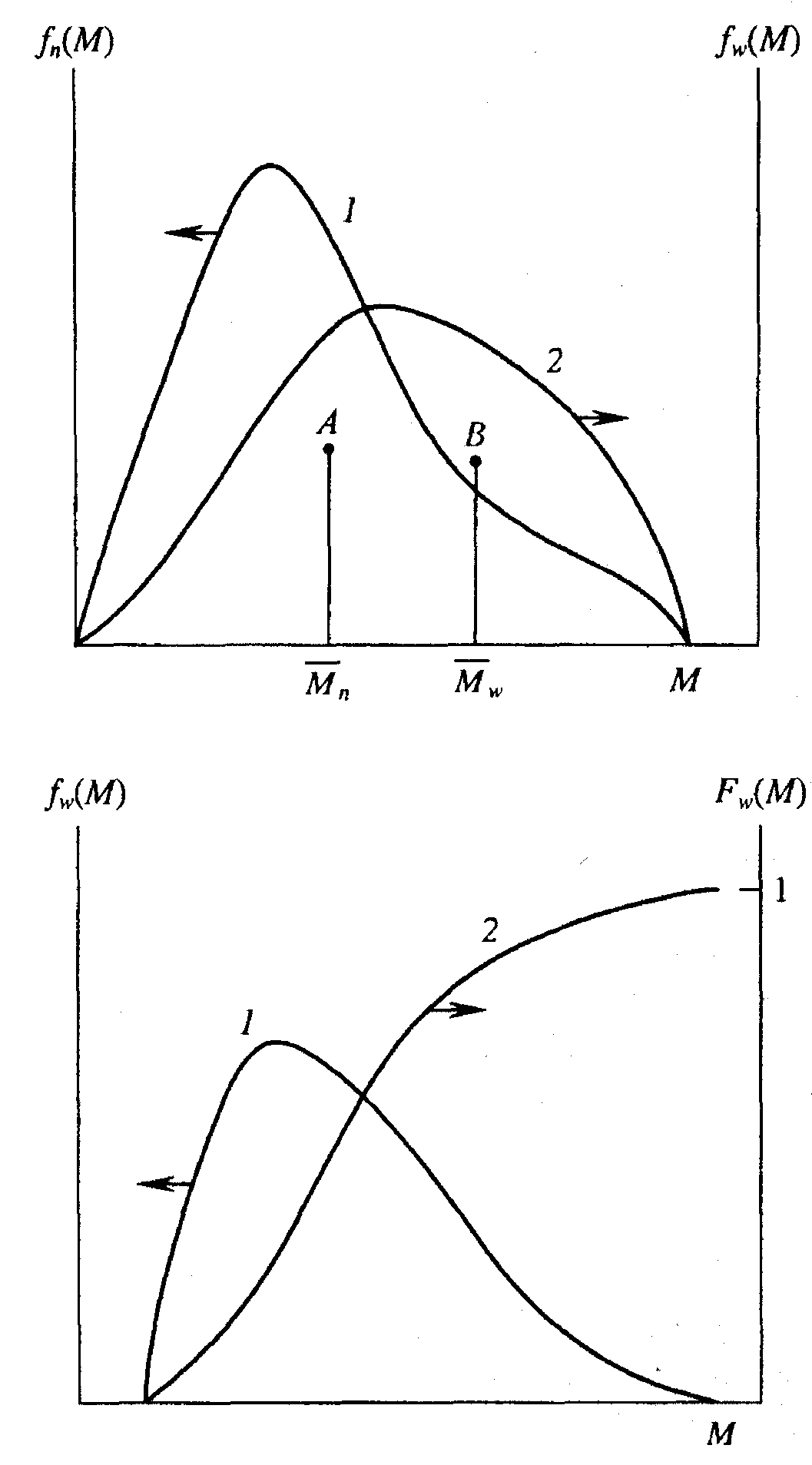
Рис. 1.8 Кривые числового (1) и массового (2) молекулярно-массовых распределений одно­го образца полимера

Рис. 1.9 Кривые дифференци­ального (1) и интегрального (2) молекулярно-массового распределения одного образца полимера