1.6.Регрессионный анализ

Для проведения регрессионного анализа имеется несколько десятков ППП в том числе ППП EXCEL’2003 и STATTISTICA 6.0. Между одинаковыми функциями этих двух пакетов есть некоторая разница: ППП EXCEL’2003 подходит для анализа небольших задач, включающих не более 16 независимых переменных (влияющих факторов), а STATISTICA 6.0 имеет верхний предел в 100 факторов. Несомненным достоинством ППП STATISTICA 6.0 по сравнению с EXCEL’2003 является наличие режима пошаговой регрессии, который позволяет оставлять в получаемых зависимостях только наиболее значимые факторы.

В этом разделе подробно рассмотрено использование ППП STATISTICA 6.0 как более предпочтительное средство регрессионного анализа. Для использования же регрессионного анализа в EXCEL’2003 необходимо воспользоваться пунктом меню «Сервис| Анализ данных| Регрессия» и далее следовать инструкциям EXCEL.

Надо отметить, что перед построением регрессионных моделей целесообразно сделать корреляционный анализ данных, который позволяет сделать заключение о целесообразности линейного регрессионного анализа. Для корреляционного и регрессионного анализа необходимо в переключателе модулей STATISICA 6.0 выбрать модуль <Multiple Regression> (Множественная Регрессия).

Для того, чтобы просмотреть средние значения величин и их стандартные отклонения, необходимо щелкнуть кнопку <Means & SD>. Матрицу значений коэффициентов линейной корреляции можно просмотреть, щелкнув по кнопке <Correlations>.

Матрица попарных коэффициентов линейной корреляции представляется в виде табл.1.6.1.:

Таблица 1.6.1. Табличная форма представления корреляционной матрицы

	х1	x2	х3	…	У1	У2
х1	1
х2	0,811096	1
х3	-0,22135	0,040212	1
…..				…….
У1	-0,64918	-0,64549	-0,09185		1
У2	-0,11858	0,213939	0,748497		-0,06477	1

Парные коэффициенты линейной корреляции принимают значения от -1 до +1. Значение, близкое к +1, указывает на наличие сильной положительной линейной зависимости между переменными. Значение, близкое к -1, указывает на наличие сильной отрицательной линейной зависимости между переменными. Значение, близкое к 0, указывает на слабую зависимость переменных друг от друга.

После анализа попарных коэффициентов линейной корреляции можно переходить непосредственно к регрессионному анализу. Линейную регрессию рассматривать не будем, так как она в целом схожа с процедурой пошаговой регрессии (ППР). Для выполнения ППР необходимо определение зависимостей показателей эффективности от влияющих на них факторов

,

(3)

где – количество показателей эффективности;

–количество влияющих факторов.

Для получения такой математической зависимости, т.е. определения числовых значений коэффициентов bij, используем концепцию "черного ящика", по которой, абстрагируясь от физической сущности процессов, происходящих в объекте исследования, будем судить о его поведении только по уровням значений независимых переменных, называемых факторами, и зависимыми переменными, называемыми откликами. Такой подход правомерен в условиях затруднения получения аналитических зависимостей междуy_iи совокупностью переменныхx_j,, что и имеет место в нашем случае.

Поставлена задача минимизации количества переменных, входящих в уравнение регрессии из совокупности заданных переменных.

, ,

(4)

где Q_j- число переменных в j-том уравнении регрессии;

U_ji - коэффициент, принимающий значение “1”, если i-ая переменная входит в j-ое уравнение регрессии и “0”, если не входит;

L - общее количество переменных, задаваемое для отбора, составленное из самих факторов, попарных произведений факторов между собой и различных функций от факторов;

k – количество уравнений регрессии.

На получаемые уравнения регрессии наложены следующие ограничения:

1. Уровень значимости коэффициента детерминации, показывающий в долях от единицы насколько изменение переменных, вошедших в уравнение регрессии, описывают изменение показателя эффективности, должен быть менее 0,05 , т.е.

   ,

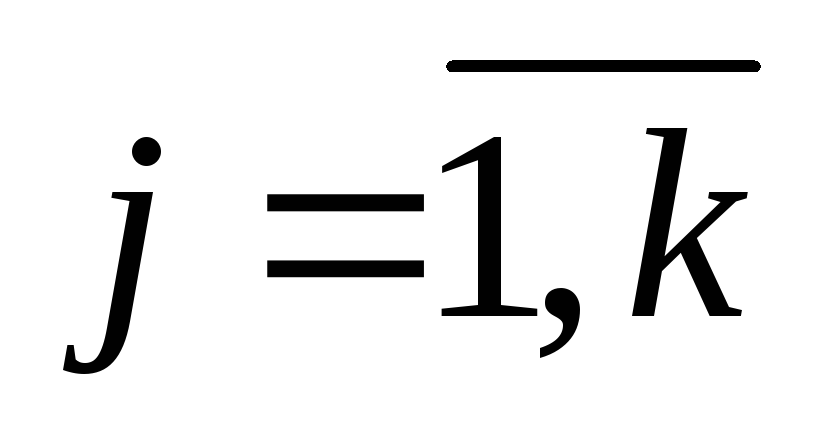
   (5)

2. Величина отношения среднеквадратической ошибки аппроксимации к среднему значению отклика не должна превышать 0,05 в долях от единицы, т.е.

   ,

   (6)

3. Уровень значимости уравнения регрессии по критерию Фишера должен быть не более 0,05

   ,

   (7)

4. Все коэффициенты уравнения регрессии должны иметь уровень значимости по критерию Стьюдента не более 0,05

, ,

(8)

В окне результатов регрессионного анализа (рис.1.6.1) представлены следующие сведения:

Dep. Var.: Y - зависимая переменная Y:

No. of cases: количество обработанных случаев ;

Multiple R: - коэффициент множественной корреляции;

R*: - коэффициент множественной детерминации;

adjusted R*: - скорректированный коэффициент множественной детерминации;

F - значение критерия Фишера;

df - количество степеней свободы;

p - уровень значимости уравнения регрессии по критерию Фишера;

Standard error of estimate: - стандартная ошибка аппроксимации;

Intercept: - значение свободного члена;

Std. Error: - стандартная ошибка свободного члена;

t( ) = значение критерия Стьюдента при количестве степеней свободы;

p -уровень значимости критерия Стьюдента;

Рис.1.6.1. Основные результаты регрессионного анализа

Под чертой в окне расположены стандартизированные коэффициенты при переменных, причем значимые коэффициенты выделены красным цветом. Подробнее результаты регрессии можно посмотреть, щелкнув по кнопке <Regression Summary> (рис.1.6.2).

Рис.1.6.2. Табличное представление уравнения регрессии

Первый столбец (рис.1.6.2) - это перечень факторов, вошедших в уравнение регрессии и свободный член <Intercept>, второй - стандартизированные коэффициенты BETA при них, далее идут стандартные ошибки для коэффициента BETA. В четвертом столбце - коэффициенты при факторах в уравнении регрессии В и их стандартные ошибки. В последнем столбце <p-level> уровни значимости коэффициентов уравнения регрессии по критерию Стьюдента.