4.1. Решение задачи нагрева в программном комплексе comsol Multiphysics(Femlab)

Пакет COMSOL Multiphysics позволяет моделировать практически все физические процессы, которые описываются частными дифференциальными уравнениями. Программа содержит различные решатели, которые помогут быстро справиться даже с самыми сложными задачами, а простая структура приложения обеспечивает простоту и гибкость использования. Решение любой задачи базируется на численном решении уравнений в частных производных методом конечных элементов. Спектр задач, которые поддаются моделированию в программе чрезвычайно широк.

Набор специальных модулей в программе охватывает практически все сферы приложений уравнений в частных производных.

COMSOL Multiphysics (Femlab) – пакет моделирования, который решает системы нелинейных дифференциальных уравнений в частных производных методом конечных элементов в одном, двух и трех измерениях. Он позволяет решать задачи из области электромагнетизма, теории упругости, динамики жидкостей и газов и химической газодинамики. Femlab также дает возможность решить задачу как в математической постановке (в виде системы уравнений), так и в физической (выбор физической модели, например модели процесса диффузии). Безусловно в любом случае будет решаться система уравнений, и различие заключается лишь в возможности использовать физические системы единиц и физическую терминологию. В так называемом физическом режиме работы также можно использовать заранее определенные уравнения для большинства явлений, имеющих место в науке и технике, таких как перенос тепла и электричества, теория упругости, диффузия, распространение волн и поток жидкости.

4.1.1. Нагрев тела при граничных условиях I рода с постоянными теплофизическими свойствами

Рассмотрим одномерную модель однослойной пластины толщиной 0,1 м с граничными условиями I рода с одной стороны и II рода (условия адиабаты) c другой. Температура внешней стороны пластины равна 1000 °С. Время нагрева пластины 1000 с.

НАВИГАТОР МОДЕЛЕЙ

Откройте Model Navigator.

Выберите в списке Space Dimension 1D.

В Application Mode выберите режим COMCOL Multiphysics > Heat Transfer > Conduction > Transient analysis.

Нажмите OK.

Откроется рабочая область с одной координатной осью.

ЗАДАНИЕ ГЕОМЕТРИИ

Выберите пункт меню Draw>Specify Objects>Line.

В открывшемся окне введите координаты пластины в поле Coordinates. 

Толщина пластины 10 см. Введите в поле цифры 0 0.1.

Нажмите OK. В рабочей области на оси х появится линия, названная по умолчанию I1.

Это же окно можно открыть, если щелкнуть на кнопке Line при нажатой клавише Shift.

Нажмите OK.

Нажмите кнопку Zoom Extents, для того чтобы расположить фигуру на весь экран.

ФИЗИЧЕСКИЕ УСТАНОВКИ

Свойства подобласти

Для задания физических свойств материала пластины требуется следующее.

Откройте окно Physics>Subdomain Settings… (в последней версии программы оно вызывается клавишей F8).

В Subdomain selection выберите номер пластины. В рабочей области эта область сразу выделится красным.

Введите в поля свойства для стали в соответствии с табл. 3.1.

В остальных полях оставьте нулевые значения.

Для того чтобы установить начальное значение температуры, откройте в том же окне вкладку Init.

Введите 273 как начальное значение в поле Temperature.

Нажмите OK.

Граничные условия

Откройте окно Physics > Boundary Settings… (F7).

В Boundary selection выберите номер границы. В рабочей области соответствующая граница выделяется красным.

Введите граничные условия в соответствии с табл. 4.1.1.

В нашем случае можно использовать линейный решатель, так как все физические свойства и коэффициенты приняты не зависящими от температуры.

Нажмите OK.

Таблица 4.1.1. Граничные условия

№ границы	Граница	Вид ГУ	Коэффициенты ГУ
1	Среда–сталь	Temperature	T0=1273 К
2	Сталь–среда	Thermal insulation

ГЕНЕРАЦИЯ СЕТКИ

После задания всех граничных условий определите сетку командой Mesh > Initialize Mesh или кнопкой . Получится пятнадцать узлов по длине стенки. Чтобы увеличить количество узлов, надо нажать кнопку(Mesh > Refine Mesh). При необходимости её можно нажать несколько раз.

РАСЧЕТ

В меню Solve (Решать) выберите Solver Parameters (Параметры решателя).

В списке Solver (Решатель) выберите Time dependent (Зависимый от времени).

На вкладке General в первом поле Times вместо 0:0.1:1 введите 0:20:1000. Это значит, что для вывода решения будет использоваться шаг по времени 20 секунд. Этот шаг не имеет отношения к точности решения, но для визуализации он важен. В самом решателе шаг по времени достаточно маленький и зависит от скорости изменения температуры. Расчет будет длиться до 1000 с.

Нажмите OK.

Нажмите кнопку Solve (Решать). (Solve > Solve Problem). Получите распределение температуры по толщине пластины в основном окне.

ВИЗУАЛИЗАЦИЯ

После работы решателя в главном окне будет выведено распределение температур по толщине пластины (рис. 4.1.1).

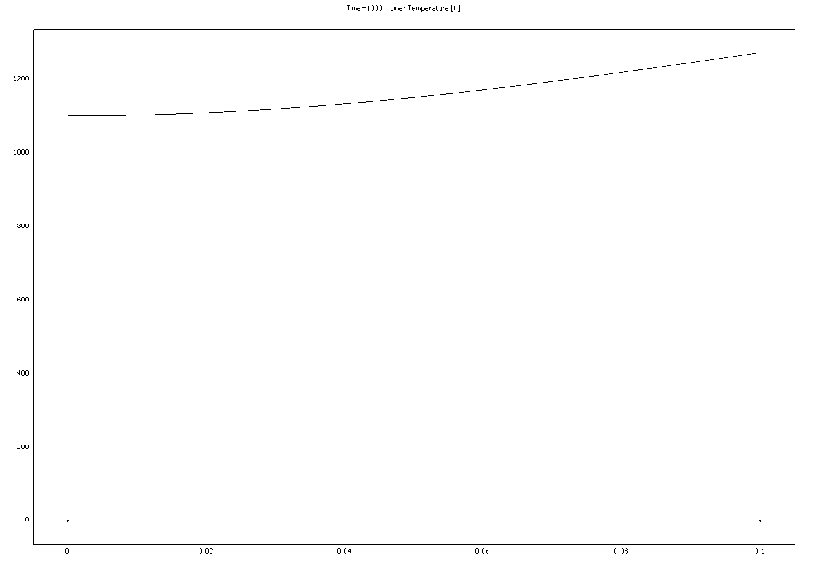
Рис. 4.1.1. Распределение температуры по толщине пластины

По результатам расчета видно, что при условиях нестационарного режима температура теплового центра пластины равна 1099,9 К.