
- •О.Ю. Нагорная инженерный анализ теплового оборудования
- •Введение
- •1. Инженерный анализ теплового оборудования средствами компьютерного моделирования
- •1.1. Анализ тепловых явлений
- •2. Аппроксимация теплофизических свойств материала от температуры
- •2.1. Определение зависимости коэффициента теплопроводности от температуры
- •2.2. Определение зависимости удельной теплоемкости от температуры
- •2.3. Определение зависимости плотности от температуры
- •2.4. Определение зависимости коэффициента температуропроводности от температуры
- •3. Решение задачи нагрева металла аналитическим методом
- •3.1. Постановка задачи (постоянные теплофизические свойства)
- •3.1.1. Решение задачи нагрева металла с постоянными теплофизическими свойствами аналитическим методом в среде MathCad
- •3.2. Постановка задачи (переменные теплофизические свойства)
- •3.2.1. Решение задачи нагрева металла с переменными теплофизическими свойствами аналитическим методом в среде MathCad
- •4. Решение задач нагрева металла в различных многоцелевых вычислительных комплексах
- •4.1. Решение задачи нагрева в программном комплексе comsol Multiphysics(Femlab)
- •4.1.1. Нагрев тела при граничных условиях I рода с постоянными теплофизическими свойствами
- •4.1.2. Нагрев тела при граничных условиях I рода с учётом зависимости теплофизических свойств от температуры
- •4.2. Решение задач нагрева в программном комплексе Elcut
- •4.2.1. Нагрев тела при граничных условиях I рода с постоянными теплофизическими свойствами
- •4.2.2. Нагрев тела при граничных условиях I рода с переменными теплофизическими свойствами
- •4.3. Решение задач нагрева в программном комплексе FlowVision
- •4.3.1. Нагрев тела при граничных условиях I рода с постоянными теплофизическими свойствами
- •4.3.2. Нагрев тела при граничных условиях I рода с учётом зависимости теплофизических свойств от температуры
- •4.4. Решение задач нагрева в многофункциональном программном комплексе конечно-элементных расчетов ansys
- •4.4.1. Нагрев тела при граничных условиях I рода с постоянными теплофизическими свойствами
- •4.4.2. Нагрев тела при граничных условиях I рода с учётом зависимости теплофизических свойств от температуры
- •4.4.2.1. Создание пользовательской базы данных
- •4.4.2.2. Задание переменных свойств материала с помощью кусочно-линейной функции
- •4.4.2.3. Задание переменных свойств материала с помощью полиномиальной функции
- •4.4.2.4. Задание переменных свойств материала с помощью кусочно-полиномиальной функции
- •4.4.2.5. Анализ способов задания переменных свойств материала
- •5. Моделирование воздушно-водяного кожухотрубчатого теплообменника типа «труба в трубе»
- •5.9. Окно создания и редактирования материалов
- •5.10. Выбор необходимого материала (жидкости)
- •Библиографический список
- •Приложение 2
2.2. Определение зависимости удельной теплоемкости от температуры
Построение точечной диаграммы и вывод уравнений производится аналогично п. 2.1 (рис. 2.12).
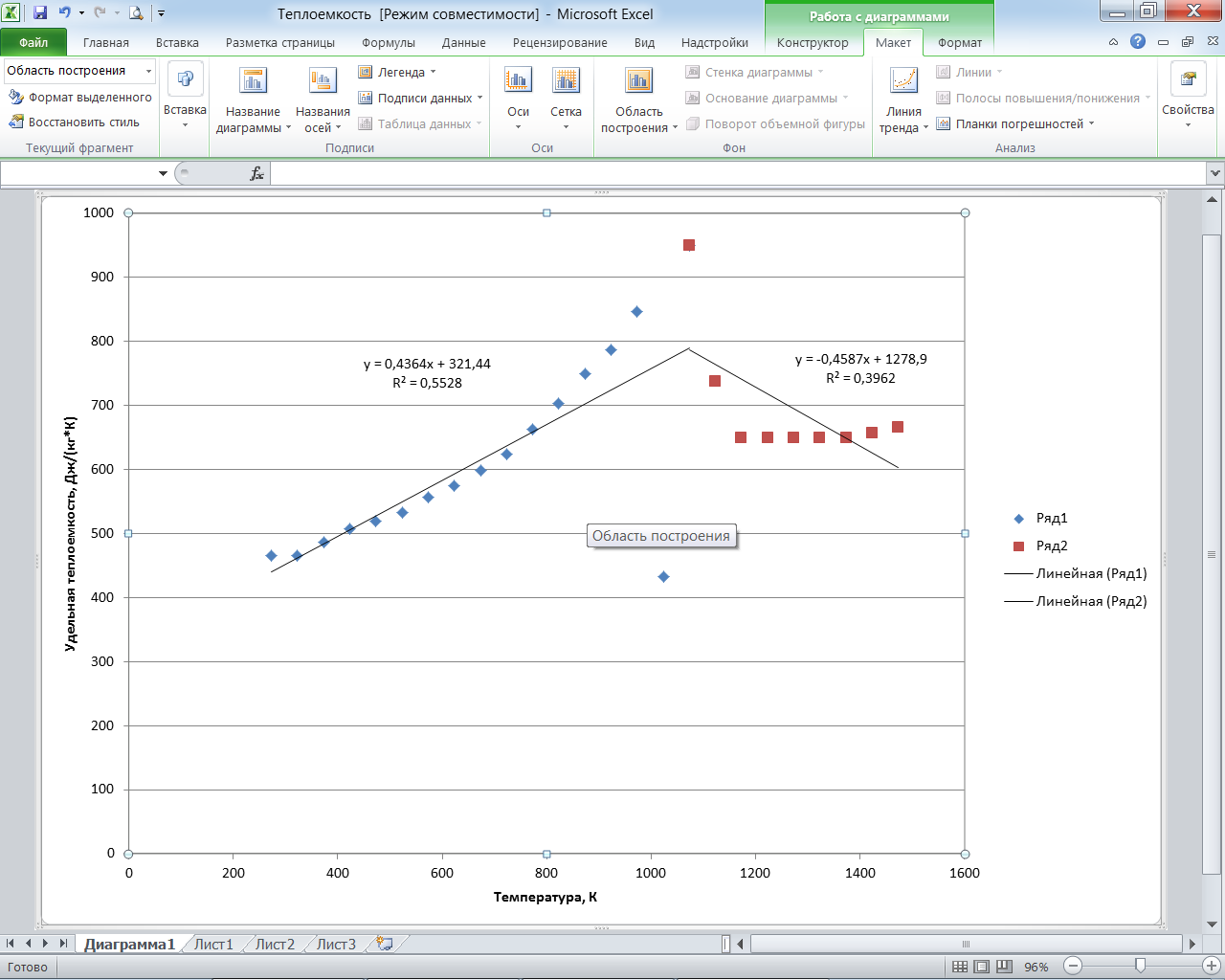
Рис. 2.11. Диаграмма с линиями тренда и уравнениями, определяющими зависимость удельной теплоемксоти от температуры
В итоге получаем, что в диапазоне температур от 273 К до 1073 К изменение коэффициента удельной теплоемкости для стали 20 описывается уравнением с(Т) = 321,44+0,4364∙Т Дж/(кг∙К), а в диапазоне от 1073 К до 1473 К уравнением с(Т) = 1278,9-0,4587∙Т Дж/(кг∙К).
2.3. Определение зависимости плотности от температуры
Построение точечной диаграммы и вывод уравнений производится аналогично п. 2.1 (рис. 2.12).
В итоге получаем, что в диапазоне температур от 273 К до 1473 К изменение плотности для стали 20 описывается уравнением ρ(Т) = 7948,2-0,3158∙Т кг/м3.
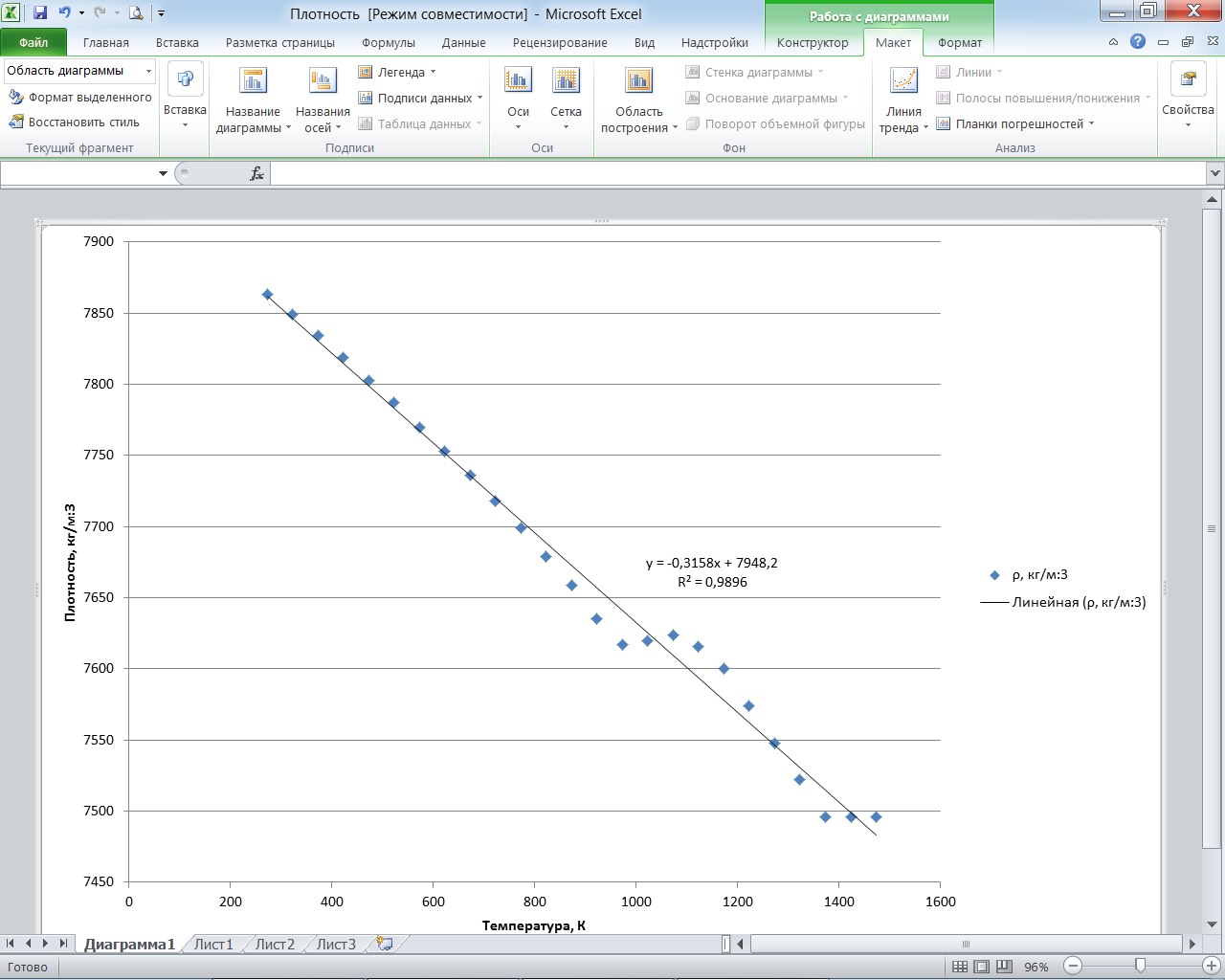
Рис. 2.12. Диаграмма с линией тренда и уравнением, определяющими зависимость плотности от температуры
2.4. Определение зависимости коэффициента температуропроводности от температуры
Построение точечной диаграммы и вывод уравнений производится аналогично п. 2.1 (рис. 2.13).
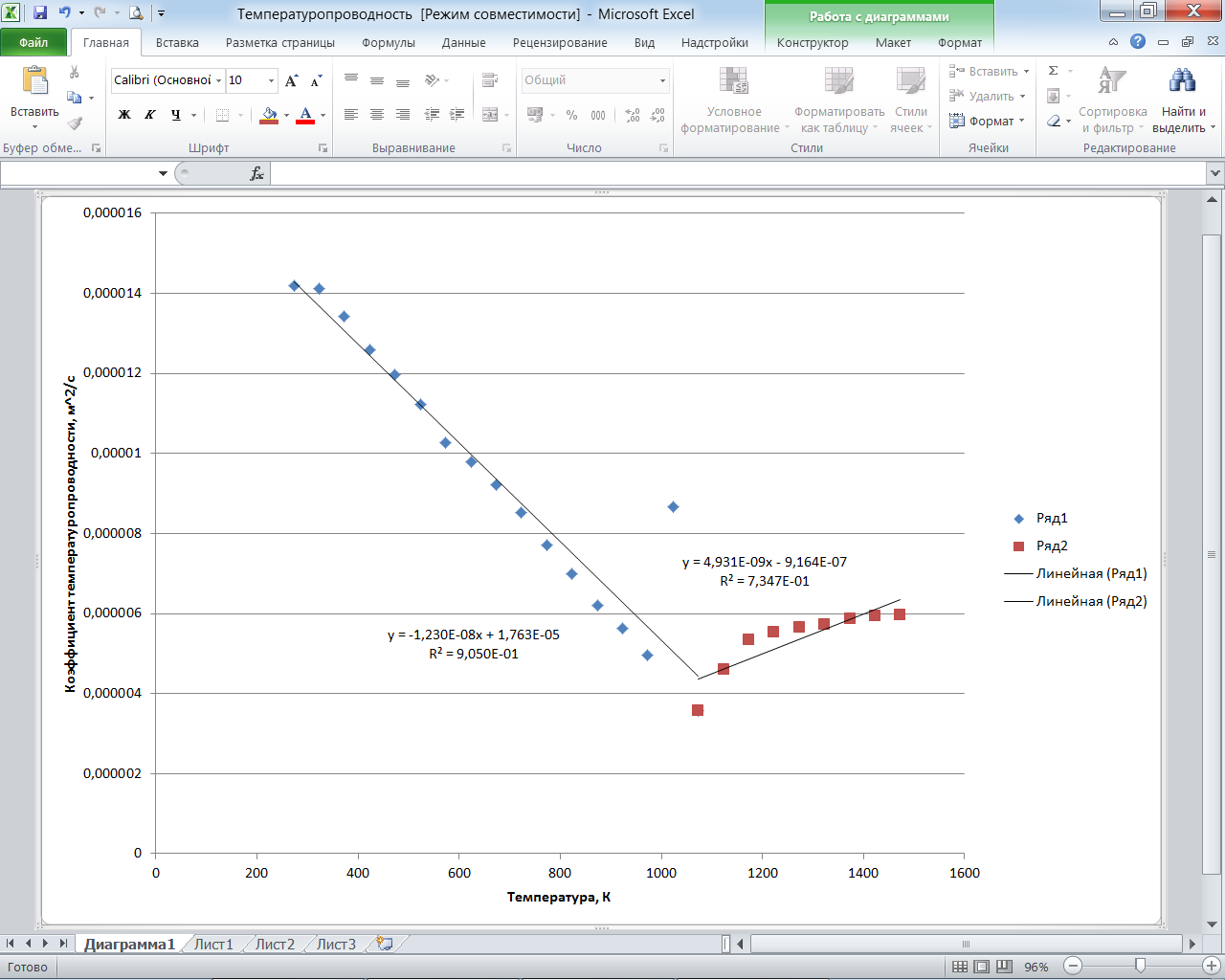
Рис. 2.13. Диаграмма с линиями тренда и уравнениями, определяющими зависимость коэффициента температуропроводности от температуры
В итоге получаем, что в диапазоне температур от 273 К до 1073 К изменение кооэффициента температуропроводнсти для стали 20 описывается уравнением а(Т) = 1,763Е-05-1,230Е-08∙Т м2/с, а в диапазоне от 1073 К до 1473 К уравнением а(Т) = -9,164Е-07+4,931Е-09∙Т м2/с.
3. Решение задачи нагрева металла аналитическим методом
Цель работы: необходимо решить дифференциальное уравнение теплопроводности аналитическим методом с учетом постоянных и переменных теплофизических свойств материала, найти распределение температуры по толщине пластины в любой момент времени.
3.1. Постановка задачи (постоянные теплофизические свойства)
Дана неограниченная пластина толщиной 0,1 м с начальной температурой 273 К. К поверхности пластины приложен источник с постоянной температурой 1273 К, а на нижней границе заданы адиабатические условия нагрева. Время нагрева составляет 1000 секунд.
Условие задачи математически может быть сформулировано следующим образом.
Для металла прирост теплосодержания будет происходить только за счёт теплопроводности, то есть уравнение теплопроводности будет иметь вид:
 ,
,
где
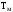 – температура металла, К;
– температура металла, К;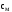 – удельная
теплоёмкость металла,
– удельная
теплоёмкость металла,
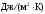 ;
;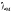 –
теплопроводность материала металла,
–
теплопроводность материала металла,
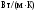 ;
;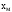 – текущая
пространственная координата металла,
– текущая
пространственная координата металла,
 ;
; – время, с.
– время, с.
Начальные условия:
 К, где 0 < xм
≤ 0,1 м.
К, где 0 < xм
≤ 0,1 м.
Граничные условия:
1 рода на одной поверхности металла:
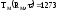 ,
0 < τ
≤ τк.
,
0 < τ
≤ τк.
2 рода на другой поверхности металла:
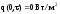 ,
0 < τ
≤ τк.
,
0 < τ
≤ τк.
3.1.1. Решение задачи нагрева металла с постоянными теплофизическими свойствами аналитическим методом в среде MathCad
Решение задачи аналитическим методом осуществляется в математической среде MathCAD, где с помощью встроенных функций и команд имеется возможность решения дифференциальных уравнений. Зная основное ДУ теплопроводности, можно легко получить аналитическую зависимость изменения температуры и количества переданного тепла во времени для любой точки тела.
Сначала надо описать постоянные величины:
τ = 1000 – время расчета или нагрева пластины, с;
r = 0,1 – толщина пластины, м;
c
– удельная массовая теплоемкость стали,
 ;
;
ρ – плотность стали, кг/м3;
λ – коэффициент
теплопроводности,
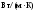 .
.
Для стали 20 средние
для диапазона температур 0 14730С
теплофизические свойства представлены
в таблице 3.1.
14730С
теплофизические свойства представлены
в таблице 3.1.
Таблица 3.1. Свойства материала
|
Теплопроводность λ , Вт/(м·К) |
Плотность ρ, кг/м3 |
Теплоёмкость С, Дж/(кг·К) |
|
38.67 |
7850 |
608.3 |
Затем записывается ДУ теплопроводности с начальными и граничными условиями, в виде указанном в постановке задачи. Записываются границы решения, и количество шагов по времени и по пространству, используя функцию pdesolve, которая как раз и является функцией решения дифференциальных уравнений в среде MathCAD.
Встроенная функция pdesolve применяется в рамках вычислительного блока, начинающегося ключевым словом Given, и пригодна для решения различных гиперболических и параболических уравнений. Она предназначена для решения одномерного уравнения (или системы уравнений) в частных производных (того, которое определит пользователь в рамках вычислительного блока Given), зависящего от времени t и пространственной координаты х, имеет целый набор различных аргументов и работает следующим образом: Pdesolve(u,x,xrange,t,trange,[xpts], [tpts]) – возвращает скалярную (для единственного исходного уравнения) или векторную (для системы уравнений) функцию двух аргументов (x,t), являющуюся решением дифференциального уравнения (или системы уравнений) в частных производных. Результирующая функция получается интерполяцией сеточной функции, вычисляемой согласно разностной схеме:
u – явно заданный вектор имен функций (без указания имен аргументов), подлежащих вычислению. Эти функции, а также граничные условия (в форме Дирихле или Неймана) должны быть определены пользователем перед применением функции pdesolve в вычислительном блоке после ключевого слова Given. Если решается не система уравнений в частных производных, а единственное уравнение, то, соответственно, вектор и должен содержать только одно имя функции и вырождается в скаляр;
х – пространственная координата (имя аргумента неизвестной функции);
xrange – пространственный интервал, т. е. вектор значений аргумента х для граничных условий. Этот вектор должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала);
t – время (имя аргумента неизвестной функции);
t range – расчетная временная область: вектор значений аргумента t, который должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала по времени);
xpts – количество пространственных точек дискретизации (может не указываться явно, в таком случае будет подобрано программой автоматически);
tpts – количество временных слоев, т. е. интервалов дискретизации по времени (также может не указываться пользователем явно).
Результаты решения приведены в табл. 3.2, а также получены в виде зависимостей, изображенных на рис. 3.1. Листинг программы в MathCAD приведен в приложении 2.
Таблица 3.2. Результаты решения задачи
|
τ, сек |
T(0, τ), оС |
|
200 |
430,83 |
|
400 |
700,79 |
|
600 |
889,09 |
|
800 |
1015,56 |
|
1000 |
1100,37 |

Рис. 3.1. График зависимости температур от времени нагрева
