Семинар 11

Кривые второго порядка на плоскости.

Вводная информация

Уравнение линии на плоскости.

Определение. Уравнением линии (кривой) на плоскости в декартовой системе координат называется уравнение , где - функция двух переменных и . В полярной системе координат уравнение линии имеет вид . Если уравнение разрешимо относительно переменной , то уравнение линии можно записать в виде .

Так как координаты точки, находящейся на линии связаны уравнением, то линия является одномерным геометрическим объектом. Задача о нахождении точек пересечения двух линий, заданных уравнениями и ,

сводится к решению системы двух уравнений с двумя неизвестными:

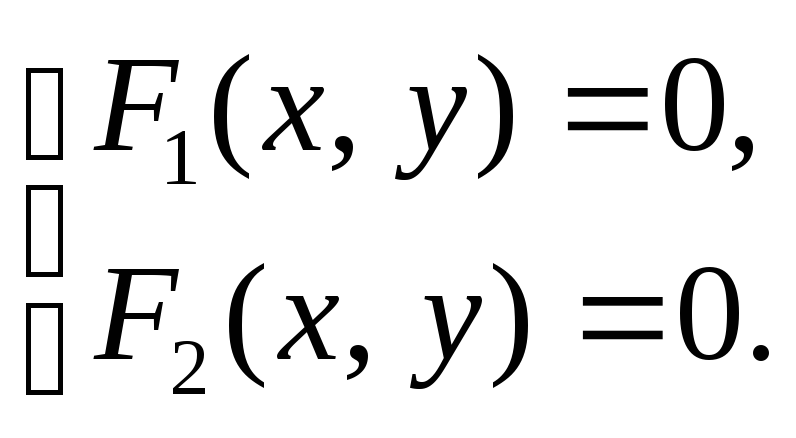
Линию на плоскости можно также задать параметрическим образом с помощью двух уравнений

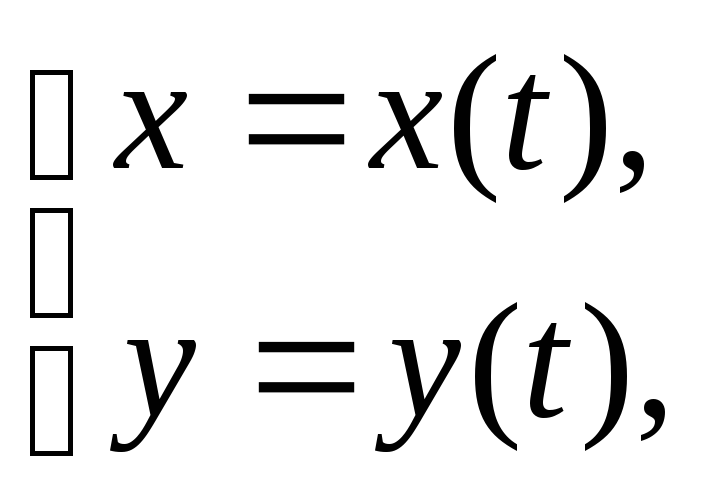
где и - координаты точки, лежащей на линии, а - переменная, называемая параметром.

Приведем примеры некоторых линий.

1. окружность радиуса 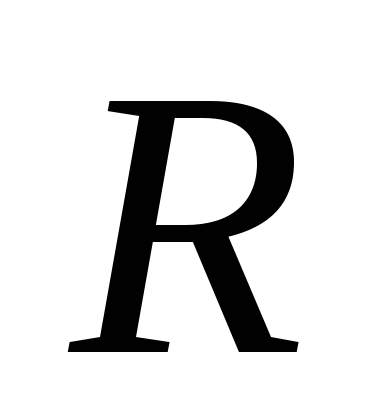с центром в начале координат.

Уравнения такой окружности имеют вид:

а) - в декартовой системе координат;

б) - в полярной системе координат;

в) 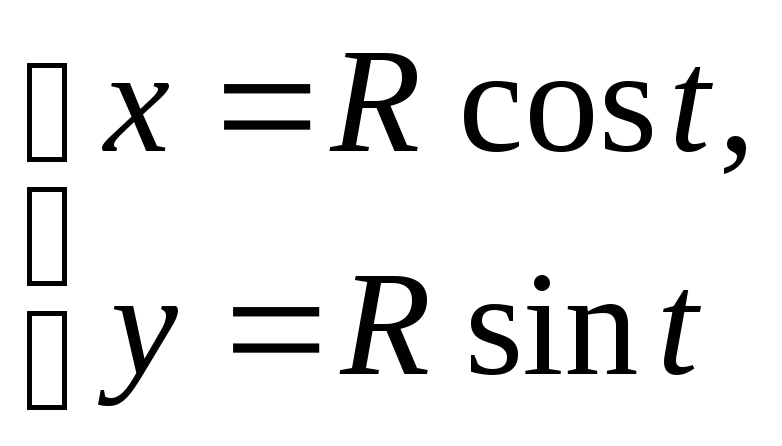- в параметрическом виде.

2) циклоида.

В параметрическом виде уравнение циклоиды имеет вид

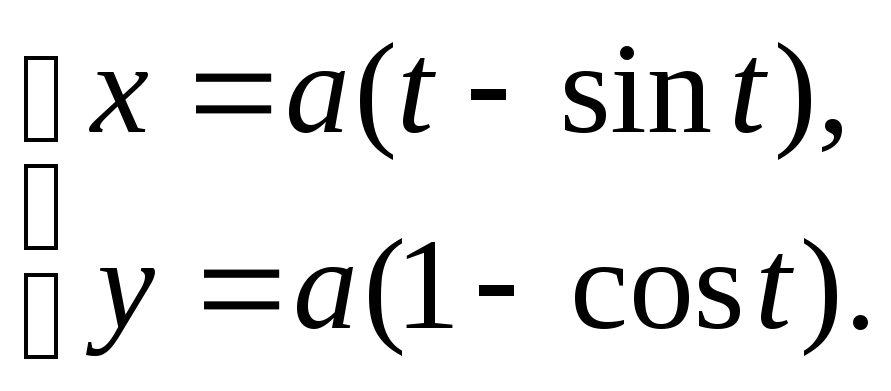
Такую кривую описывает точка на окружности радиуса , которая катится без скольжения по неподвижной прямой.

3. Астроида.

Астроида задается уравнениями:

а) - в декартовой системе координат;

б) 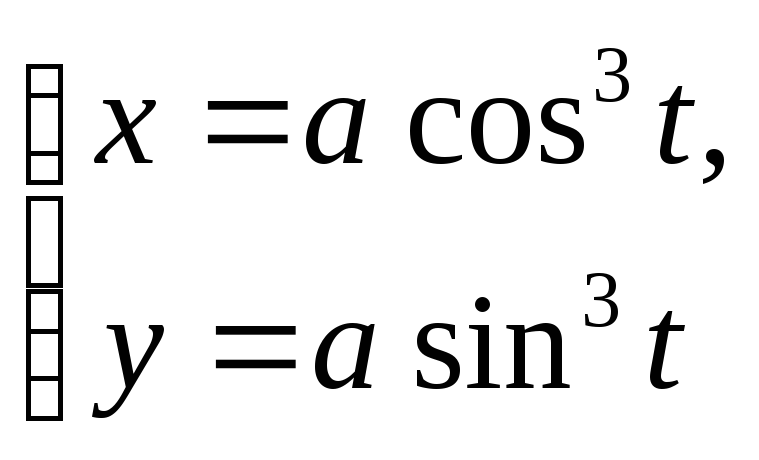- в параметрическом виде.

Такую кривую описывает точка на окружности радиуса , которая катится без скольжения по внутренней стороне окружности радиуса .

3. кардиоида.

Уравнение кардиоиды в полярной системе координат имеет вид

.

Эту кривую описывает точка окружности радиуса , катящаяся по окружности такого же радиуса с внешней стороны.

3. улитка Паскаля.

Уравнение кардиоиды является частным случаем () уравнения улитки Паскаля .

3. лемниската Бернулли.

Лемниската Бернулли задается уравнениями:

а) - в декартовой системе координат;

б) - в полярной системе координат.

Произведение расстояний каждой точки лемнискаты Бернулли до двух данных точек и равно квадрату расстояния между точками и .

7) декартов лист.

Декартов лист задается уравнениями:

а) - в декартовой системе координат;

б) 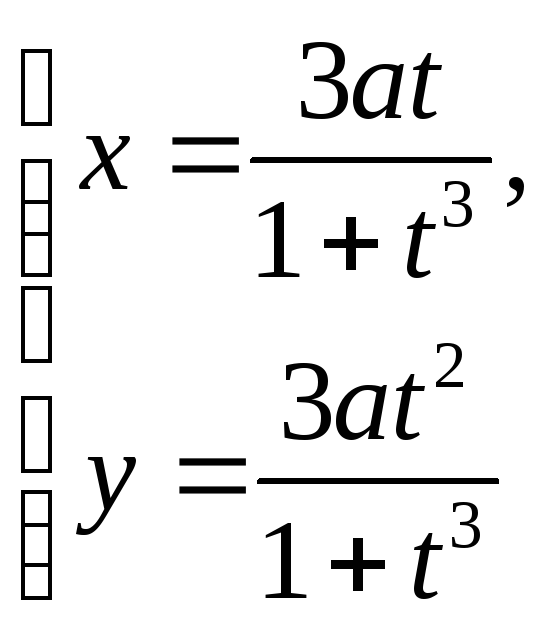- в параметрическом виде.

8) эвольвента (развертка) окружности.

В параметрическом виде эта кривая задается уравнениями

9) трехлепестковая роза.

В полярной системе координат эта кривая задается уравнением

10) четырехлепестковая роза.

Ее уравнение имеет вид .

11) спираль Архимеда.

Эта кривая в полярной системе координат описывается уравнением

12) логарифмическая спираль.

Ее уравнение имеет вид

13) гиперболическая спираль.

Эта кривая задается уравнением вида

Общее уравнение кривой второго порядка и приведение его к каноническому виду.

Общее уравнение линии второго порядка имеет вид

. (1)

При этом считается, что . В таком общем виде трудно понять, с какой кривой мы имеем дело. Поэтому при исследовании кривой, заданной этим уравнением, следует, вначале, привести данное уравнение с помощью координатных преобразований к каноническому (простейшему) виду.

1. Параллельный перенос начала координат.

Новую (штрихованную) систему координат введем с помощью соотношений

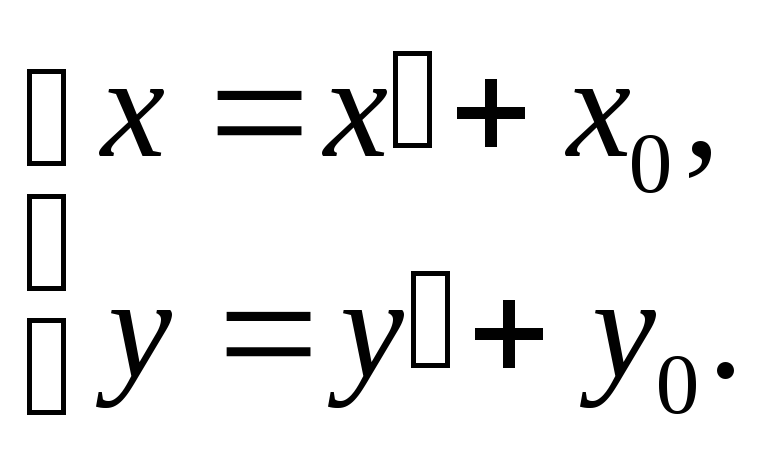
В новой системе координат уравнение (1) принимает вид

Выбирая в качестве постоянных величин и решение системы уравнений

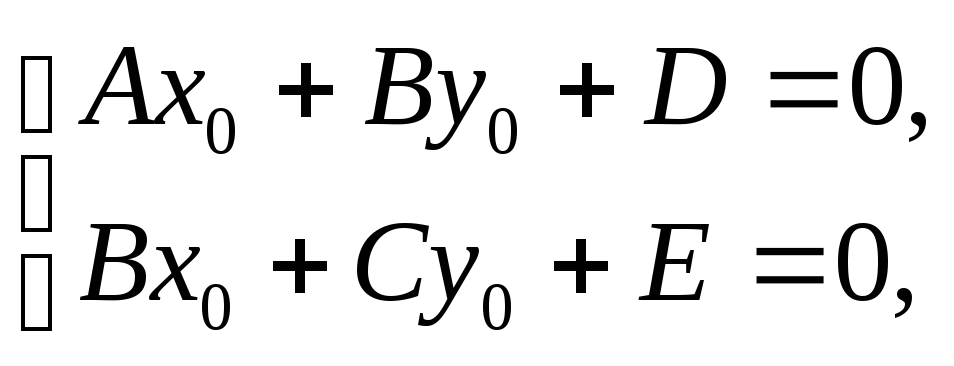(2)

мы можем исключить из уравнения кривой слагаемые с первой степенью переменных и . Таким образом, в декартовой системе координат с новым центром уравнение кривой второго порядка будет иметь вид

(3)

где .

При решении системы уравнений (2) возможны случаи:

1) . Система имеет единственное решение, точка называется центром кривой, а сама кривая называется центральной кривой. Центральными кривыми являются

а) - эллипсы;

б) - гиперболы.

2) . Возможны случаи:

а) система уравнений не имеет решения, кривые не имеют центра и называются параболами;

б) система уравнений имеет бесконечное множество решений, кривая называется вырожденной параболой (пара параллельных прямых или мнимое место точек).

Далее рассмотрим подробней случай центральных кривых. Сделаем поворот координатных осей на угол вокруг центра

Уравнение кривой (3) примет вид

,

где

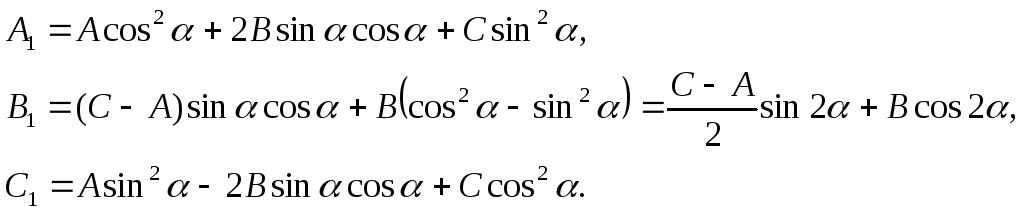
Выберем угол поворота координатных осей , удовлетворяющий равенству

или, что эквивалентно, равенству . Такой угол поворота выбирается из условия . Следовательно, уравнение кривой в системе координат примет канонический вид

. (1)

Пример 1. Приведем к каноническому виду уравнение кривой второго порядка, для которой . Найдем координаты центра кривой из системы уравнений

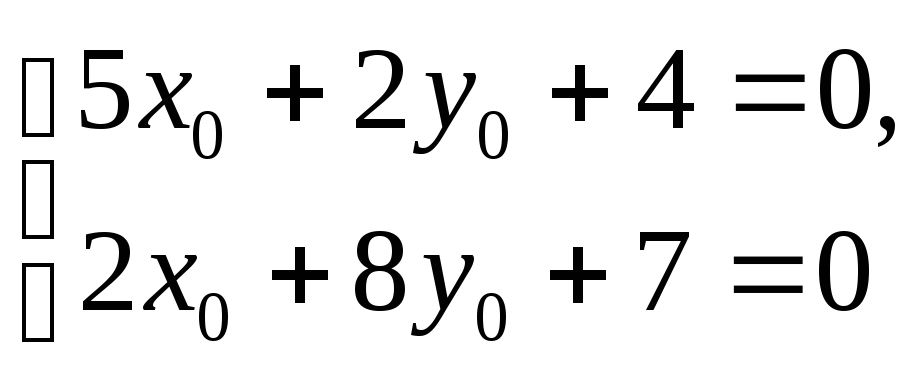
. В штрихованной системе координат уравнение кривой примет вид

.

Заметим, что для рассматриваемой кривой , т.е. кривая является эллипсом. Повернем координатные оси на угол , который найдем из уравнения . Это уравнение имеет два решения: . Поскольку , полученные два решения соответствуют двум взаимно перпендикулярным направлениям. Поэтому, замена одного угла на другой приводит только к замене оси на ось (или наоборот). Остановимся на первом решении . Учитывая, что и , находим и , а также коэффициенты и . Напомним, что нахождение угла поворота координатных осей осуществлялось из равенства . Таким образом, уравнение кривой в новой системе координат приобретает вид

.

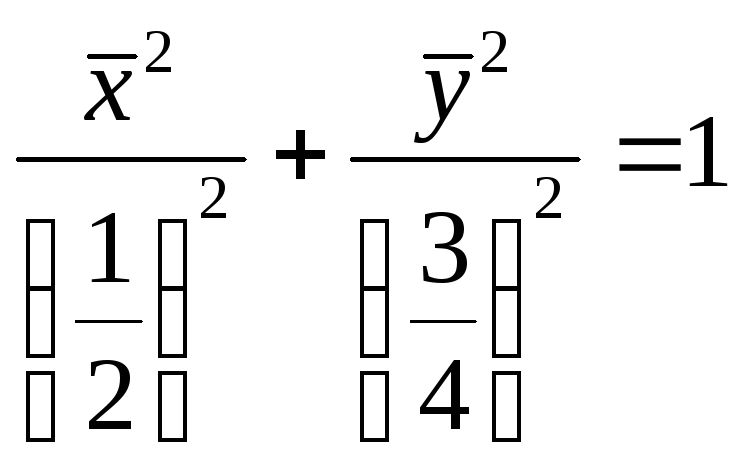Мы получили каноническое уравнение эллипса с полуосями .

Канонические уравнения окружности, эллипса, гиперболы и параболы.