Семинар 3

Числовые множества, группы и поля.

Вводная информация

Числовые множества

Определение. Скажем, что на множестве определенабинарная операция (закон композиции), если всяким двум элементам (различным или одинаковым) множества , взятым в определенном порядке, ставится в соответствие вполне определенный элемент этого же множества, т.е. бинарная операция – это отображение.

Число – основное понятие математики, сложившееся в ходе ее длительного развития. Практическая деятельность человека с одной стороны, внутренняя потребность математики – с другой стороны определили формирование этого понятия.

I. Множество натуральных чисел.

Потребность счета привела к возникновению понятия натурального числа. На множестве натуральных чисел определены две бинарные операции: сложение () иумножение (или просто). Обе эти операции коммутативны () и ассоциативны (,).

II. Множество целых чисел.

Проведение математических расчетов с натуральными числами потребовало расширения этого множества. К нему были добавлены новые элементы «0» и «-n», которые обладали свойствами: и. Ноль и элементы вида «-n» - отрицательные числа долгое время не считались числами, равноправными натуральным числам. Но математическая практика доказала необходимость их введения, что привело к формированию множества целых чисел , на котором введены те же две бинарные операции сложения и умножения. Сложение с отрицательным числом стали называть вычитанием.

III. Множество рациональных чисел.

Понятие рационального числа основано на понятии простой (обыкновенной) дроби , где. На множестве простых дробей также введены две бинарные операции правилами:и.

Рассмотрим две дроби и, для которых выполняется равенство.

Дроби, которые удовлетворяют этому равенству, назовем эквивалентными дробями и будем писать . Введенное отношение будет отношением эквивалентности. Действительно, имеют место

1. рефлексивность: ;

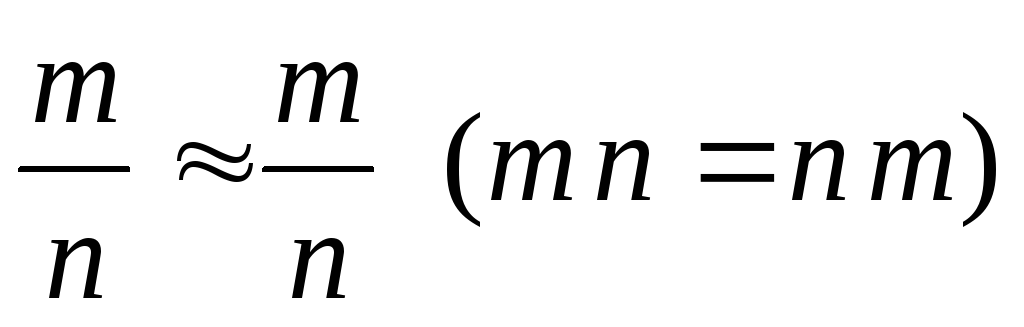2. симметрия: если 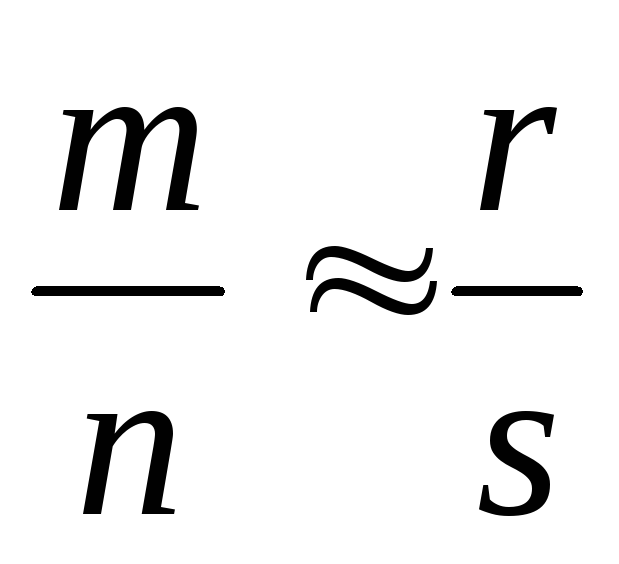, то();

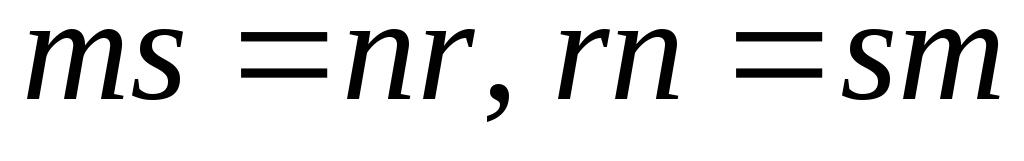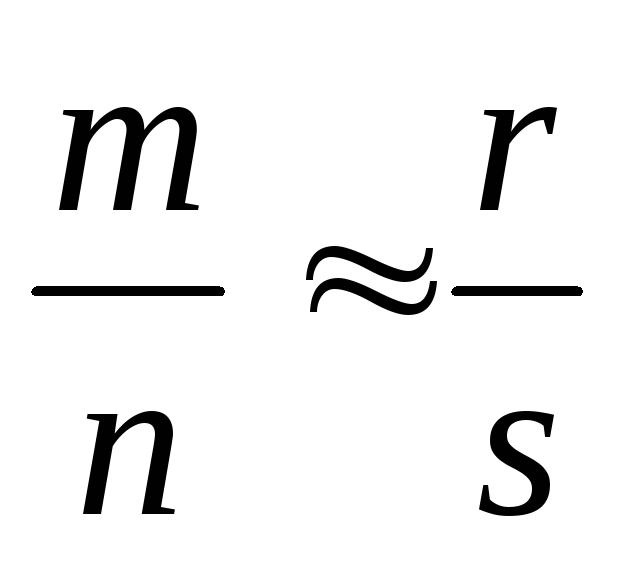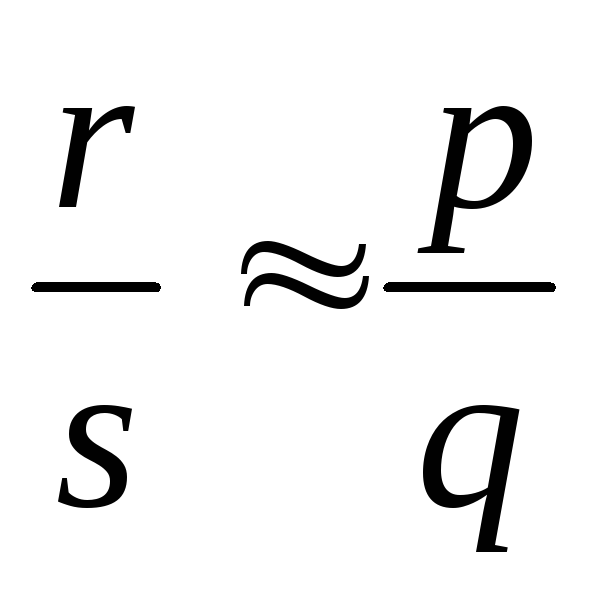3. транзитивность: если и, то.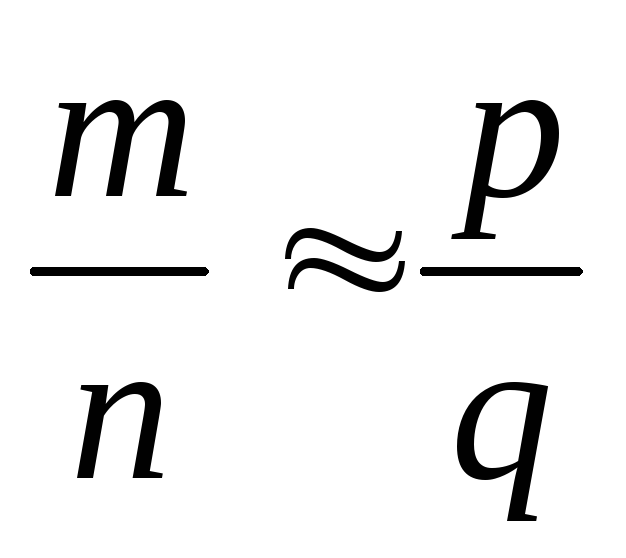

Введенное отношение эквивалентности позволяет разбить множество обыкновенных дробей на взаимно непересекающиеся классы.Рациональным числом будем называть класс всех эквивалентных дробей. При работе с рациональными числами можно взять любого представителя из класса, соответствующего данному рациональному числу (например, или, илии т. д.). При проведении вычислений с рациональными числами наиболее удобно брать дроби, гдеивзаимно простые числа. Такую запись рационального числа будем называть записью в виде несократимой дроби.

IV. Действительные числа.

Действительным числом называется бесконечная десятичная дробь вида

,

где из двух знаков «» берется какой-либо один: плюс – для положительных чисел (обычно не пишется), минус – для отрицательных чисел. Здесь- некоторое натуральное число или ноль, а- одна из цифр.

Рациональные числа задаются десятичными дробями с повторяющимися цифрами или конечными десятичными дробями.

Пример 1. а) -чистая периодическая дробь;

б) -смешанная периодическая дробь;

в) (ноль в периоде обычно отбрасывают).

Бесконечные десятичные дроби с неповторяющимися числами называются иррациональными числами.

Пример 2. а) ;

б) .

На множестве действительных чисел также вводятся две бинарные операции: сложение и умножение. Очевидно,. На множестве действительных чисел также введеноотношение порядка.

А) Два числа иназываются равными, если они имеют одинаковые знаки и справедливы равенства.

Б) Если и- положительные неравные числа, тоили же при невыполнении этого неравенства существует такое натуральное число,

что () и. Будем считать, что, еслиили же.

В) Если - положительное число,- отрицательное число, положим.

С) Если и- отрицательные числа, будем считать, чтопри условии, ипри условии.

Целою частью числаназывается наибольшее целое число, меньшее.

Дробной частью числаназывается разность.

Теорема 1. Для любых двух вещественных чисел инайдется рациональное числотакое, что.

Теорема 2. Для любых двух вещественных чисел инайдется иррациональное числотакое, что.

Следовательно, между двумя любыми не равными друг другу действительными числами можно вставить бесконечное число как рациональных, так и иррациональных чисел. Множество являетсявсюду плотным множеством.

Пусть - непустое подмножество.

Определение. Множество называетсяограниченным сверху (снизу), если существует число такое, чтовыполняется неравенство. Числоназываетсяверхней гранью множества , а- егонижней гранью.

Определение. Число называетсяточной верхней гранью ограниченного сверху множества , если: 1); 2).

Определение. Число называетсяточной нижней гранью ограниченного снизу множества , если: 1); 2).

Точная верхняя грань обозначается , нижняя -.

Определение. Элемент называетсянаибольшим или максимальным (наименьшим или минимальным) элементом множества , если(). Эти числа соответственно обозначаютсяи. Согласно данным определениям точная верхняя грань множества– его наименьшая верхняя грань, точная нижняя грань множества– его наибольшая верхняя грань.

Определение. Множество называетсяограниченным, если оно ограничено сверху и снизу.

Если множество не ограничено сверху (снизу), то пишут.

Группы