
СЕМИНАР 4
.docСЕМИНАР 4
Комплексные числа, геометрическое изображение комплексных чисел, формы записи комплексных чисел, действия над комплексными числами.
Вводная информация
Определение комплексного числа.
Рассмотрим
множество пар
![]() .
Введем на этом множестве две бинарные
операции:
.
Введем на этом множестве две бинарные
операции:
-
Сложение:
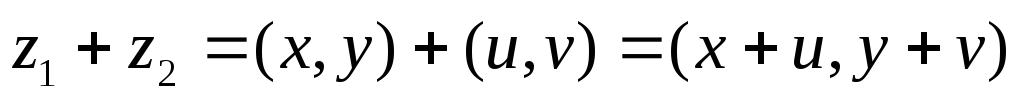 .
Относительно этой бинарной операции
множество
.
Относительно этой бинарной операции
множество
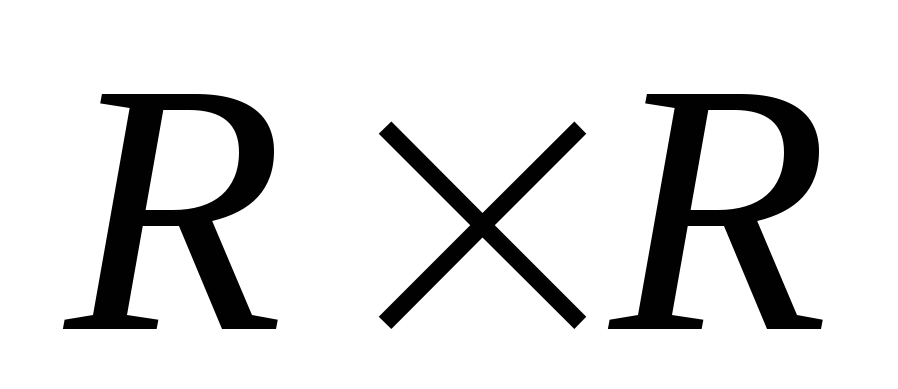 является абелевой группой с единичным
элементом
является абелевой группой с единичным
элементом
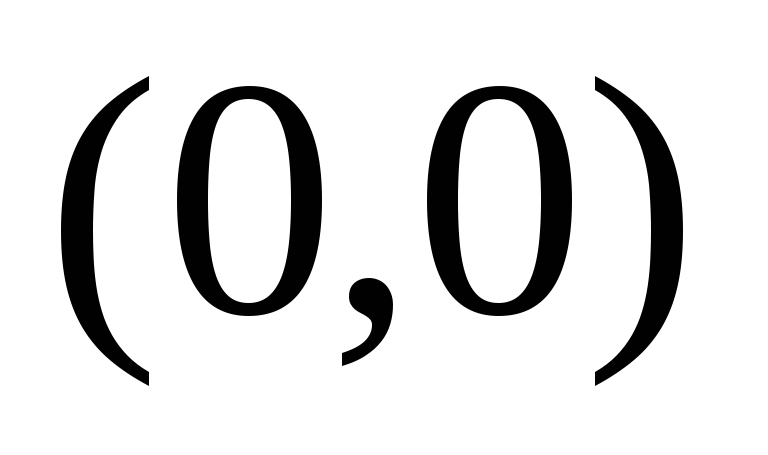 и обратным элементом
и обратным элементом
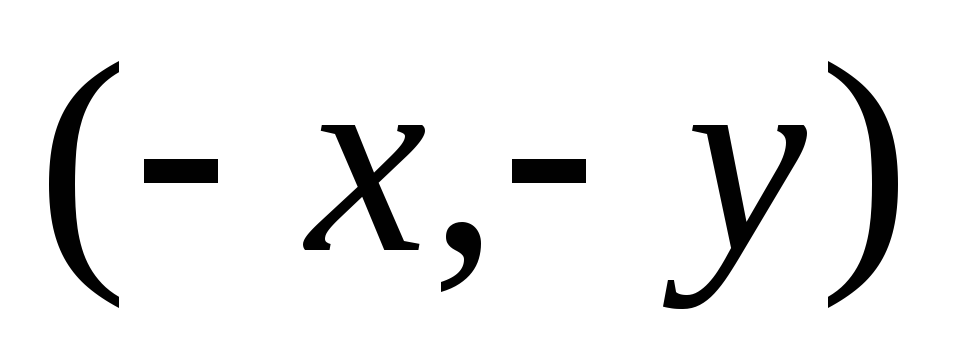 .
. -
Умножение:
 .
Относительно этой бинарной операции
множество
.
Относительно этой бинарной операции
множество
 также является абелевой группой с
единичным элементом
также является абелевой группой с
единичным элементом
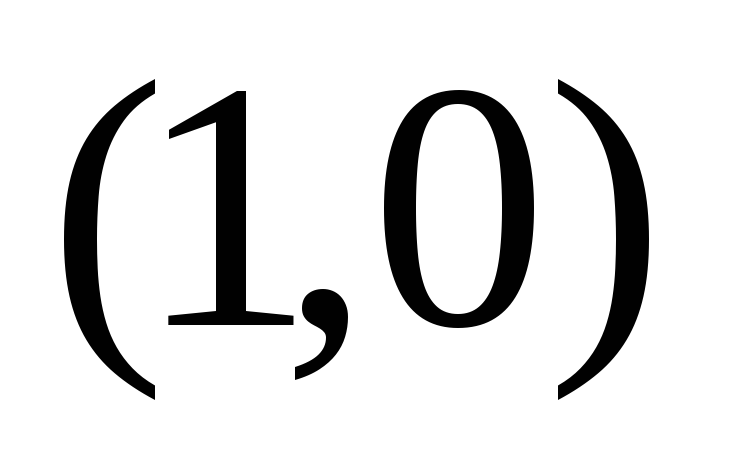 и обратным элементом
и обратным элементом
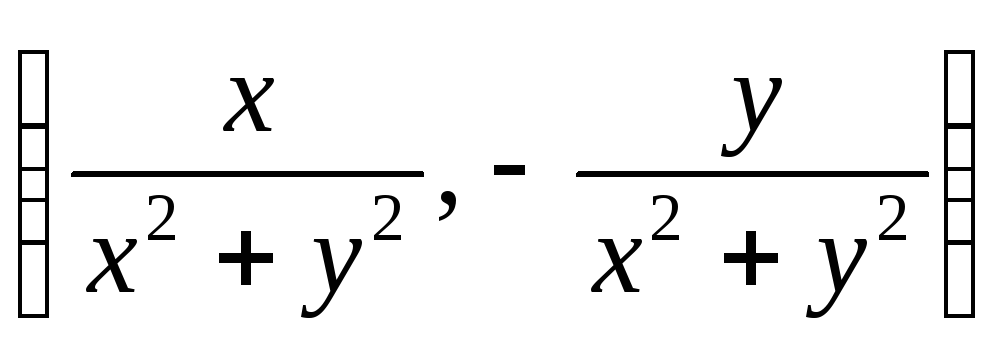 .
.
Можно проверить,
что веденная операция умножения является
дистрибутивной относительно операции
сложения. Следовательно, множество
![]() является полем. Поскольку новые числа
задаются двумя действительными числами,
их иногда называют двумерными числами.
Традиционное название этих чисел –
комплексные
числа. Поле
комплексных чисел обозначается символом
является полем. Поскольку новые числа
задаются двумя действительными числами,
их иногда называют двумерными числами.
Традиционное название этих чисел –
комплексные
числа. Поле
комплексных чисел обозначается символом
![]() .
.
Введем более
удобную форму записи этих чисел,
позволяющую более наглядно проводить
вычисления с этими числами. Образуем
формальную сумму
![]() ,
где символ
,
где символ
![]() удовлетворяет свойству
удовлетворяет свойству
![]() .
Этот символ называют мнимой
единицей.
Такая запись комплексного числа
называется алгебраической
формой комплексного
числа. Если
.
Этот символ называют мнимой
единицей.
Такая запись комплексного числа
называется алгебраической
формой комплексного
числа. Если
![]() ,
то комплексное число отождествляется
с действительным числом, если же
,
то комплексное число отождествляется
с действительным числом, если же
![]() ,
то
,
то
![]() - чисто мнимое число. Действительное
число
- чисто мнимое число. Действительное
число
![]() называют реальной
частью
комплексного числа
называют реальной
частью
комплексного числа
![]() и обозначают
и обозначают
![]() ,
соответственно действительное число
,
соответственно действительное число
![]() называют мнимой
частью комплексного
числа
называют мнимой
частью комплексного
числа
![]() и обозначают
и обозначают
![]() .
.
В новой форме
операции сложения и умножения комплексных
чисел выглядят более естественным
образом:
![]() и
и
![]() .
(Сравните с введенными ранее этими
операциями над комплексными числами).
Чтобы найти обратное число
.
(Сравните с введенными ранее этими
операциями над комплексными числами).
Чтобы найти обратное число
![]() запишем его в виде
запишем его в виде
![]() .
Однако, такая дробь не подходит под нашу
запись комплексного числа. Умножим
числитель и знаменатель этой дроби на
одно и то же комплексное число
.
Однако, такая дробь не подходит под нашу
запись комплексного числа. Умножим
числитель и знаменатель этой дроби на
одно и то же комплексное число
![]() .
Получим
.
Получим
![]() .
Легко проверить, что
.
Легко проверить, что
![]() .
Комплексное число
.
Комплексное число
![]() называется комплексно
сопряженным числом
к числу
называется комплексно
сопряженным числом
к числу
![]() .
При нахождении обратного комплексного
числа
.
При нахождении обратного комплексного
числа
![]() мы, фактически, научились делить
комплексные числа.
мы, фактически, научились делить
комплексные числа.
Пример
1.
![]() .
.
Комплексное
число
![]() или
или
![]() можно изобразить на плоскости
можно изобразить на плоскости
![]() точкой с координатами
точкой с координатами
![]() и
и
![]() .
Плоскость, на которой изображаются
комплексные числа, называется комплексной
плоскостью.
Ось
.
Плоскость, на которой изображаются
комплексные числа, называется комплексной
плоскостью.
Ось
![]() называется действительной
осью (на
ней изображаются действительные числа
называется действительной
осью (на
ней изображаются действительные числа
![]() ),
а ось
),
а ось
![]() - мнимой
осью (на
ней изображаются чисто мнимые числа
- мнимой
осью (на
ней изображаются чисто мнимые числа
![]() ).
Комплексное число можно также изобразить
с помощью радиус-вектора
).
Комплексное число можно также изобразить
с помощью радиус-вектора
![]() точки с координатами
точки с координатами
![]() .
Длина вектора
.
Длина вектора
![]() ,
изображающего комплексное число
,
изображающего комплексное число
![]() ,
называется модулем
этого
комплексного числа и обозначается
,
называется модулем
этого
комплексного числа и обозначается
![]() или
или
![]() .
Очевидно, что
.
Очевидно, что
![]() .
Величина угла между вектором
.
Величина угла между вектором
![]() и осью
и осью
![]() называется аргументом
комплексного
числа и обозначается
называется аргументом
комплексного
числа и обозначается
![]() или
или
![]() .
Аргумент комплексного числа
.
Аргумент комплексного числа
![]() не определен. Аргумент же комплексного
числа
не определен. Аргумент же комплексного
числа
![]() - величина многозначная и определяется
с точностью до слагаемого
- величина многозначная и определяется
с точностью до слагаемого
![]() .
Можно записать
.
Можно записать
![]() ,
где
,
где
![]() - главное
значение аргумента
заключенное (например) в полуинтервале
- главное
значение аргумента
заключенное (например) в полуинтервале
![]() ,
т.е.
,
т.е.
![]() .
Тригонометрическая и показательная
формы комплексного числа.
.
Тригонометрическая и показательная
формы комплексного числа.
Рассмотрим другие
формы записи комплексного числа. Так
как
![]() и
и
![]() ,
то можно записать
,
то можно записать
![]() .
Такая форма записи комплексного числа
называется тригонометрической.
Поскольку
.
Такая форма записи комплексного числа
называется тригонометрической.
Поскольку
![]() и
и
![]() ,
то при переходе от алгебраической формы
комплексного числа к тригонометрической
форме достаточно определить лишь главное
значение аргумента комплексного числа,
т.е. считать
,
то при переходе от алгебраической формы
комплексного числа к тригонометрической
форме достаточно определить лишь главное
значение аргумента комплексного числа,
т.е. считать
![]() .
Если принять, что
.
Если принять, что
![]() лежит в пределах
лежит в пределах
![]() ,
формула
,
формула
![]() приводит к результату
приводит к результату

Для чисел, лежащих на осях, следует помнить, что:
-
для положительной ветви оси

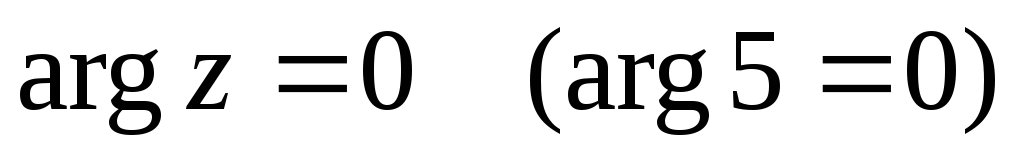 ;
; -
для отрицательной ветви оси
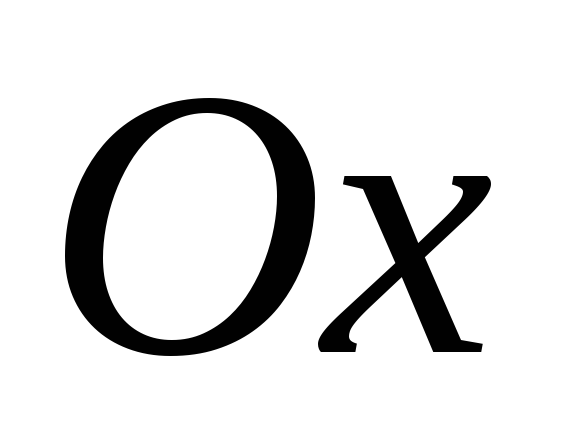
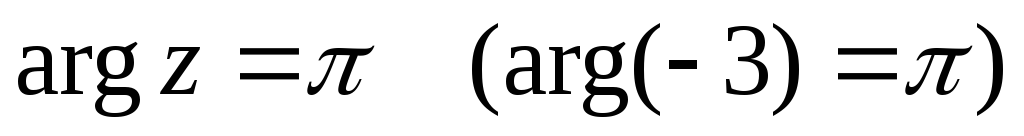 ;
; -
для положительной ветви оси

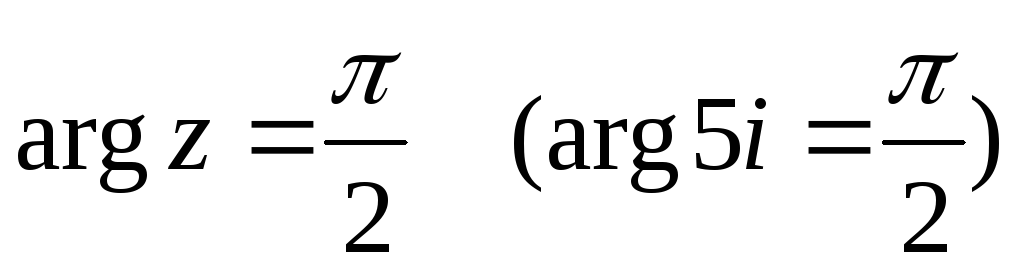 ;
; -
для отрицательной ветви оси
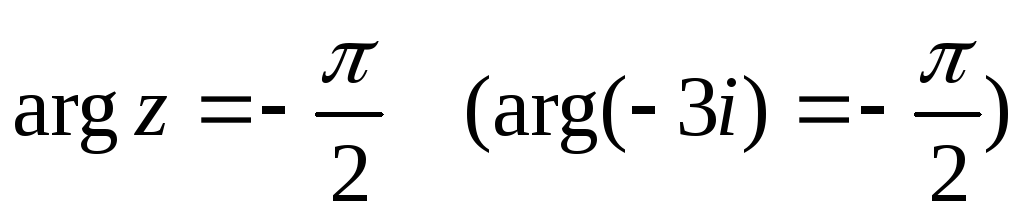 .
.
Если комплексные числа записаны в тригонометрической форме
![]() и
и
![]() ,
то формулы умножения и деления комплексных
чисел имеют вид
,
то формулы умножения и деления комплексных
чисел имеют вид
![]() ,
,
![]() .
.
Очень часто при
вычислениях удобно использовать
показательную
форму
комплексного числа
![]() ,
где
,
где
![]() - основание натуральных логарифмов.
Число
- основание натуральных логарифмов.
Число
![]() - комплексное число, имеющее в алгебраической
форме вид
- комплексное число, имеющее в алгебраической
форме вид
![]() (формула Эйлера). Заметим, что
(формула Эйлера). Заметим, что
![]() .
Законы умножения и деления комплексных
чисел в показательной форме имеют самый
простой вид
.
Законы умножения и деления комплексных
чисел в показательной форме имеют самый
простой вид
![]() и
и
![]() .
.
Пусть
![]() ,
тогда
,
тогда
![]() или
или
![]()
Последняя формула
называется формулой Муавра и используется
при возведении комплексных чисел в
большие степени. С помощью этой формулы
легко получить формулу извлечения корня
какой-либо степени из комплексного
числа. Если
![]() ,
то
,
то
![]() или
или
![]() .
.
Для числа
![]() следует взять значения
следует взять значения
![]() .
.
Пример
2.
Вычислим
![]() .
Запишем подкоренное выражение в
тригонометрической форме
.
Запишем подкоренное выражение в
тригонометрической форме
![]() ,
так как
,
так как
![]() и
и
![]() .
Следовательно,
.
Следовательно,
![]() ,
где
,
где
![]() .
Находим три корня:
.
Находим три корня:
![]() ;
;
![]() ;
;
![]() .
.
Замечание.
Попытка ввести «трехмерные числа
![]() »
по аналогии с двумерными числами
»
по аналогии с двумерными числами
![]() потерпела неудачу. Однако, У. Гамильтону
удалось определить «четырехмерные
числа»
потерпела неудачу. Однако, У. Гамильтону
удалось определить «четырехмерные
числа»
![]() - кватернионы, в которых имеются три
мнимых единицы
- кватернионы, в которых имеются три
мнимых единицы
![]() .
При введении этих гиперкомплексных
чисел пришлось отказаться от свойства
коммутативности
.
При введении этих гиперкомплексных
чисел пришлось отказаться от свойства
коммутативности
![]() .
Доказано, что в пространствах большей
размерности построение таких систем
- «чисел» невозможно.
.
Доказано, что в пространствах большей
размерности построение таких систем
- «чисел» невозможно.
ЗАДАЧИ
1. Задачи удовлетворительного уровня сложности.
Построить на комплексной плоскости точки.
4.1.
![]() .
4.2.
.
4.2.
![]() .
4.3.
.
4.3.
![]() .
4.4.
.
4.4.
![]() .
4.5. 1. 4.6. -1. 4.7.
.
4.5. 1. 4.6. -1. 4.7.
![]() .
4.8.
.
4.8.
![]() .
.
Для данных
комплексных чисел найти
![]() .
.
4.9. 5. 4.10.
![]() .
4.11.
.
4.11.
![]() .
4.12
.
4.12
![]() .
4.13
.
4.13
![]() .
4.14
.
4.14
![]() .
4.15.
.
4.15.
![]() .
.
4.16.
![]() .
4.17.
.
4.17.![]() .
.
Построить на
комплексной плоскости
![]() векторы, соответствующие комплексным
числам
векторы, соответствующие комплексным
числам
![]() .
Найти
.
Найти
![]() и
и
![]() .
.
4.18.
![]() .
4.19.
.
4.19.
![]() .
4.20.
.
4.20.
![]() .
4.21.
.
4.21.
![]() .
4.22.
.
4.22.
![]() .
.
4.23.
![]() .
.
Записать в алгебраической форме числа.
4.24.
![]() .
4.25.
.
4.25.
![]() .
4.26
.
4.26
![]() .
.
Записать в тригонометрической форме комплексные числа.
4.27.
![]() .
4.28.
.
4.28.
![]() .
4.29.
.
4.29.
![]() .
4.30.
.
4.30.
![]() .
.
4.31.
![]() .
4.32.
.
4.32.
![]() .
4.33.
.
4.33.
![]() .
.
4.34.
![]() .
4.35
.
4.35
![]() .
4.36.
.
4.36.
![]() .
.
4.37.
![]() ,
где
,
где
![]() .
.
Записать в показательной форме комплексные числа.
4.38.
![]() .
4.39.
.
4.39.
![]() .
4.40.
.
4.40.
![]() .
4.41.
.
4.41.
![]() .
4.42.
.
4.42.![]() .
.
4.43.
![]() .
4.44.
.
4.44.
![]() .
.
Изобразить на
комплексной плоскости
![]() множества точек, удовлетворяющих
условиям.
множества точек, удовлетворяющих
условиям.
4.45.
![]() .
4.46.
.
4.46.
![]() .
4.47.
.
4.47.
![]() .
4.48.
.
4.48.
![]() .
.
4.49.
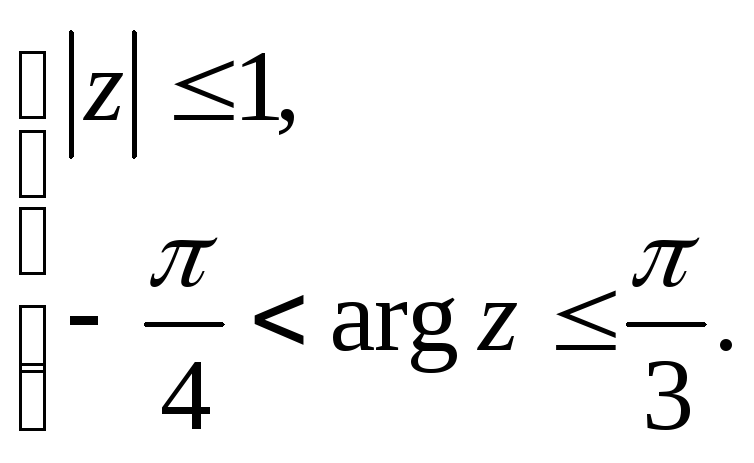 4.50.
4.50.
![]() .
.
4.51.
![]() .
.
4.52. Найти
наибольшее и наименьшее значения
![]() ,
если
,
если
![]() .
.
4.53. Могут ли быть комплексно сопряженными: два действительных числа? два чисто мнимых числа? действительное и мнимое число?
4.54. Пусть
![]() .
Чему равен
.
Чему равен
![]() ?
?
4.55. Как выглядят условия равенства двух комплексных чисел, заданных в тригонометрической форме?
4.56. Какое из
чисел больше:
![]() или
или
![]() ?
?
4.57. Найти
![]() ,
если
,
если
![]() .
.
Вычислить комплексные числа.
4.58.
![]() .
4.59.
.
4.59.
![]() .
4.60.
.
4.60.
![]() .
.
4.61.
![]() .
4.62.
.
4.62.
![]() .
4.63.
.
4.63.
![]() .
4.64.
.
4.64.
![]() .
.
4.65.
![]() .
4.66.
.
4.66.
![]() .
4.67.
.
4.67.
![]() .
4.68.
.
4.68.
![]() .
.
4.69.
![]() .
4.70.
.
4.70.
![]() .
4.71.
.
4.71.
![]() .
.
4.72.
![]() .
4.73.
.
4.73.
![]() .
4.74.
.
4.74.
![]() .
4.75.
.
4.75.
![]() ;
;
4.76.
![]() .
4.77.
.
4.77.
![]() .
.
Найти все значения корней.
4.78.
![]() .
4.79.
.
4.79.
![]() .
4.80.
.
4.80.
![]() .
4.81.
.
4.81.
![]() .
4.82.
.
4.82.
![]() .
4.83.
.
4.83.
![]() .
.
4.84.
![]() .
4.85.
.
4.85.
![]() .
4.86
.
4.86
![]() .
4.87.
.
4.87.
![]() .
4.88.
.
4.88.
![]() .
.
4.89.
Сколько и каких значений имеет произведение
![]() ?
?
Решить уравнения
![]() .
.
4.90.
![]() .
4.91.
.
4.91.
![]() .
.
Данные числа
![]() и
и
![]() записать в показательной форме и
выполнить над ними указанные действия.
записать в показательной форме и
выполнить над ними указанные действия.
4.92.
![]() ,
где
,
где
![]() .
.
4.93.
![]() ,где
,где
![]() .
.
Доказать равенства.
4.94.
![]() .
4.95.
.
4.95.
![]() .
.
Используя формулу Эйлера, получить соотношения.
4.96.
![]() .
4.97.
.
4.97.
![]() .
.
4.98.
![]() .
4.99.
.
4.99.
![]() .
.
Используя формулу Эйлера, выразить через косинусы и синусы кратных дуг функции.
4.100.
![]() .
4.101.
.
4.101.
![]() .
4.102.
.
4.102.
![]() .
.
Используя формулу Муавра, доказать справедливость тождеств.
4.103.
![]() .
4.104.
.
4.104.
![]() .
.
Найти действительные решения уравнений.
4.105.
![]() .
4.106.
.
4.106.
![]() .
.
Вычислить модули комплексных чисел.
4.107.
![]() .
4.108.
.
4.108.
![]() .
.
4.109. Может ли сумма квадратов двух комплексных чисел быть отрицательной?
4.110. Как изменится
модуль и аргумент комплексного числа
![]() в
в
результате умножения этого числа на комплексные числа: а) 2;
б)
![]() ;
в)
;
в)
![]() ?
?
2. Задачи повышенного уровня сложности.
Используя формулу Муавра, записать комплексные числа в алгебраической форме.
4.111.
![]() .
4.112.
.
4.112.
![]() .
4.113
.
4.113
![]() .
.
4.114.![]() .
.
Найти все значения корней.
4.115.
![]() .
4.116.
.
4.116.
![]() .
4.117.
.
4.117.
![]() .
.
4.118. Выразить
через синус и косинус кратных дуг: а)
![]() ,
б)
,
б)
![]() .
.
4.119. Составить таблицу умножения группы, элементами которой являются корни пятой степени из единицы.
4.120. Показать,
что комплексные числа, обладающие
свойством
![]() ,
образуют группу с групповой операцией
– умножение.
,
образуют группу с групповой операцией
– умножение.
4.121. Найти действительные и комплексные решения системы уравнений:
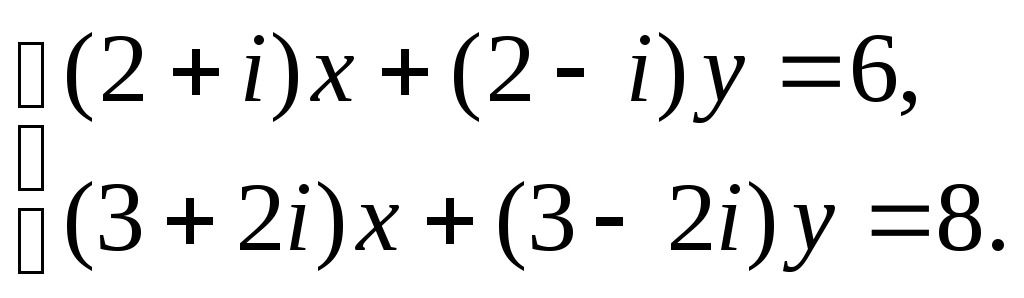
Решить уравнения.
4.122.
![]() .
4.123.
.
4.123.
![]() .
4.124.
.
4.124.
![]() .
.
4.125.
![]() .
.
4.126. Дано
комплексное число
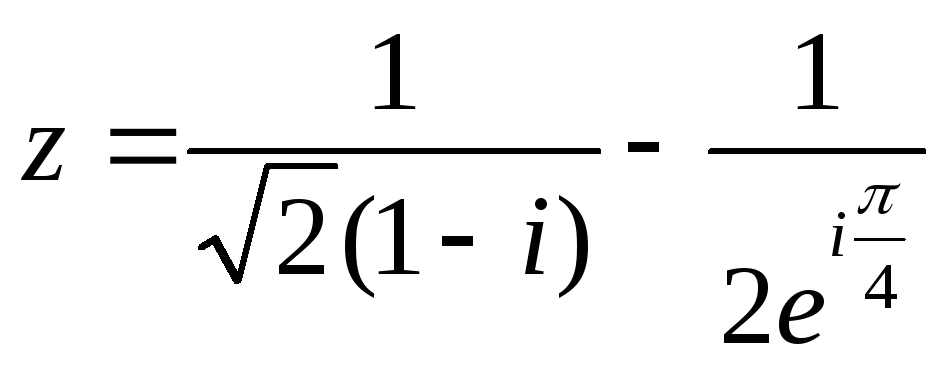 .
Найти:
.
Найти:
![]() и
и
![]() .
.
4.127. Найти комплексные числа, каждое из которых сопряжено со своим квадратом.
4.128. Найти
![]() .
.
4.129. При каком
условии квадрат комплексного числа
![]() является чисто мнимым числом?
является чисто мнимым числом?
4.130. Указать на
комплексной плоскости точки
![]() ,
для которых:
,
для которых:
а)
![]() ;
б)
;
б)
![]() .
.
