I. Определение группы.

При определении бинарных операций на множествах произвольной природы удобно сохранить термины умножение и произведение и записывать бинарную операцию в виде или же (в некоторых случаях)сложение и сумма и использовать аддитивную запись: .

Определение. Множество называетсягруппой, если выполнены следующие условия:

1. на множестве введена бинарная операция;

2. введенная бинарная операция является ассоциативной:

;

3. множество содержитединичный элемент 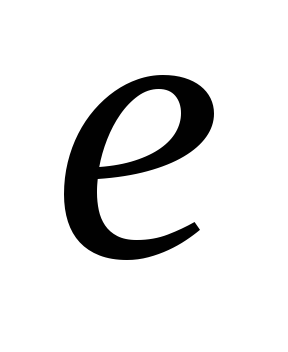, обладающий свойством 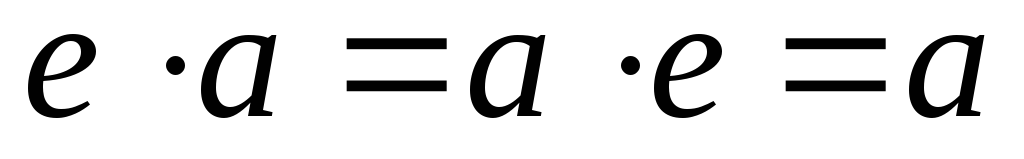для всех ;

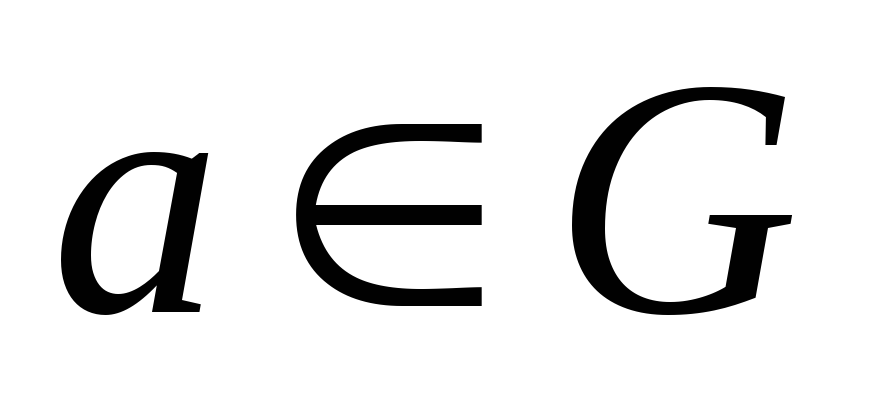4. для любого элемента 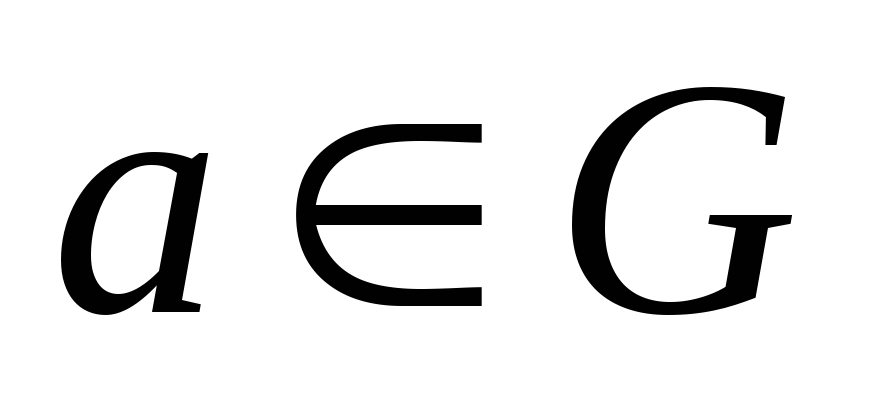существуетобратный элемент 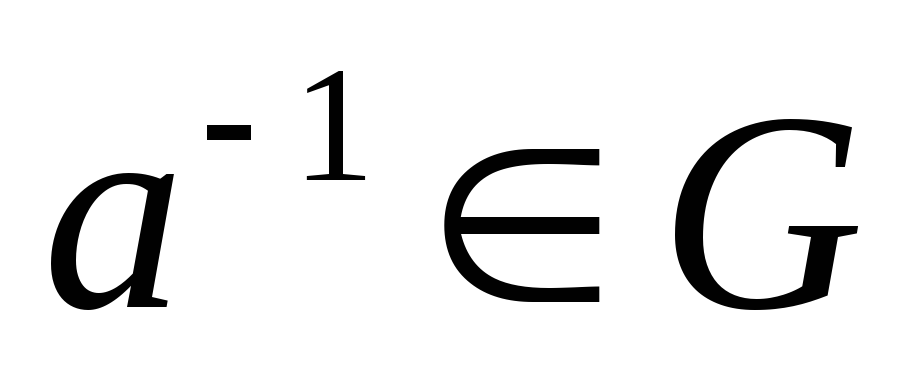такой, что.

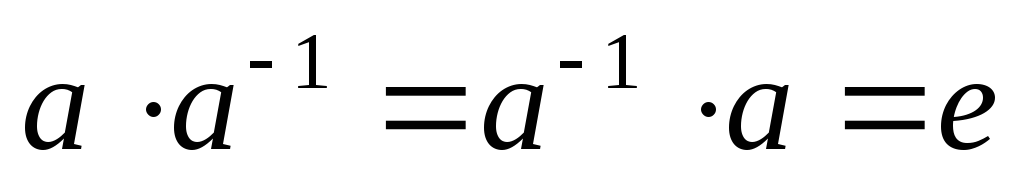Пример 3. Пусть . В качестве бинарной операции на множестве целых чисел рассмотрим обычное сложение. Эта операция удовлетворяет всем трем необходимым условиям группы:

1. ассоциативность - ;

2. единичным элементом 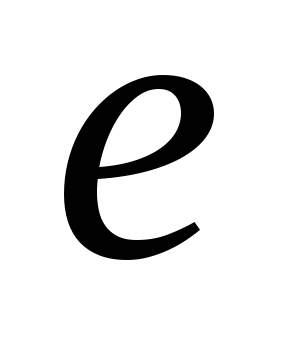является;

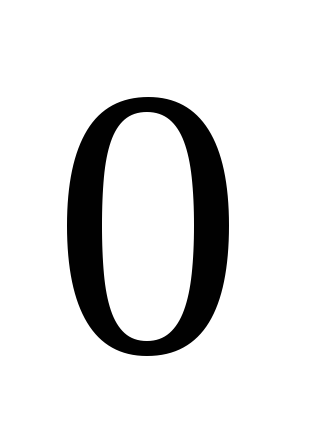3. обратным элементом к 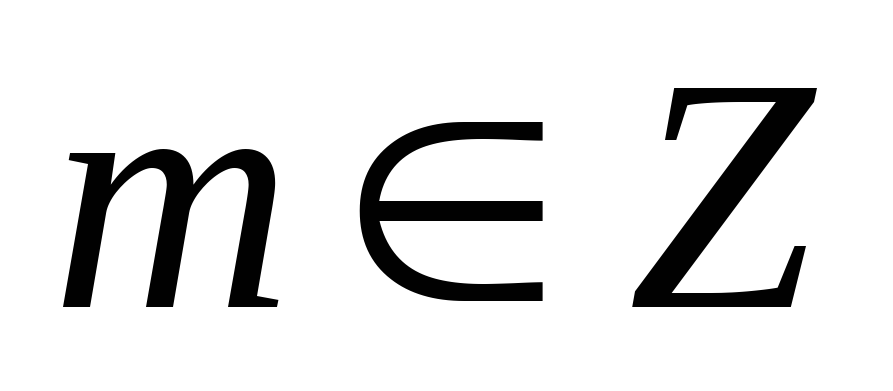будет элемент().

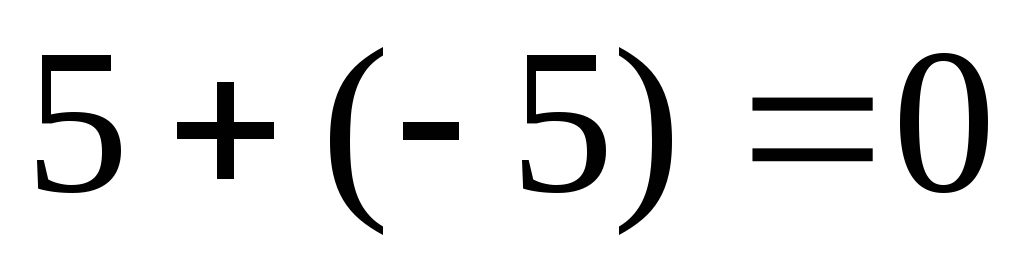Следовательно, множество целых чисел является группой с бинарной операцией – сложение.

Определение. Два элемента игруппыкоммутируют друг с другом, если .

Определение. Если все элементы группы коммутируют друг с другом, то такая группа называется коммутативной или абелевой. Если какие-либо элементы группы не коммутируют друг с другом, то такая группа называется неабелевой.

Определение. Число элементов в группе называетсяпорядком этой группы.

Определение. Если число элементов в группе конечно, то такая группа называется конечной группой. Если же группа содержит счетное число элементов, то ее называют бесконечной дискретной группой (например, ).

Наряду с дискретными группами в современной физике часто рассматриваются непрерывные группы (топологические группы или группы Ли).

Определение. Если все элементы группы (включая единичный элемент) представимы в виде степени одного элемента, то группа называется циклической и обозначается , где- порядок группы. Группаможет быть реализована вращениями вокруг своего центра многоугольника в его плоскости, совмещающими многоугольник с самим с собой. Обозначим элемент группы(вращение на угол) через. Закон композиции в группе введем правилом. Очевидно, что- единичный элемент группы, а элементявляется обратным элементом к элементу. Любое рассматриваемое вращение многоугольника представимо в виде некоторой степени вращения на угол, где- число углов рассматриваемого многоугольника, т.е..

Определение. Симметрической группой степени называется группа перестановок множества из элементов. Под перестановкой же понимается взаимно однозначное отображение множества на себя, при этом элементы множества меняются местами (или именами). Поскольку для перестановки не важна природа элементов множества, а только их порядок (или их номера) перестановку можно задать таблицей. Например, перестановка, заданная таблицей

,

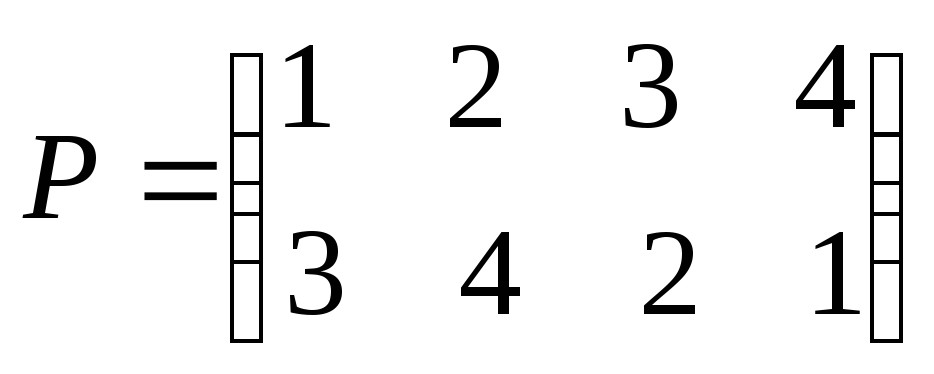говорит нам, что первый элемент становится третьим, второй – четвертым, третий – вторым, а четвертый – первым. Закон композиции в симметрической группе задается следующим образом. Пусть заданы две перестановк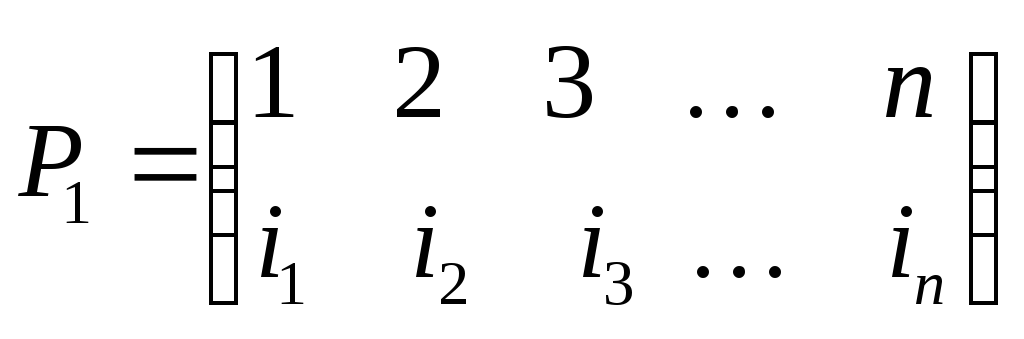и и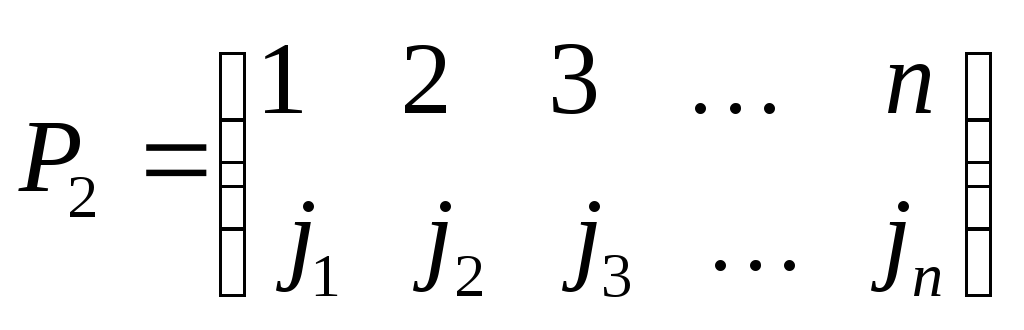. Переставим столбцы таблицы, соответствующей второй перестановке, так, чтобы ее верхняя строчка совпала бы с нижней строчкой таблицы первой перестановки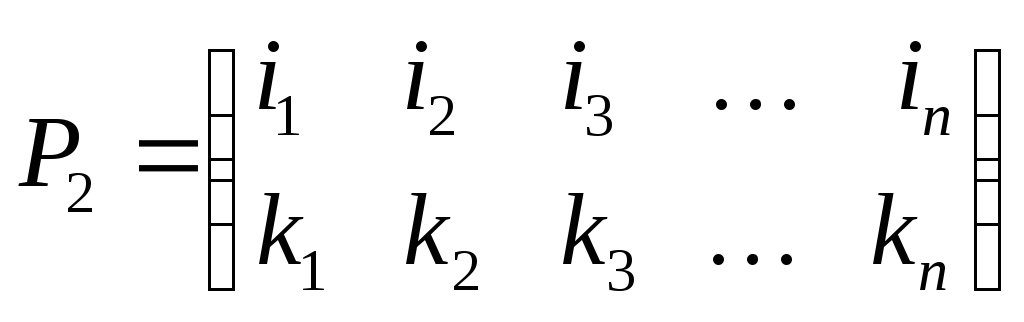. Тогда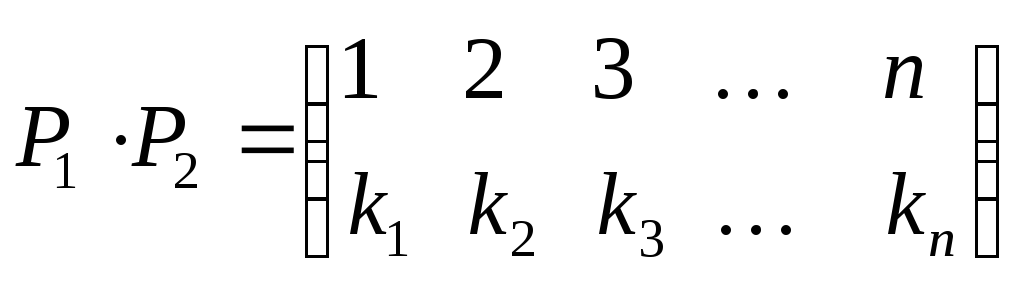. Заметим, что перестановка столбцов таблицы, не меняет саму перестановку.

Пример 4. Пусть 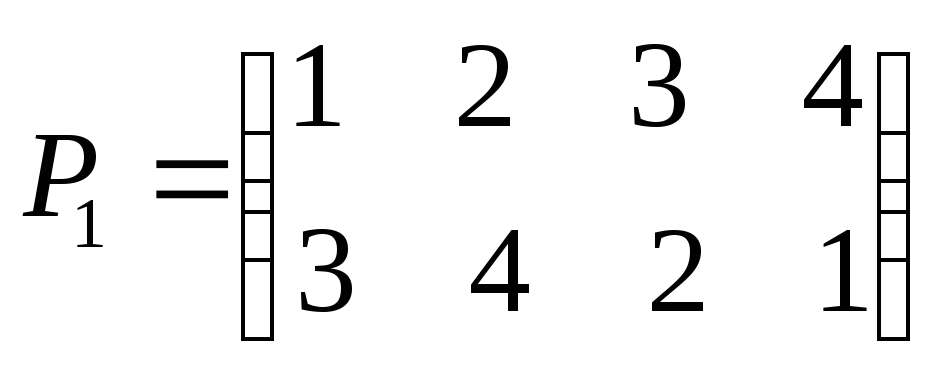и. Тогда

.

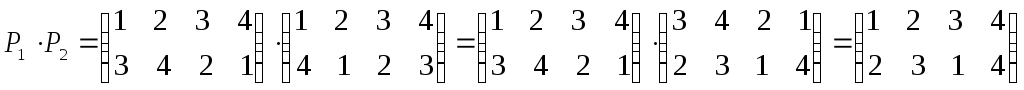II. Таблица умножения группы.

Для задания той или иной группы достаточно построить ее таблицу умножения. Она похожа на привычную арифметическую таблицу умножения. Элементы группы располагаются в верхней строке и в том же порядке в левом столбце таблицы, а внутри нее размещаются произведения элементов

Пример 5. Рассмотрим симметрическую группу 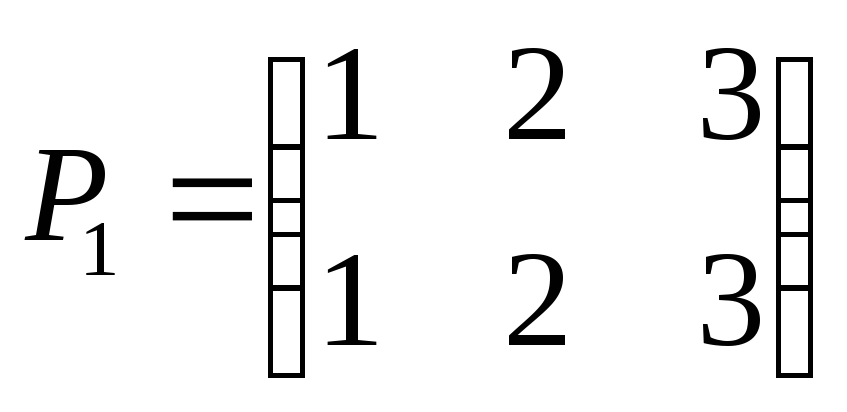, элементами которой являются перестановки:- тождественная перестановка (единичный элемент группы),,,,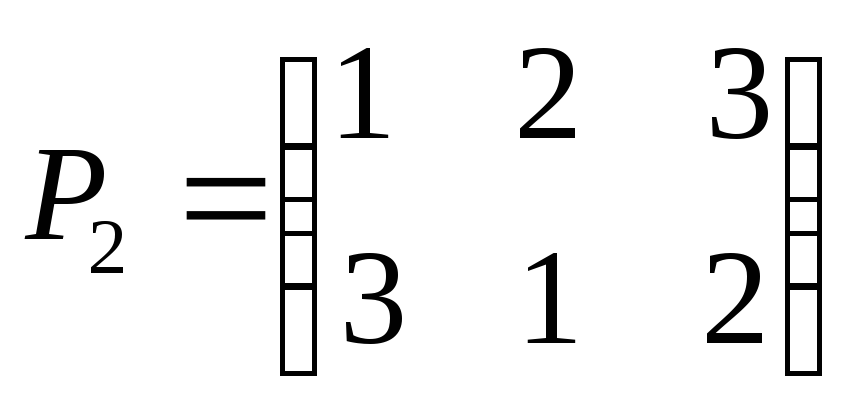

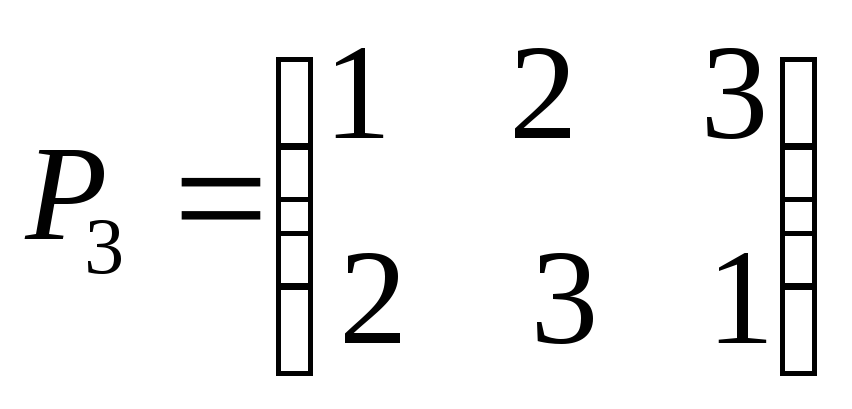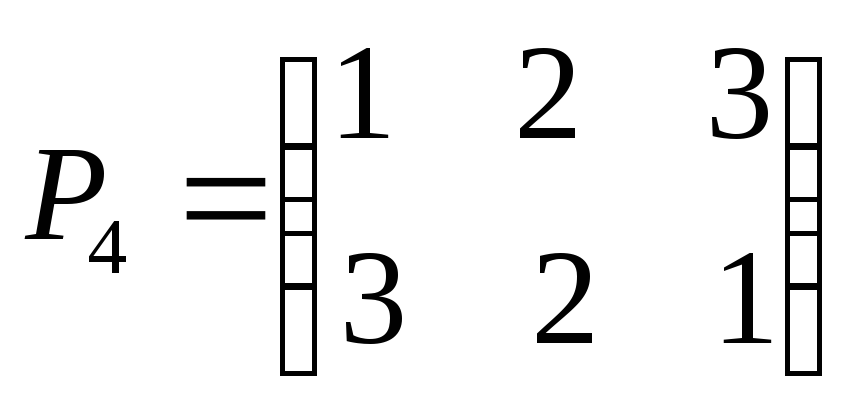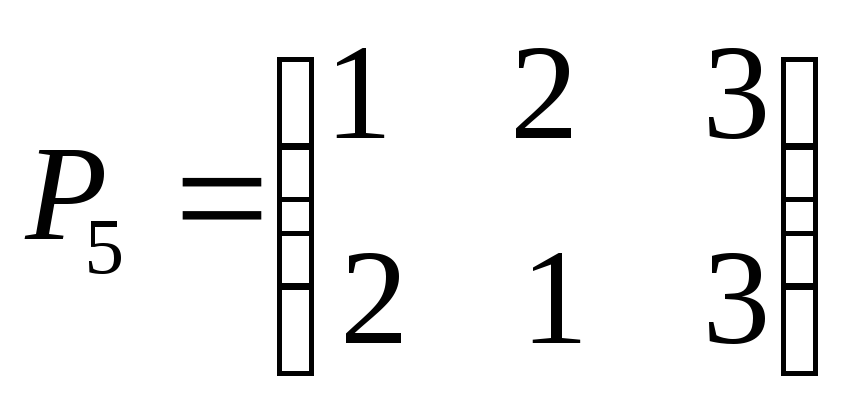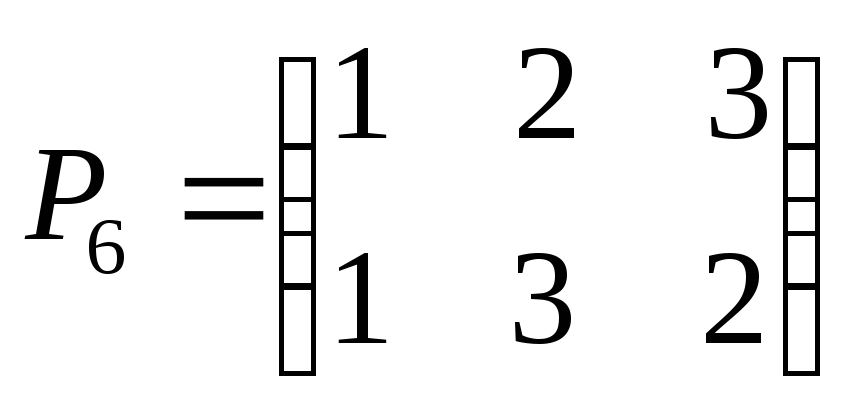, . Таблица умножения этой группы имеет вид

.

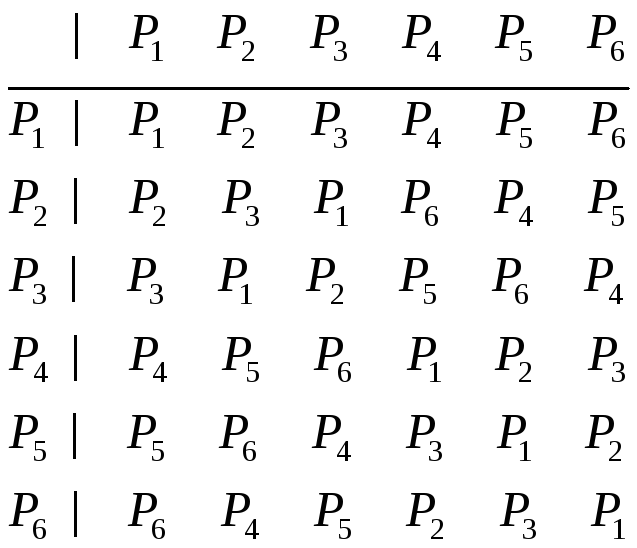Отметим основные свойства таблицы умножения любой группы (для группыих легко увидеть в приведенном выше примере):

1. Если группа имеет 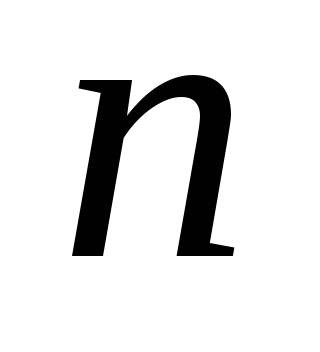элементов, то ее таблица умножения имеет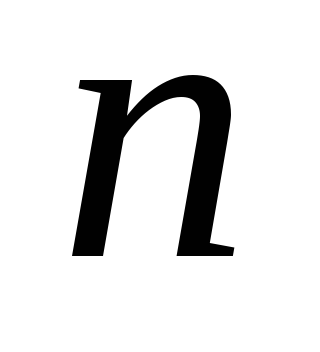строк и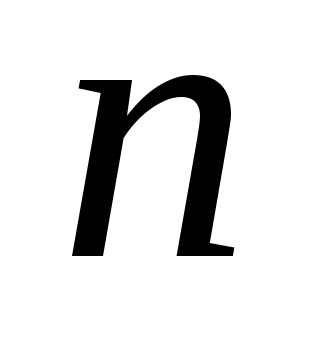столбцов, т.е. является квадратной с общим числом символов.

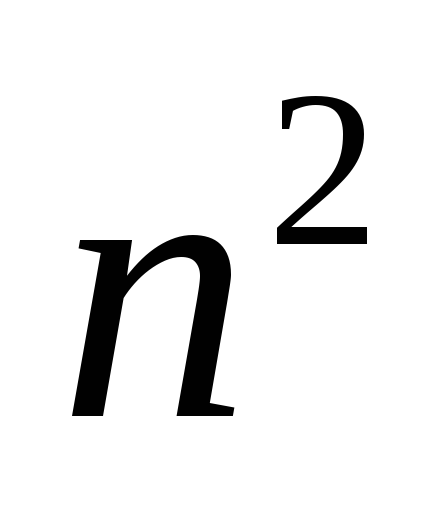2. Таблица содержит только элементы группы, причем в каждой строке и в каждом столбце эти элементы различные. Следовательно, каждая строка и каждый столбец содержит все элементы группы.

3. Имеются только одна строка и один столбец, в которых элементы группы стоят в том же порядке, в котором они стоят над таблицей или левее таблицы (эти строка и столбец задаются единичным элементом группы и отражают свойства единичного элемента).

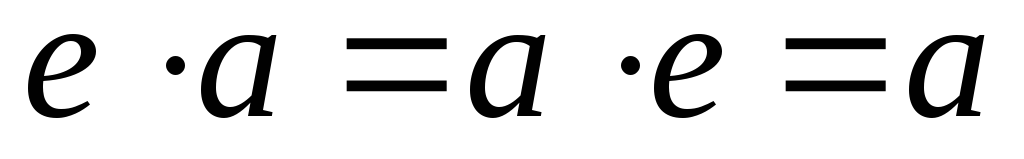4. Таблица умножения абелевой группы симметрична относительно главной диагонали (симметрическая группа не является абелевой: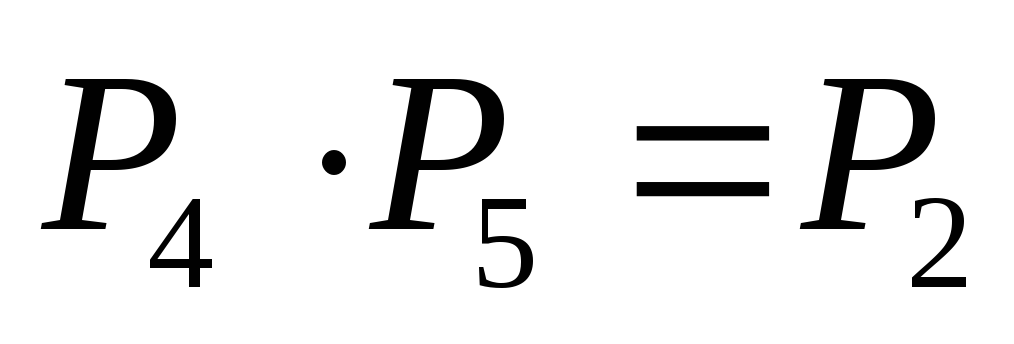, в то время как).

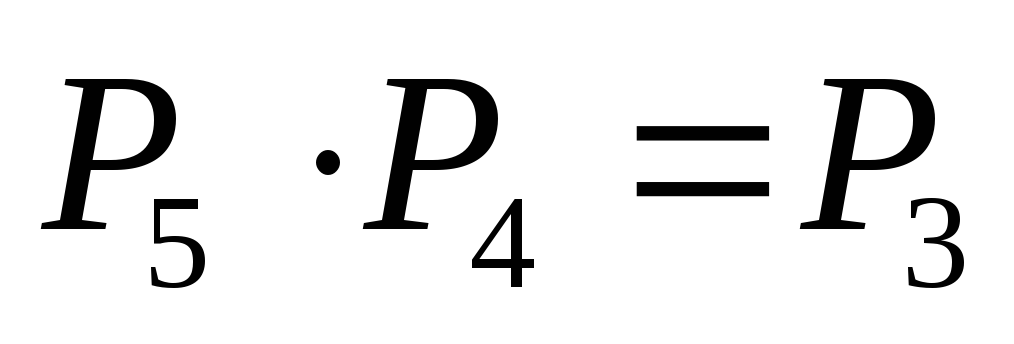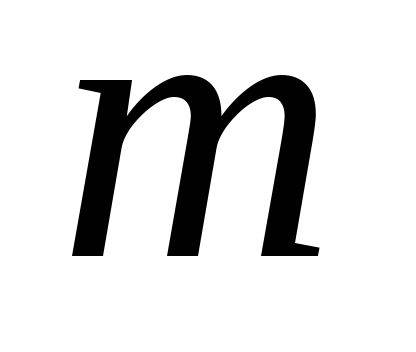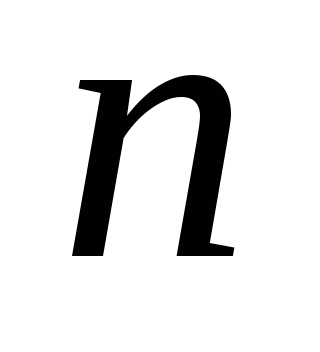5. Возьмем какую-либо строку таблицы умножения группы (скажем под номером ) и найдем в ней единичный элемент. Пусть он принадлежит столбцу под номером. Тогда на пересечении строки с номером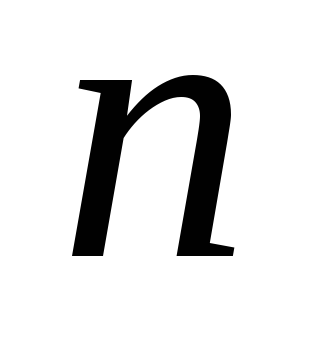и столбца с номером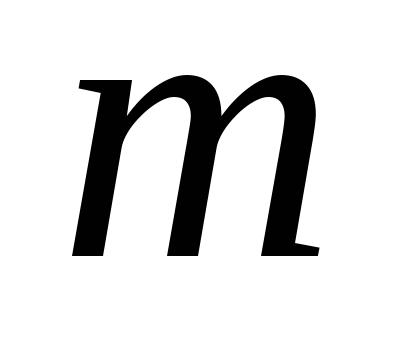стоит также единичный элемент группы, т.е. единичные элементы группы стоят в таблице умножения либо на главной диагонали, либо симметрично относительно нее. Это свойство таблицы отражает свойство обратного элементаи позволяет легко находить обратные элементы. Например, элементстоит в третьей строке, а единичный элемент в этой строке находится во втором столбце, следовательно, элементы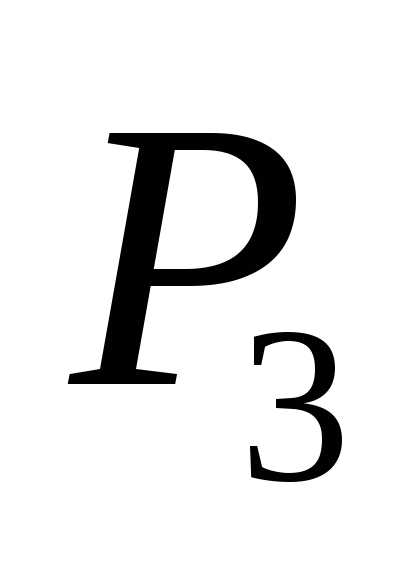и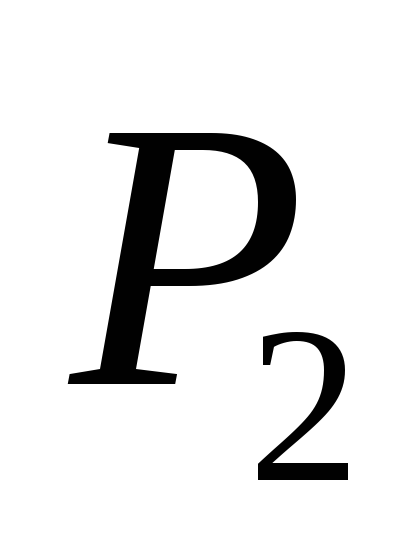взаимно обратны.

Определение. Пусть и.Порядком элемента называется наименьшее положительное число, удовлетворяющее условию. Очевидно, что для циклических групп порядок элемента равен порядку группы.

Определение. Если - множество элементов, принадлежащих группе, таких, что все элементы группымогут быть выражены в виде произведений элементов из(и их обратных), то множествоназываетсясистемой образующих группы (сами же элементы множестваназываютсяобразующими группы ).

Поскольку каждый элемент циклической группы представляется степенью одного элемента этой группы, то эта группа имеет одну образующую. Симметрическая группа имеет две образующие, например,

.

Определение. Множество называетсяподгруппой группы , если

1. каждый элемент множества является элементом группы;

2. есть группа относительно закона композиции, определенного в группе .

Проверка факта, что подмножество , является подгруппой группы, сводится к проверке трех условий:

1. ;

2. ;

3. .

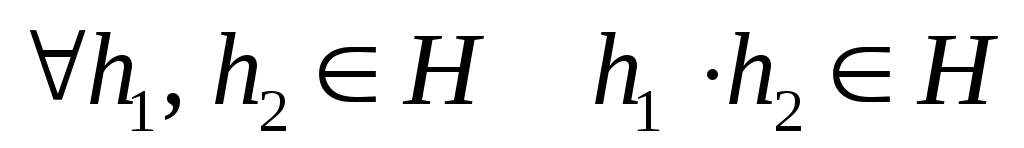Любая группа имеет две тривиальные подгруппы – единичный элемент и сама группа. Эти две подгруппы называютсянесобственными подгруппами группы , остальные ее подгруппы (если они существуют) называютсясобственными подгруппами.

Пример 6. Множества иявляются собственными подгруппами симметрической группы.

III. Отображения групп. Теорема Кэли.

Определение. Пусть мы имеем две группы и, а также отображениегруппына группу. Если это отображение сохраняет групповую операцию –образ произведения двух элементов равен произведению их образов, т. е. , то отображениеназываетсягомоморфным отображением или гомоморфизмом.

Пример 7. Рассмотрим две циклические группы и. Гомоморфизмом будет отображение, заданное правилом.

Определение. Взаимно однозначное гомоморфное отображение одной группы на другую называется изоморфным отображением или изоморфизмом. Сами группы при этом называют изоморфными.

Изоморфные группы имеют одинаковое число элементов и одинаковую групповую структуру.

Пример 8. Группа вращений пятиугольника изоморфна группе, в которой закон композиции – сложение по модулю пять. Таблица умножения такой группы имеет вид

.

Изоморфизмом является отображение , заданное правилом

.

Симметрические группы играют особую роль в теории групп, о чем говорит теорема Кэли.

Теорема Кэли. Всякая группа порядкаизоморфна некоторой подгруппе симметрической группе.

Следовательно, задачу изучения структуры всех конечных групп можно перевести в плоскость изучения подгрупп симметрических групп.

IV. Смежные классы. Теорема Лагранжа.

Рассмотрим группу порядка, которая имеет собственную подгруппупорядка. Пустьсостоит из элементов. Так как, то в группенайдется элемент, не принадлежащий подгруппе. Образуем множество произведений элементасо всеми элементами подгруппы:. Все элементы множества

различны и не принадлежат подгруппе . Если в группенайдется элемент, не принадлежащий множествами, то образуем множество. Все элементы множества

различны и не принадлежат множествам и. Повторяем эту процедуру до тех пор, пока на исчерпаем все элементы группы. Пусть последним мы образовали множество. Множества вида(включая саму подгруппу) называютлевыми смежными классами подгруппы в группе. При этом справедливо равенство

.

Более точно левые смежные классы образуют разбиение группы . Следовательно,. Это равенство формулируется в виде теоремы.

Теорема Лагранжа. Порядок подгруппы конечной группы есть делитель порядка группы.

Пример 9. Рассмотрим симметрическую группус ее отмеченной выше подгруппой. Образуем левый смежный класс. Классыиполностью исчерпывают группу. Следовательно,. Возможен другой вариант.

Аналогичным образом можно построить правые смежные классы . В общем случае.

Если порядок группы – простое число, то она не имеет собственных подгрупп. Все группы такого порядка – циклические группы.