3.5. Степени свободы. Статическая определимость.

Систему, неизменяемость которой доказана, называют диском. Каждый диск в плоскости имеет три степени свободы: возможность перемещения вдоль каждой из пересекающихся осей и поворота (рис.1.15).

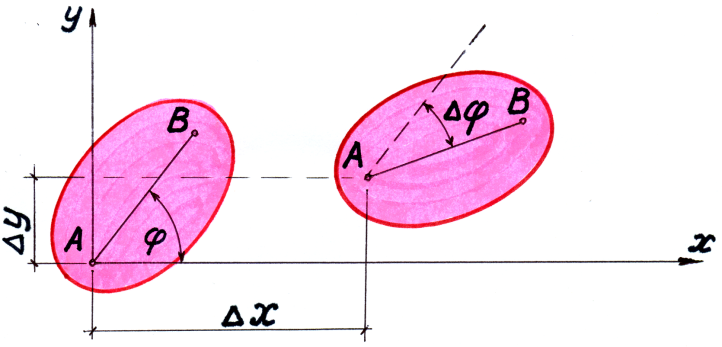
Рис.3.15.

Каждая опора диска отнимает у последнего определённое число степеней свободы: шарнирно подвижная- одну, шарнирно неподвижная – две, заделка-три.

Одна связь отнимает одну степень свободы. У шарнирно подвижной опоры одна связь, у шарнирно неподвижной-две, у заделки- три. Для системы из D дисков степень статистической определимости

где Ш - число однократных промежуточных шарниров (кратность узла ), С-число степеней свободы, отнимаемых у системы опорами (внешними связями).

При имеем механизм: изменяемую систему,

при – статически определимую систему,

при - статически неопределимую систему.

Реальные сооружения должны быть неизменяемыми системами, способными воспринимать нагрузку без заметного изменения геометрической формы.

Cтержневая система называется геометрически неизменяемой, если невозможны перемещения её точек без изменения длин стержней. Неизменяемая система способна воспринимать нагрузку до наступления разрушения материала.

В статически определимой системе усилия могут быть найдены с помощью уравнений равновесия.

В статически неопределимых системах приходиться дополнительно использовать условия совместности деформаций.

ТЕОРЕМА:

неизменяемые системы, все связи которых необходимы, являются статически определимыми системами.

Для балки на двух опорах и рамы (рис.3.14)

т.е. они статически определимы.

Для фермы на рис.3.16 цифрами около каждого узла показана кратность шарнира (каждый однократный шарнир в системе из дисков эквивалентен наложению двух связей).

Рис.3.16.

D=17, Ш=24, С=3.

Ферма также статистически определима.

Для рамы на рис.3.17.

т.е. она 9 раз статически неопределима.

В раме на рис.3.18 с жёсткими узлами имеются замкнутые контуры. Приведенный здесь способ определения статической определимости для неё не подходит.

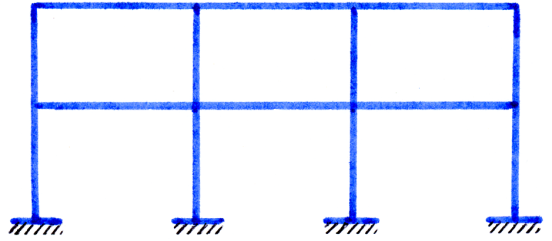
Рис.3.17. Рис.3.18.

4. Виды стержневых систем.

4.1. Балки.

Различают следующие виды балок.

Консольные балки (рис.2.14).

Двух опорные балки (рис.2.12,2.13,2.15), в т.ч. консольно-пролётные (рис.2.15).

Составные (многошарнирные) балки (рис.4.1).

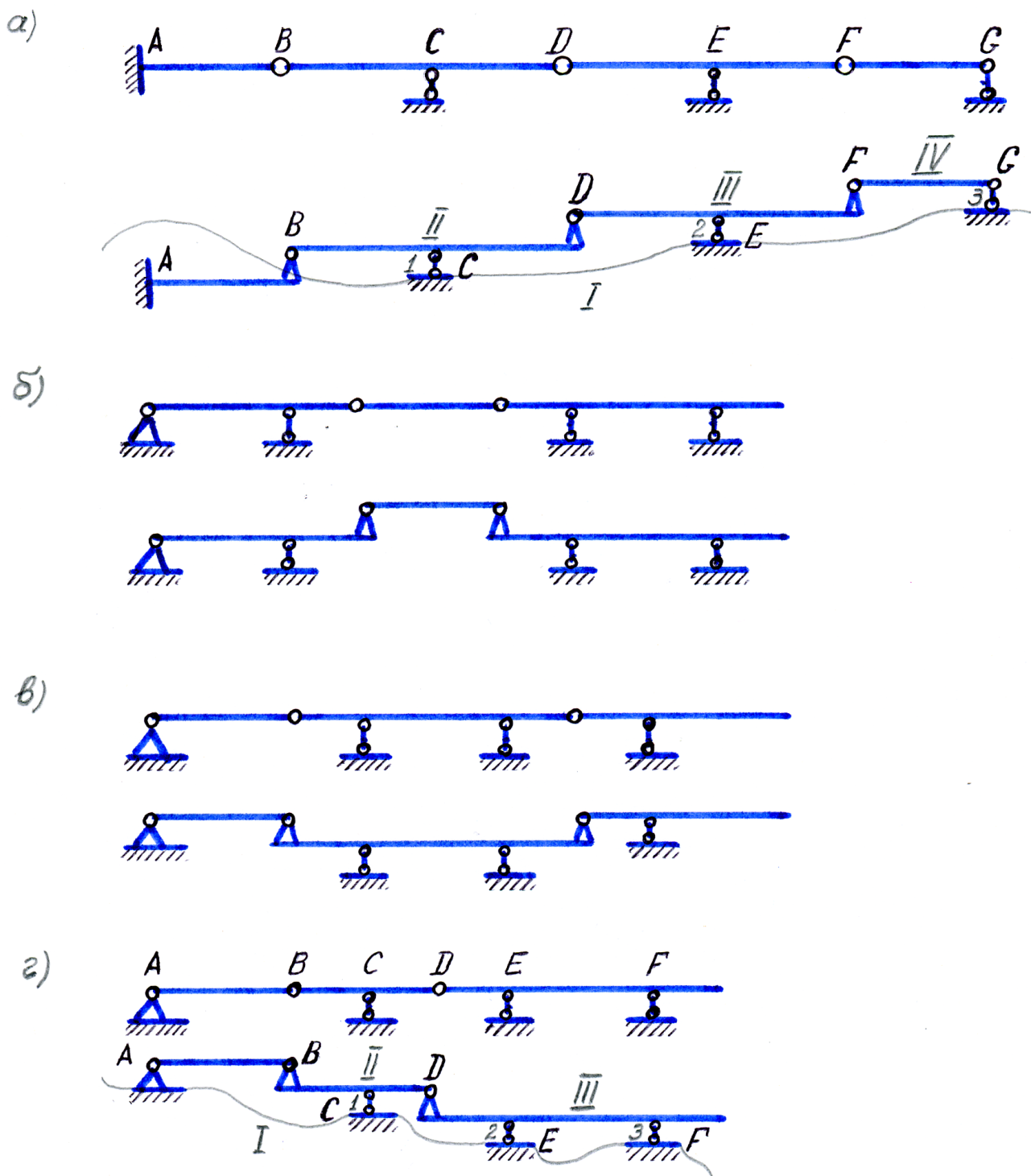
Рис.4.1. Составные балки и их поэтажные схемы.

Многопролётные балки (рис.4.2)

Рис.4.2. Многопролётная нарезная балка.

Исследуем их образование на примере балки (а) (рис.4.1а).

На её поэтажной схеме основание обозначено цифрой I.В него включена и жёстко присоединённая консольная балка АВ. К основанию присоединён диск II шарниром В и стержнем 1 (ось стержня 1 не пересекает шарнир В). Следовательно, диски I и II можно объединить в единый диск, к которому диск III присоединён шарниром D и стержнем 2 и т.д. Т.е. система на рис.4.1а является геометрически неизменяемой. Кроме того, имеет только необходимые стержни ( Поэтому статически определима.

В составной балке на рис.4.1г диск II соединён с диском I двумя стержнями (1 и АВ), оси которых пересекаются в точке С. Диск III соединён с основанием диска I двумя параллельными стержнями:2 и 3, точка пересечения которых находится в бесконечности. Диски II и III соединены шарниром D. Таким образом, имеем случай соединения трёх дисков с помощью шарнира и четырёх стержней. Причём точка пересечения стержней и шарнир не лежат на одной прямой. Система дисков I, II и III представляет собой неизменяемую систему.

Кроме того, эта система является и статически определимой, т.к. для неё

Аналогично можно доказать неизменяемость и статическую определимость балок, изображённых на рис.4.1б и 4.1в.

При определении опорных реакций и усилий в составных балках после составления поэтажной схемы расчёт начинают с верхней балки и заканчивают самой нижней.

Многопролётная балка- это балка, которая покоится на нескольких промежуточных опорах (рис.4.1 и 4.2).