1.3 Сложение нескольких сил, сходящихся в одной точке.

Полигоном нескольких векторов называется ломаная, составленная из этих векторов так, что конец одного из них совпадает с началом второго, конец второго – с началом третьего и т.д.

Суммой нескольких векторов называется вектор, идущий от начала полигона, составленного из векторов-слагаемых, к его концу (рис. 1.3).Сложение нескольких векторов может быть выполнено и последовательно (рис. 1.4 ).

Равнодействующую системы сходящихся сил можно определить и аналитически. Для этого выбирают систему координатных осей x и y , находят углы наклона каждой силы. Проекция равнодействующей на ось x равна алгебраической сумме проекций слагаемых сил на эту ось (рис.1.5)

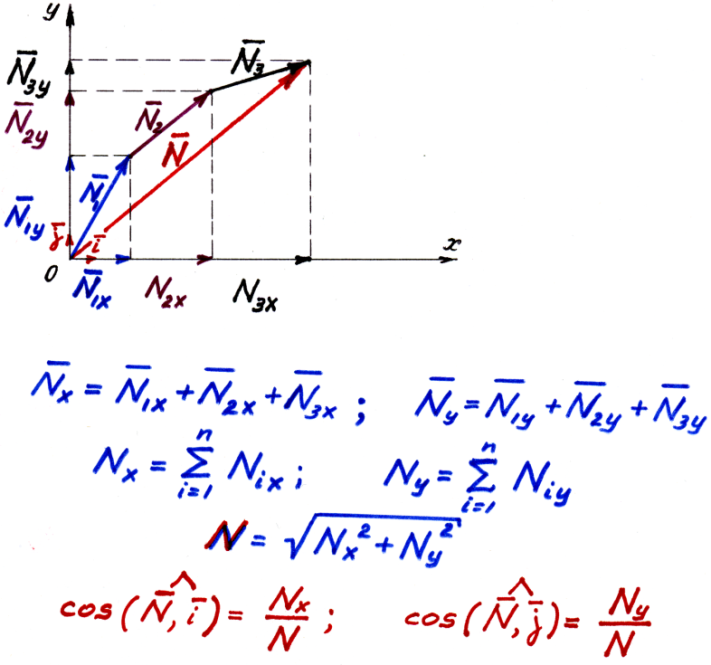
Рис. 1.3. Рис. 1.4. Рис.1.5.

.

Аналогично

Здесь n- число слагаемых векторов. Величина равнодействующей

Направляющие косинусы:

,

где i, j - единичные вектора в направлении оси x и y соответственно.

1.4 Равновесие системы сходящихся сил.

Если полигон векторов замыкается, то сумма векторов, его составляющих, равна нуль - вектору. И наоборот . Для того ,чтобы система сходящихся сил находилась в равновесии, необходимо и достаточно равенства нулю равнодействующей этой системы сил:

R=0.

Например, сумма сил (рис. 1,2, 1.6 ) из условия равновесия

.

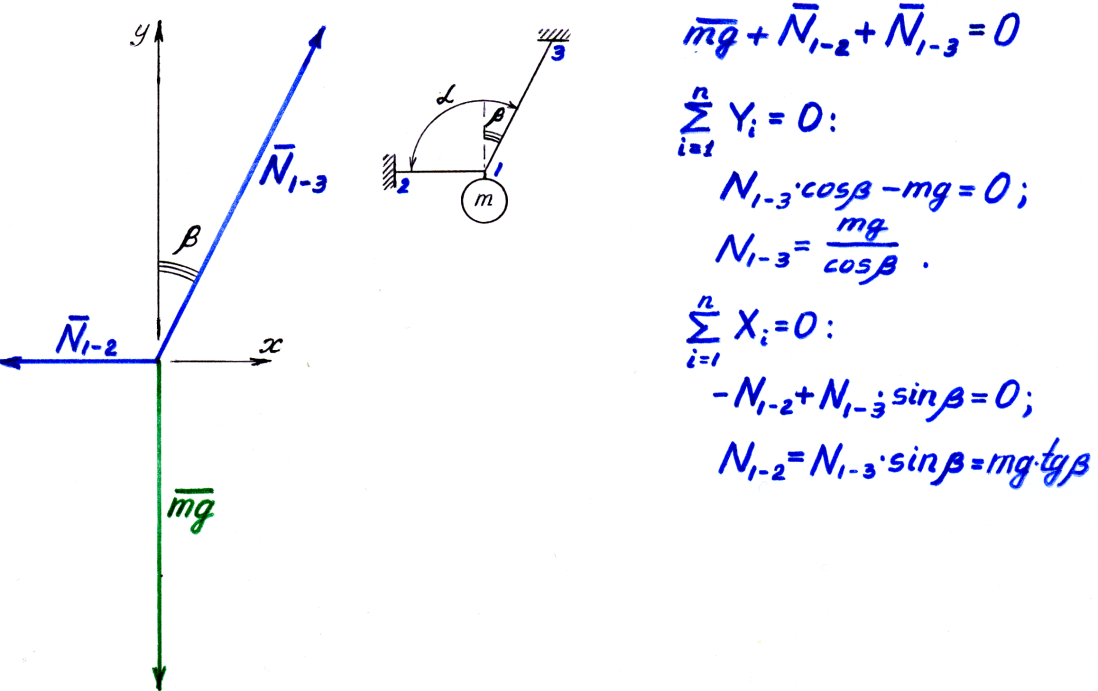
Рис.1.6.

В проекции на ось y при γ =:

В проекции на ось x:

Знаки « + » говорят о том, что предположение о том , что усилия и являются растягивающими, верны.

2. Плоская система произвольно расположенных сил.

2.1. Момент силы относительно точки.

а) б)

Рис.2.1.

На рис.2.1 ℓ-линия действия силы

О - моментная точка: точка, относительно которой необходимо определить момент,

h - плечо: кратчайшее расстояние от моментной точки до линии действия силы (длина перпендикуляра).

Для рис.2.1а (сила Р старается повернуть по часовой стрелке ):

M= +Рh .

Для рис.2.1б (вращение против часовой стрелки)

M= -Рh.

Моментом М силы относительно точки О называется взятое со знаком произведение силы на плечо:

.

С понятием момента силы мы встречаемся, открывая дверь, водопроводный кран, затягивая гайку гаечным ключом, вращая педали велосипеда и т.д.

Слишком большой момент силы не всегда полезен. Чтобы не сорвать резьбу, ограничивают длину гаечного ключа. При заданных длине и поперечном сечении стойки необходимо ограничить размер рекламного щита, чтобы при порывах ветра стойку не согнуло (рис2.2).

Рис.2.2.

2.2. Момент пары сил.

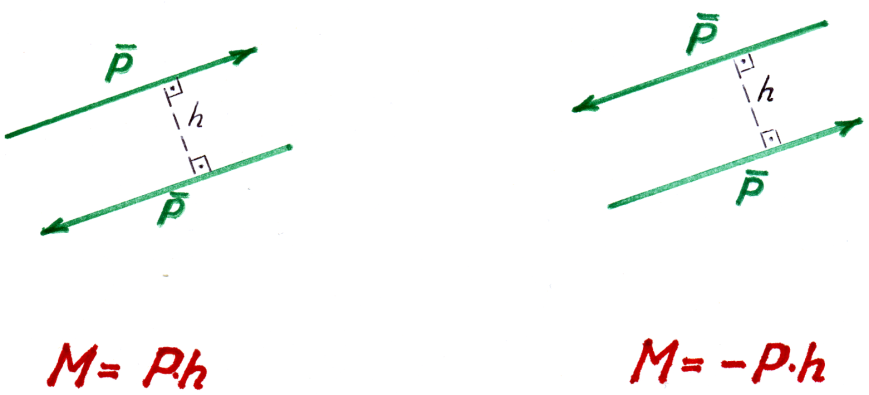
Рис.2.3.

Момент равных по величине, параллельных (колллинеарных), но с несовпадающими линиями действия противоположно направленных сил (рис. 2.3 )

,

где h- расстояние между линиями действиями сил (плечо пары).

2.3. Главный вектор. Главный момент.

Сложение сил, произвольно расположеных в плоскости, можно выполнить:

1. последовательным сложением;

2)приведением данной системы сил к произвольно выбранному центру.

Первый способ громоздок при большом количистве сил (а для пространственной неприменим).

Второй является общим и удобным.

Перенося все силы произвольно в точку О, называемую центром приведения, получим приложенную в этом центре силу:

и пару с моментом

Главный вектор системы сил- геометрическая сумма сил данной системы.

Главный момент плоской системы сил точки О- алгебраическая сумма мометов сил этой системы относительно точки О.