ЛЕКЦИЯ 5 альб

Лекция 5. Решение задач по теме "Аналитическая геометрия в пространстве"

1. Составить уравнение плоскости, проходящей через точку М₀(1, -2, 5) параллельно плоскости 7x-y-2z-1=0.

Решение. Обозначим через Р заданную плоскость, пусть Р₀ – искомая параллельная плоскость, проходящая через точку М₀(1, -2, 5).

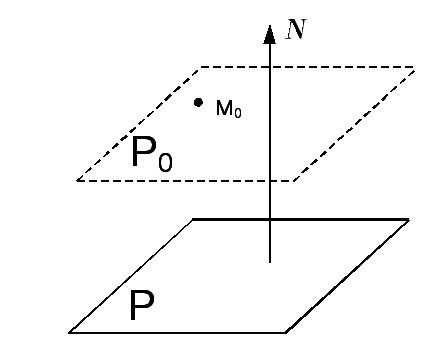
Рассмотрим нормальный (перпендикулярный) вектор плоскости Р. Координаты нормального вектора являются коэффициентами при переменных в уравнении плоскости  .

Поскольку плоскости Р и Р₀ параллельны, то вектор перпендикулярен плоскости Р₀, т.е. - нормальный вектор плоскости Р₀.

Уравнение плоскости, проходящей через точку М₀(x₀, y₀, z₀) с нормалью:

(1)

Подставляем координаты точки М₀ и вектора нормали в уравнение (1):

Раскрывая скобки, получаем общее уравнение плоскости (окончательный ответ):

.

2. Составить канонические и параметрические уравнения прямой, проходящей через точку М₀(-2, 3, 0) параллельно прямой .

Решение. Обозначим через L заданную прямую, пусть L₀ – искомая параллельная прямая, проходящая через точку М₀(-2,3,0).

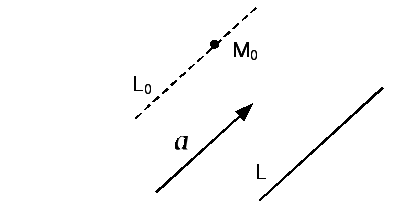
Направляющий вектор прямой L (ненулевой вектор, параллельный этой прямой) параллелен также и прямой L₀. Следовательно, вектор является направляющим вектором прямой L₀.

Координаты направляющего вектора равны соответствующим знаменателям в канонических уравнениях заданной прямой  .

Канонические уравнения прямой в пространстве, проходящей через точку M₀(x₀, y₀, z₀) параллельно ненулевому вектору {l, m, n}

. (2)

Подставляем координаты точки М₀ и направляющего вектора в уравнение (2) и получаем канонические уравнения прямой:

.

Параметрические уравнения прямой в пространстве, проходящей через точку M₀(x₀, y₀, z₀) параллельно ненулевому вектору {l, m, n}, имеют вид:

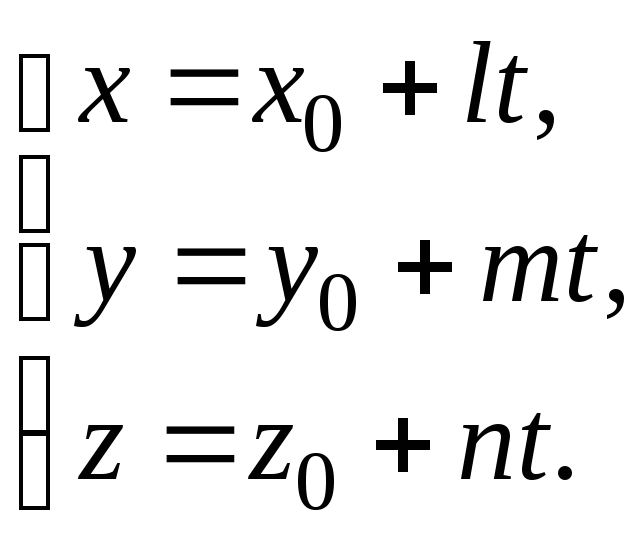(3)

Подставляем координаты точки М₀ и направляющего вектора в уравнения (3) и получаем параметрические уравнения прямой:

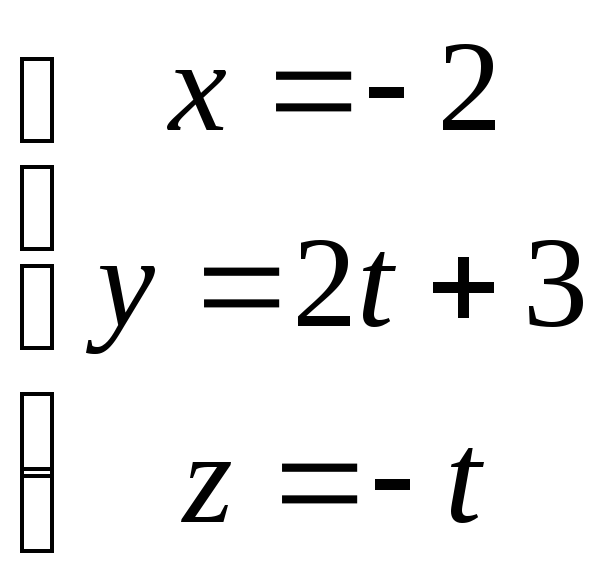
3. Найти точку , симметричную точке , относительно: а) прямой б) плоскости

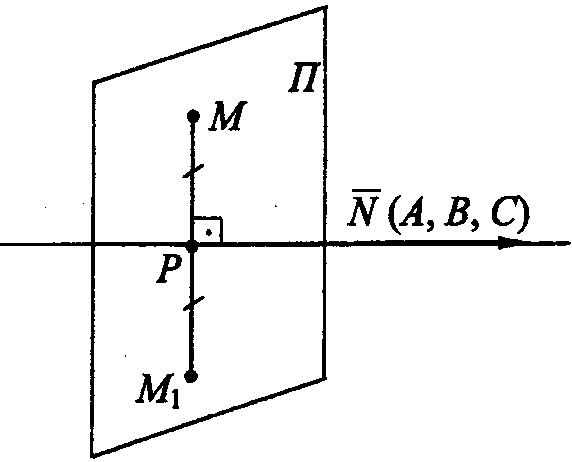
Решение. а) Составим уравнение перпендикулярной плоскости П, проектирующей точку на данную прямую:

Чтобы найти используем условие перпендикулярности заданной прямой и проектирующей плоскости. Направляющий вектор прямой перпендикулярен плоскости  вектор является вектором нормали к плоскости  Уравнение плоскости, перпендикулярной заданной прямой имеет вид или

Найдем проекцию Р точки М на прямую. Точка Р есть точка пересечения прямой и плоскости, т.е. ее координаты должны одновременно удовлетворять и уравнениям прямой, и уравнению плоскости. Решим систему:

.

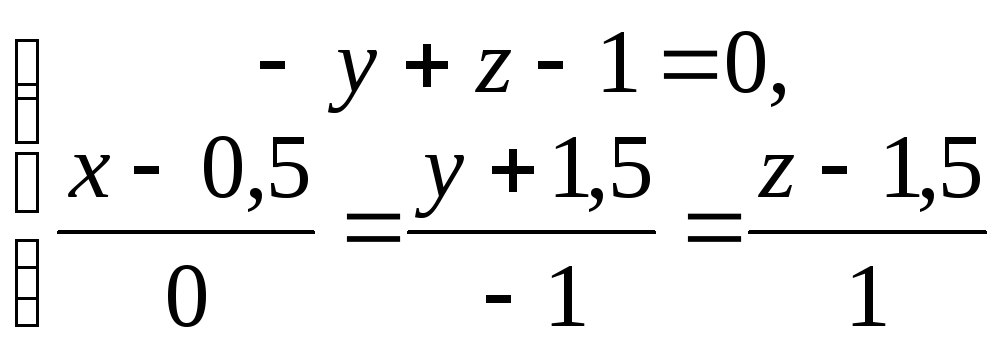Чтобы решить ее, запишем уравнение прямой в параметрическом виде:

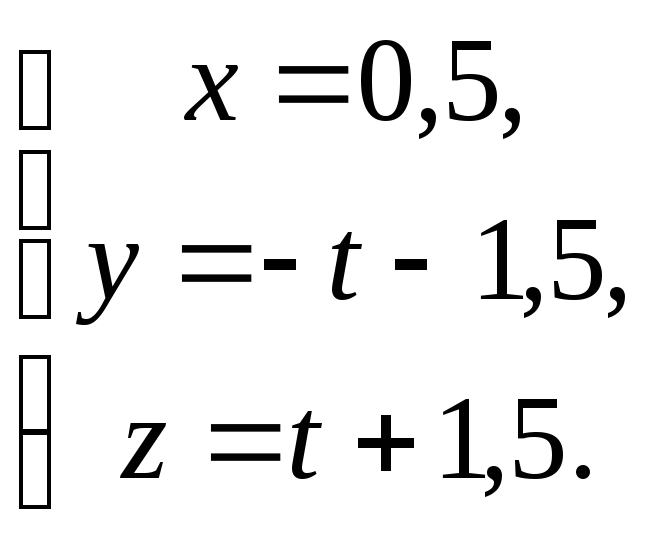
Подставляя выражения для в уравнение плоскости, получим:

Отсюда находим Найденные координаты – это координаты середины Р отрезка, соединяющего точку и симметричную ей точку

В школьном курсе геометрии формулировалась теорема.

Координаты середины отрезка равны полусуммам соответствующих координат его концов.

Находим координаты точки из формул для координат середины отрезка:

Получаем: Итак, .

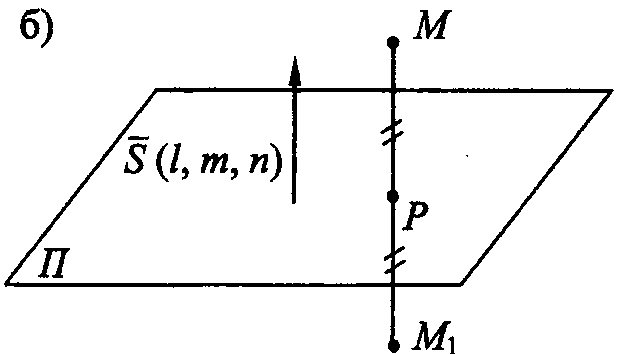
Решение. б) Чтобы найти точку, симметричную точке относительно данной плоскости П, опустим перпендикуляр из точки на эту плоскость. Составим уравнение прямой с направляющим вектором , проходящей через точку :

Перпендикулярность прямой и плоскости означает, что направляющий вектор прямой перпендикулярен плоскости  . Тогда уравнение прямой, проектирующей точку на заданную плоскость, имеет вид:

Решив совместно уравнения и найдем проекцию Р точки на плоскость. Для этого перепишем уравнения прямой в параметрическом виде:

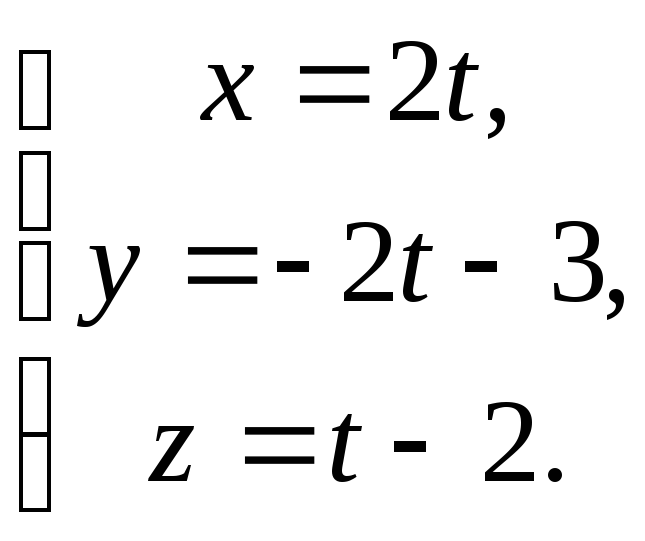
Подставим эти значения в уравнение плоскости: Аналогично п. а), используя формулы для координат середины отрезка, находим координаты симметричной точки :

т.е. .

4. Составить уравнение плоскости, проходящей а) через прямую параллельно вектору ; б) через две пересекающиеся прямые и (предварительно доказав, что они пересекаются); в) через две параллельные прямые и ; г) через прямую и точку .

Решение. а) Поскольку заданная прямая лежит в искомой плоскости, и искомая плоскость параллельна вектору , то нормальный вектор плоскости будет перпендикулярен направляющему вектору прямой и вектору .

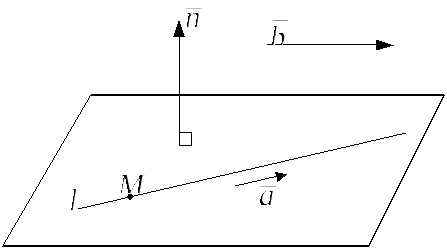
Следовательно, в качестве нормального вектора плоскости можно выбрать векторное произведение векторов и :

.

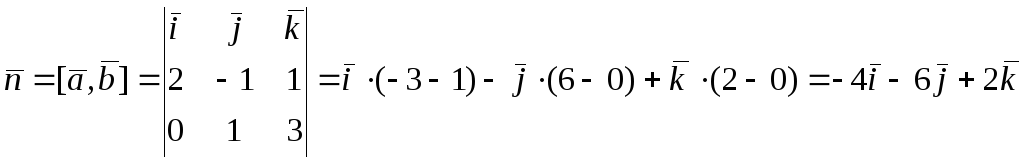Получаем координаты нормального вектора плоскости .

Найдем точку на прямой. Приравнивая отношения в канонических уравнениях прямой к нулю:

,

находим , , . Заданная прямая проходит через точку , следовательно, плоскость тоже проходит через точку . Используя уравнение плоскости, проходящей через заданную точку перпендикулярно вектору , получаем уравнение плоскости , или , или, окончательно, .

Решение. б) Две прямые в пространстве могут пересекаться, скрещиваться или быть параллельными. Заданные прямые

и (4)

не параллельны, поскольку их направляющие векторы и не коллинеарны: .

Как проверить, что прямые пересекаются? Можно решать систему (4) из 4 уравнений с 3 неизвестными. Если система имеет единственное решение, то мы получаем координаты точки пересечения прямых. Однако для решения нашей задачи - построения плоскости, в которой лежат обе прямые, точка их пересечения не нужна. Поэтому можно сформулировать условие пересечения двух непараллельных в пространстве прямых без нахождения точки пересечения.

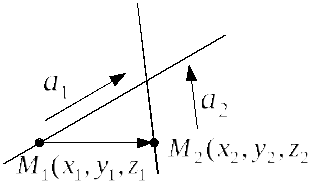
Если две непараллельные прямые пересекаются, то направляющие вектора , и соединяющий лежащие на прямых точки и вектор лежат в одной плоскости, т.е. компланарны  смешанное произведение этих векторов равно нулю:

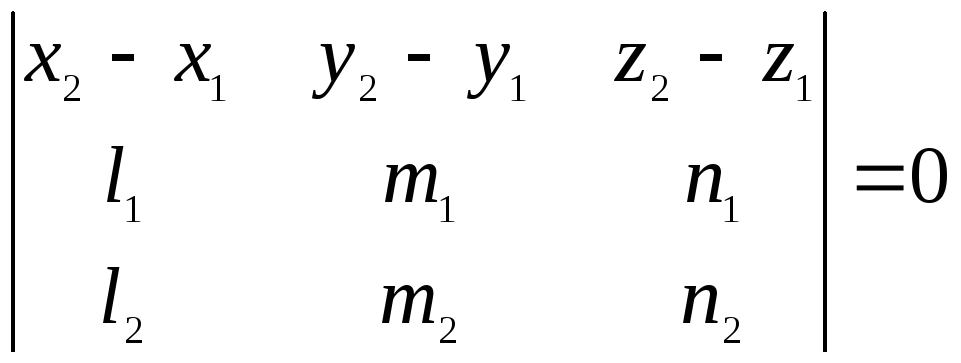. (5)

Приравниваем отношения в канонических уравнениях прямых к нулю (а можно к 1 или любому числу)

и ,

и находим координаты точек на прямых. Первая прямая проходит через точку , а вторая прямая – через точку . Направляющие векторы этих прямых соответственно равны и . Получаем

.

Равенство (5) выполнено, следовательно, заданные прямые пересекаются. Значит, существует единственная плоскость, проходящая через эти две прямые.

Переходим ко второй части задачи – составление уравнения плоскости.

В качестве нормального вектора плоскости можно выбрать векторное произведение их направляющих векторов и :

.

Координаты нормального вектора плоскости .

Мы выяснили, что прямая проходит через , следовательно, искомая плоскость тоже проходит через эту точку. Получаем уравнение плоскости , или или, окончательно, .

в) Так как прямые и параллельны, то в качестве нормального вектора нельзя выбрать векторное произведение их направляющих векторов, оно будет равно нулевому вектору.

Определим координаты точек и , через которые проходят эти прямые. Пусть и , тогда , . Вычислим координаты вектора . Вектор лежит в искомой плоскости и неколлинеарен вектору , тогда в качестве ее нормального вектора можно выбрать векторное произведение вектора и направляющего вектора первой прямой :

. Итак, .

Плоскость проходит через прямую , значит, она проходит через точку . Получаем уравнение плоскости: , или .

г) Приравнивая отношения в канонических уравнениях прямой к нулю , находим , , . Следовательно, прямая проходит через точку .

Вычислим координаты вектора . Вектор принадлежит искомой плоскости, в качестве ее нормального вектора выберем векторное произведение направляющего вектора прямой и вектора :

.

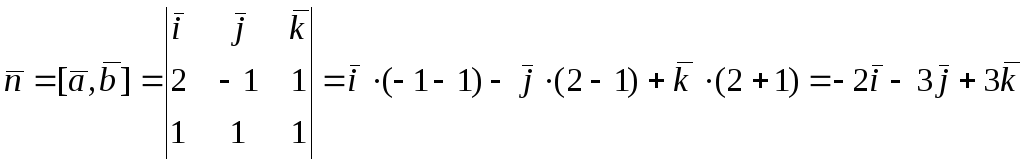Тогда уравнение плоскости имеет вид: , или .