
лекції по мат.логике / L2-tex
.pdf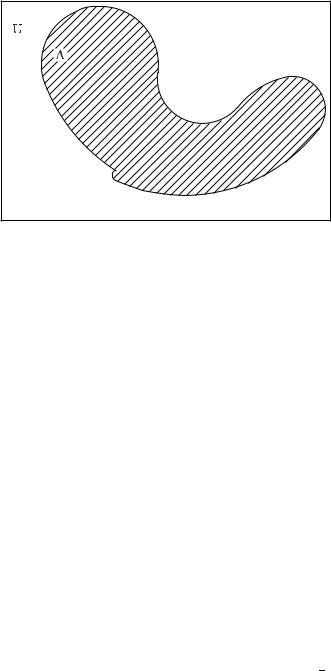
Рис. 2: Множина A задана дiаграмою Вена. Через U позначена унiвер- |
сальна множина |
Коли в мiркуваннях зустрiча¹ться унiверсальна множина, то ¨¨ зображають у виглядi прямокутника, всерединi якого розташовують круги чи iншi геометричнi фiгури, що зображають решту множин. Якщо одна множина ¹ пiдмножиною друго¨, то область, що зобража¹ першу множину, повинна розташовуватися всерединi областi, що зобража¹ другу. На вiдмiну вiд геометричних креслень, якi не приймаються в якостi доведення, мiркування з використання кругiв Ейлера чи дiаграм Вена вважаються переконливими.
3 Операцi¨ над пiдмножинами
Найбiльш важливi дi¨ над множинами це ¨х перетин (позна- ча¹ться знаком \), об'¹днання (познача¹ться через [), рiзниця
(познача¹ться знаком n) та симетрична рiзниця ¡. Äëÿ ñèìå-
трично¨ рiзницi вжива¹ться також позначення 4.
3.1 Об'¹днання пiдмножин
Об'¹днанням A [ B множини A та множини B назива¹ться множина
A [ B = fxjx 2 A àáî x 2 Bg:
11
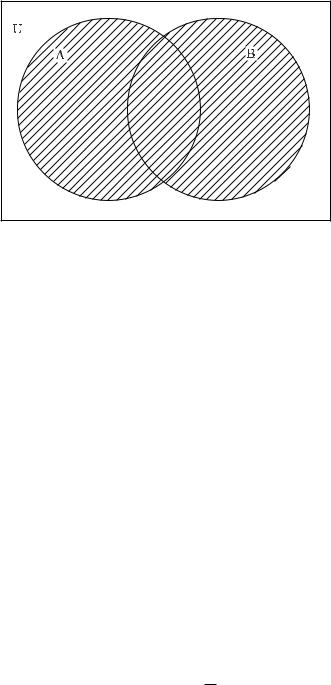
Тобто в об'¹днаннi двох множин лежать тi i тiльки тi елементи унверсально¨ множини, якi належать або першiй множинi або другiй.
Рис. 3: Заштриховано об'¹днання A [ B множин A òà B |
Çíàê [ - це стилiзована латинська буква U, що ¹ першою
буквою латинського слова unio , що означа¹ з'¹днувати . Так,
ÿêùî A = f1; 2; 3g; B = f2; 3; 4g; òî A [ B = f1; 2:3; 4g
Щоб одержати розв'язки рiвняння
f(x) ¢ g(x) = 0;
розв'язують два рiвняння
f(x) = 0; g(x) = 0;
одержують двi множини розв'язкiв, беруть об'¹днання одержаних множин i це буде вiдповiддю. Так для розв'язування рiвняння sin x ¢ cos x = 0 випису¹мо два рiвняння i випису¹мо
множини ¨х розв'язкiв:
sin x = 0; A = fxjx = ¼k; k 2 Zg; cos x = 0; B = fxjx = ¼2 + ¼k; k 2 Zg:
12

Кiнцева вiдповiдь одержу¹ться як об'¹днання одержаних множин розв'язкiв
A [ B = fxjx = ¼k2 ; k 2 Zg:
3.2 Перетин пiдмножин
Перетином A \B множини A та множини B назива¹ться мно-
æèíà
A \ B = fxjx 2 A i x 2 Bg:
Çíàê \ це перевернутий знак [: ßêùî
A = f1; 2; 3g; B = f2; 3; 4g;
òî
A \ B = f2; 3g:
ßêùî A - це множина книжок, що лежать на столi, а B - множина пiдручникiв, то A \ B це множина пiдручникiв, що
лежать па столi.
Розв'язком системи рiвнянь ¹ перетин множин розв'язкiв окремих рiвнянь. Для прикладу вiзьмемо систему
½2x ¡ y = 7;
5x + y = 21
Множина розв'язкiв першого рiвняння склада¹ться iз усiх то- чок прямо¨, що ма¹ рiвняння y = 2x ¡ 7: Множина розв'язкiв
другого рiвняння склада¹ться iз усiх точок прямо¨, що ма¹ рiвняння y = ¡5x + 21: Перетином цих двох прямих ¹ точка з ко-
ординатами (4,1). Отже розв'язком системи буде x = 4; y = 1:
Також множина розв'язкiв системи нерiвностей ¹ перетином множин розв'язкiв окремих нерiвностей, що входять у систему.
Областю визначення суми двох функцiй ¹ перетин областей визначення доданкiв. Оскiльки функцiя ln x визначена
13
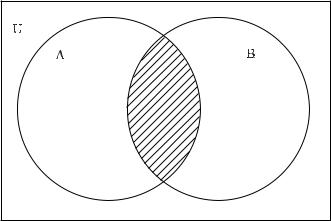
Рис. 4: Заштриховано перетин A [ B множин A òà B
при додатних значеннях x, а функцiя arcsin x визначена при ¡1 · x · 1; то областю визначення функцi¨
f(x) = ln x + arcsin x
буде множина 0 < x · 1:
ßêùî A µ B; то спiльними для A i B будуть елементи iз A i òiëüêè âîíè. Òîìó A \ B = A. Оскiльки елементiв iз А, що
не лежать в В нема¹, то A [ B = B: За допомогою логiчно¨ символiки сказане можна записати так:
A µ B ) A \ B = A;
A µ B ) A [ B = B:
Зворотнi iмплiкацi¨
A µ B ( A \ B = A;
A µ B ( A [ B = B:
також правильнi.
Iз визначення операцiй перетину та об'¹днання видно, що
; \ A = ;; ; [ A = A:
14
для будь-яко¨ множини A, i
U \ A = A; U [ A = U
для будь-яко¨ множини А i унiверсально¨ множини U . |
|
Оскiльки кожен елемент, що лежить в A \ B; одночасно |
|
лежить i в A i â B, òî |
|
A \ B µ A; |
A \ B µ B: |
Також правильними ¹ включення |
|
A [ B ¶ A; |
A [ B ¶ B: |
3.3 Рiзниця та симетрична рiзниця пiдмножин
Наступнi дi¨ це рiзниця, симетрична рiзниця двох множин та доповнення.
Рiзницею A n B множини A i множини B (÷èòà¹òüñÿ ÿê A áåç B) назива¹ться множина
A n B = fxj(x 2 A) ^ (x 2= B)g:
Наприклад, коли A = f1; 2; 3g; à B = f2; 3; 4g; òî
A n B = f1g
i
B n A = f4g:
Êîëè A µ B, тодi елементiв, для яких x 2 A i x 2= B, íå
iñíó¹ , òîìó A n B = ;: Логiчною символiкою сказане можна записати так:
A µ B ) A n B = ;:
Зворотна iмплiкацiя
A µ B ( A n B = ;
15
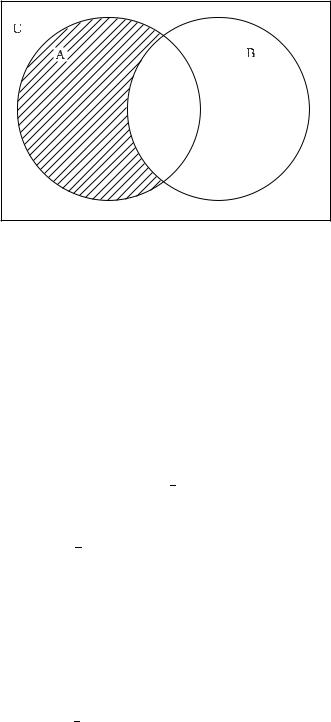
Рис. 5: Заштрихована рiзниця A n B множин A i B.
також правильна, тому що вона означа¹ наступне: коли елементiв, якi лежать в A i не лежать в B нема¹, тодi всi елементи
iç A лежать в B .
Множини AnB i B nA спiвпадають лише в одному випадку - коли спiвпадають самi множини A i B, - в цьому випадку
A n B = B n A = ;:
Симетричною рiзницею A¡B множин A òà B назива¹ться множина
A¡B = (A n B) [ (B n A):
Ця множина склада¹ться з тих елементiв першо¨ множини, що не лежать в другiй, i тих елементiв друго¨ множини, що не лежать в першiй. Таким чином, викинувши iз об'¹днання A [ B множин A i B ñïiëüíi äëÿ A i B елементи ми одержимо
симетричну рiзницю, тобто можна написати
A¡B = (A [ B) n (A \ B):
Наведемо приклад. Для
A = fn 2 Njn < 10g = f1; 2; 3; 4; 5; 6; 7; 8; 9g;
16

Рис. 6: Заштрихована симетрична рiзниця A¡B множин A i B. |
B = fn 2 Njn просте число, 1 < n < 20g = f2; 3; 5; 7; 11; 13; 17; 19g |
áóäå
A n B = f1; 4; 6; 8; 9g
i
B n A = f11; 13; 17; 19g:
Òîìó
A¡B = f1; 4; 6; 8; 9g[f11; 13; 17; 19g = f1; 4; 6; 8; 9; 10; 11; 13; 17; 19g:
У визначеннi симетрично¨ рiзницi множини A òà B рiвноправ-
нi, не ма¹ значення, яка з них розгляда¹ться першою, а яка другою. Тому
A¡B = B¡A
для будь-яких множин A i B.
ßêùî A¡B = ;; то порожньою ¹ i множина A n B i множина B n A: Це можливо лише за умови, що кожен елемент множини A ¹ елементом множини B i кожен елемент множи-
íè B ¹ елементом множини A, тобто коли A = B: Символьно сказане запису¹ться так:
A¡B = ; , A = B:
17

3.4 Доповнення
Рiзниця U n A мiж унiверсальною множиною U i заданою множиною A назива¹ться доповненням A i познача¹ться через ¡A.
Iнколи доповнення множини A познача¹ться A àáî C(A).
Коли ¹ сумнiв щодо унiверсально¨ множини (нагада¹мо, що унiверсальна множина частiше всього вгаду¹ться iз оточуючих мiркувань, iз контексту), тодi потрiбно вказати, з яких елементiв склада¹ться множина U, i говорити про доповнення A äî
U.
Наведемо приклади.
Якщо унiверсальна множина це множина книжок, а A це множина пiдручникiв, то ¡A - це множина книжок, що не
¹ пiдручниками.
ßêùî U - це множина цiлих чисел вiд 1 до 10, i A = f2; 3; 5; 6g,
òî ¡A = f1; 4; 7; 8; 9; 10g:
Область визначення функцi¨ часто задають як доповнення тi¹¨ множини чисел, на яких функцiя не визначена. Для прикладу, для знаходежння областi визначення функцi¨ f(x) =
(x2 ¡3x+2)¡1 ми знаходимо розв'язки рiвняння x2 ¡x+2 = 0; (íèìè ¹ x = 1; x = 2); i потiм область A визначення функцi¨ f(x) зада¹мо як доповнення множини B = f1; 2g :
A = ¡B = fxjx 6= 1 i x =6 2g:
3.5 Теоретико-множиннi тотожностi та ¨х доведення.
Випишемо основнi тотожностi, якi виконуються для теоретикомножинних операцiй.
A [ A = A; A \ A = A закони iдемпотентпостi для об'¹днання та перетину.
18
Рис. 7: Заштрихована доповнення мнжини A. |
A [ B = B [ A; A \ B = B \ A закони комутативностi
для об'¹днання та перетину.
(A [ B) [ C = A [ (B [ C); (A \ B) \ C = A \ (B \ C)
закони асоцiативностi для об'¹днання та перетину.
(A [ B) \ C = (A \ C) [ (B \ C); (A \ B) [ C = (A [
B) \ (B [ C) два дистрибутивнi закони для об'¹днання та
перетину. |
|
A [ (A \ B) = A; A \ (A [ B) = A закони поглинання. |
|
A [ U = U; |
A \ U = A властивiсть унiверсально¨ мно- |
æèíè. |
A [ ; = A властивiсть порожньо¨ множини. |
A \ ; = ;; |
|
Доведення цих тотожностей проводиться або з допомогою кругiв Ейлера. або з вказiвкою на особливостi вжитку математиками сполучникiв, особливостi оцiнки математиками правильностi сказаного в складних реченнях. Так, закон iдемпотеитностi для об'¹днання A [A = A об рунтову¹ться специфi-
кою розумiння математиками сполучника i : сказане в складному реченнi Елемент x належить множинi A i елемент x
належить множинi A правильне тодi i тiльки тодi, коли правильне просте речення Елемент x належить множинi A .
19

Закони дистрибутивностi простiше доводити за допомогою кругiв Ейлера.
Вкажемо декiлька тотожностей, що стосуються рiзницi, симетрично¨ рiзницi та доповнення.
1. A n ; = A; U n A = ¡A; A n A = ;:
2. ¡(A\B) = (¡A)[(¡B); ¡([B) = (¡A)\(¡B) öi äâi
тотожностi часто використовуються i мають спецiальну назву - закони де Моргана.
3. |
A n (B [ C) = (A n B) \ (A n C); A n (B \ C) = (A n B) [ |
|
(A n C): |
4. |
An(B nC) = (AnB)[(A\C); (AnB)nC = An(B [C): |
5. |
A¡(B¡C) = (A¡B)¡C; A\(B¡C) = (A\B)¡(A\C): |
6. |
A¡(A¡B) = A \ B: |
В геометрi¨ часто унiверсальною множиною ¹ множина то- чок, прямих i площин в тривимiрному просторi. Таким чином деякi елементи унверсально¨ множини можуть вiдрiзнятися один вiд одного вельми сутт¹во. В такому випадку вижавають термiн багатосортна множина . Отже,
багатосортна множина ¹ об'¹днанням певних пiдмножин, що не мають спiльних елементiв.
4 Обмеженi квантори
В мiркуваннях, що стосуються багатосортних множин, загальнi квантори практично не використовуються використовуються так званi обмеженi квантори.
Такi словосполуки як iсну¹ елемент в множинi тадля всiх елементiв множини називають обмеженими кванторами.
20
