
лекції по мат.логике / L5-funct
.pdfВiдношення та вiдображення. Дi¨ з ними
Григорiй Чарльзович Курiнний Жовтень, 2010
Çìiñò
1 |
Декартовий степiнь множини, вiдношення, вiдображення, фун- |
|
|||
|
êöiÿ. |
|
|
1 |
|
|
1.1 |
Декартовий добуток. Декартовий квадрат. |
. . . . . . . . . . . . . . |
1 |
|
|
1.2 |
Вiдповiдностi та вiдношення . . . . . . . |
. . . . . . . . . . . . . . . |
2 |
|
2 |
Вiдображення та функцi¨ |
|
4 |
||
|
2.1 |
Всюди визначенi та частковi вiдображення . . . . . . . . . . . . . . |
4 |
||
|
2.2 |
Способи задання вiдображення . . . . . . . . . . . . . . . . . . . . . |
5 |
||
|
2.3 |
Типи вiдображень . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
6 |
||
|
2.4 |
n¡й декартовий степiнь множини, n¡мiснi функцi¨, n¡ìiñíi âiä- |
|
||
|
|
ношення . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
8 |
||
|
2.5 |
Вiдображення i послiдовностi . . . . . . . . . . . . . . . . . . . . . . |
9 |
||
3 |
Композицiя вiдображень та вiдношень. |
|
10 |
||
|
3.1 |
Складна функцiя. . . |
. . . . . . . . . . . . . . . . . . . . . . . . . . |
10 |
|
|
3.2 |
Композицiя вiдношень. |
. . . . . . . . . . . . . . . . . . . . . . . . . |
10 |
|
|
3.3 |
Властивостi композицi¨ вiдображень . . . . . . . . . . . . . . . . . . |
12 |
||
|
3.4 |
Вправа знайти композицiю двох функцiй . . . . . . . . . . . . . |
14 |
||
|
3.5 |
Оберненi вiдображення . . . . . . . . . . . . . . . . . . . . . . . . . |
16 |
||
4 |
Основнi числовi функцi¨. |
|
18 |
||
1Декартовий степiнь множини, вiдношення, вiдображення, функцiя.
1.1 Декартовий добуток. Декартовий квадрат.
Вважа¹мо зрозумiлим, що таке впорядкована пара i невпорядкована. Коли ма¹мо 21 десятковий запис числа двадцять один, i 12 десятковий запис числа
1
дванадцять, то порядок запису цифр в записах сутт¹вий, тому кажемо, що в даному випадку пара цифр 12 пара цифр 21 впорядкованi, тобто порядок запису елементiв (в даному разi цифр) сутт¹вий. Коли ж ми ма¹мо яблуко i грушу, або ма¹мо ту ж грушу i те ж яблуко, то порядок ¨х перерахування несутт¹вий. В цьому розi кажемо про невпорядковану пару {яблуко, груша}.
ßêùî A; B двi множини, i a 2 A; b 2 B; òî (a; b) впорядкована пара, (a; b) =6 (b; a) ïðè a =6 b: А для невпорядковано¨ пари fa; bg завжди викону¹ться рiвнiсть fa; bg = fb; ag: Подiбним чином розгляда¹мо впорядкованi послiдовностi
(a1; a2; : : : ; an); a1 2 A1; a2 2 A2; : : : an 2 An:
Впорядкованi послiдовностi називають також кортежами та векторами.
Для будь-яких множин A; B можна розглядати множину всiх впорядкованих пар f(a; b)ja 2 A; b 2 Bg: Ця множина назива¹ться декартовим або прямим добутком множин A i B i познача¹ться A £ B:
Äëÿ A = f1; 2g; B = fx; y; zg
A £ B = f(1; x); (1; y); (1; z); (2; x); (2; y); (2; z)g;
A £ A = A2 = f(1; 1); (1; 2); (2; 1); (2; 2)g:
Декартовий добуток порожньо¨ множини на будь-яку множину буде порожньою множиною. Це твердження доводиться методом вiд протилежного. Дiйсно, нехай A = ;, B деяка множина, i C = A £ B. ßêùî C не порожня
множина, то в нiй iсну¹ якийсь елемент припустимо c 2 C: За визначенням прямого добутку для деяких a 2 A; b 2 B áóäå c = (a; b). Оскiльки ми вказали елемент a 2 A; òî A не порожня множина, що суперечить припущенню.
Декартовий добуток множини на себе називають декартовим квадратом множини.
Можна розглядати декартовий добуток порожньо¨ множини множникiв, декартовий добуток одного множника, декартовий добуток дтрьо¨ множникiв i т.п. Подiбним чином, можна розглядати нульовий степiнь множини, перший стапiнь множини, третiй степiнь множини i т. п. Цi конструкцi¨ розглядаються в наступних лекцiях.
1.2 Вiдповiдностi та вiдношення
Пiдмножини декартового добутку двох множин називають вiдповiдностями,
пiдмножини декартового квадрату називають бiнарними вiдношеннями.
2

56 |
|
56 |
4 |
|
4 |
3 |
|
3 |
2 |
|
2 |
1 |
|
1 |
1 |
2 -3 |
1 2 -3 |
|
|
Рис. 1: Прямим добутком вiдрiзка [1; 2] íà âiä- Рис. 2: Прямим добутком вiдрiзка [1; 3] íà âiä- ðiçîê [2; 5] ¹ прямокутник ðiçîê [2; 3] ¹ прямокутник.
56 |
56 |
4 |
4 |
3 |
3 |
2 |
2 |
1 |
1 |
1 2 -3 |
1 2 -3 |
Рис. 3: Прямим добутком вiдрiзка |
[1; 3] íà Рис. 4: Прямим добутком двоелеметно¨ мно- |
чотириелеметну множину f2; 3; 4; 5g ¹ чотири жини f1; 3g на двоелеметну множину f2; 5g ¹ |
|
âiäðiçêè |
чотири точки. |
3

ßêùî A = f4; ¤; ?; rg à B = f1; 2; 3; 4; 5g, òî |
|
C = f(4; 2); (¤; 5); (?; 1); (r; 3) |
(1) |
âiäïîâiäíiñòü ìiæ A òà B, яка задана перелiком сво¨х елементiв, а |
|
D = f(4; 4); (¤; ¤); (?; ?); (r; r)g |
(2) |
¹ вiдношенням на множинi A.
Нагада¹мо, що предикат i його область iстинностi можна не розрiзняти, побiдно до того, як iнколи можна не розрiзняти функцiю та ¨¨ графiк. Це нагадування викликано тим, що вiдношення ми уже згадували, коли говорили про n¡ìiñíi
предикати.
На рис. 1, 1,1,1 заданi 4 вiдношення на множинi дiйсних чисел. ˆх, вiдповiдно, можна задати iншим чином, наприклад
px ¡ 1 ¢ p2 ¡ x ¢ py ¡ 2 ¢ p5 ¡ y = p(x ¡ 1)(2 ¡ x)(y ¡ 2)(5 ¡ y);
px ¡ 1 ¢ p3 ¡ x ¢ py ¡ 2 ¢ p¡y = p(x ¡ 1)(3 ¡ x)(y ¡ 2)(3 ¡ y); px ¡ 1 ¢ p3 ¡ x + (y ¡ 2) ¢ (y ¡ 3) ¢ (y ¡ 4) ¢ (y ¡ 5) = p(x ¡ 1)(3 ¡ x);
((x ¡ 1)2 + (y ¡ 2)2) ¢ ((x ¡ 1)2 + (y ¡ 5)2)¢
¢ ((x ¡ 3)2 + (y ¡ 2)2) ¢ ((x ¡ 3)2 + (y ¡ 5)2) = 0: (3)
2 Вiдображення та функцi¨
2.1 Всюди визначенi та частковi вiдображення
Нехай A; B двi множини i f µ A £ B вiдповiднiсть. Якщо для кожного елемента a 2 A iсну¹ i до того ж ¹диний елемент b 2 B такий, що (a; b) 2 f, òîäi âiäïîâiäíiñòü f називають вiдображенням iз множини A в множину B i пишуть f : A ! B.
Елемент b 2 B такий, що (a; b) 2 f позначають f(a), називають образом
f
елемента a i пишуть b = f(a) òà a 7!b. Множину B1 = fb 2 Bj(a; b) 2 f для деякого a 2 Ag називають областю значень вiдображення f àáî
образом множини A при вiдображеннi f i позначають B1 = f(A):
Âiäïîâiäíiñòü C мiж множинами A = f4; ¤; ?; rg òà B = f1; 2; 3; 4; 5g, яка задана перелiком (1) ¹ вiдображенням. Вiдповiдно, можна писати
C : A ! B; 4 7!2; ¤ 7!5; ? 7!1; r 7!3:
4

Також можна писати |
C |
|
|
|
C(4) = 2; ¤ 7!5: |
Образом елемента ? 2 A ¹ 1. Образом всi¹¨ множини A ¹ множина f1; 2; 3; 5g: Iнколи виника¹ потреба розглядати випадки f µ A £ B, коли для кожного
елемента a 2 A iсну¹ не бiльше одного елемента b 2 B такого, що (a; b) 2 f, òîäi âiäïîâiäíiñòü f називають частковим вiдображенням iз множини A в множину B, або не всюди визначеним вiдображенням iз множини A в множину B. В такому випадку множину fa 2 Aj(a; b) 2 fb 2 Bg називають областю визначення вiдображеня f.
¼ |
У вiдповiдностi до сказаного, tg x ¹ вiдображенням iз множини fx 2 Rjx 6= |
2 |
+ k¼ для деякого k 2 Zg у множину R.  òîé æå ÷àñ tg x ¹ частковим вiдобра- |
женням iз множини R у множину R.
Вiдображення з рiзними областями визначення обов'язково рiзнi.
Коли виника¹ потреба пiдкреслити що для кожного елемента a 2 A iñíó¹
елемент b 2 B такий, що (a; b) 2 f, тодi вiдображення f називають всюди визна-
ченим. p Функцiя sin x всюди визначена на множинi дiйсних чисел, а функцiя x ¹ ÷àñ-
тковою функцi¹ю на множинi дiйснихpчисел,pàëå ¹ всюди визначеною на множинi невiд'¹мних дiйсних чисел. Функцi¨ x òà jxj ¹ рiзними функцiями.
Два вiдобрження збiгаються (це одне i те ж вiдображення, це рiвнi вiдображення) в тому i тiльки тому випадку, коли цi два вiдображення заданi на однiй i тiй же множинi, мають одну i ту ж область визначення i значення вiдображень на будь-якому елементi iз областi визначення збiгаються.
2.2 Способи задання вiдображення
Мовна практика дозволя¹ не розрiзняти вiдображення та спосiб його заданняалгоритмом, аналiтично (формулою), графiчно, таблично, чи в iнший спосiб. Проте варто пам'ятати, що рiзнi формули, рiзнi таблицi, рiзнi алгоритми можуть задавати одне i те ж вiдображення.
Для числових функцiй поширеним ¹ аналiтичне задання задання у виглядi формул, якi використовують певний набiр вiдомих функцiй. Так аналiтично заданими функцiями будуть
f1(x) = 5x3 ¡ 7x + 9 многочлен, цiла функцiя;
7x4 ¡ 3x3 + 11
x ¡ 2 рацiональна функцiя; f3 = sin 2x ¡ 5 cos x тригонометрична функцiя.
Для показу на екранi для великого загалу людей використовують графiчне задання функцiй графiки, тi чи iншi гiстограми (див. рис. 5,2.2)
5
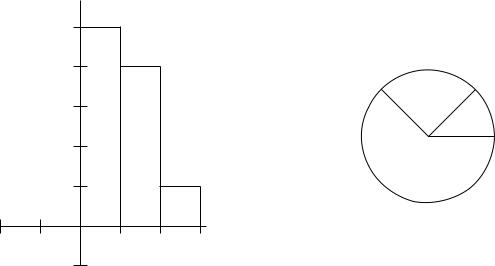
56
4
3
2
1
2008 2009 2010-
Рис. 5: Приклад стовпчиково¨ гiстограми
25%
13%
62%
Рис. 6: Приклад кругово¨ гiстограми.
Для задання вiдображення iз скiнченно¨ множини A в скiнченну множину B
часто використовують табличне задання, задання двома рядками. У верхньому рядку виписують всi елементи (для всюди визначено¨ функцi¨) або частину елементiв (для частково¨ фукнцi¨) множини A. нижньому рядку виписують образи
вiдповiдних образи вiдповiдних елементiв. Табличка береться в круглi дужки. |
||||||||||||
Так вiдображення (1) можна задати таблицею |
¶ |
|
|
|
||||||||
|
|
|
µ |
2 |
|
5 |
1 |
3 |
|
|
|
|
|
C = |
|
4 ¤ ? |
r |
|
: |
|
|
||||
Для вiдображення |
µ |
|
|
|
|
|
|
|
|
|
¶: |
|
f = |
7 |
5 |
1 |
3 |
9 |
2 |
4 |
8 |
6 |
(4) |
||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
можна написати f(5) = 9; f(9) = 6: У верхньому рядку такого табличного задан-
ня функцi¨ (задання двома рядками) обов'язково всi елементи рiзнi. У нижньому рядку елементи можуть бути однаковi.
2.3 Типи вiдображень
ßêùî f(A) = B, то вiдображення f : A ! B називають сюр'¹ктивним.
Для сюр'¹ктивних вiдображень вживають також назву вiдображення на та накладання .
Вiдображення sin x iз множини дiйсних чисел у вiдрiзок [¡1; 1] ¹ сюр'¹ктивним, тому що для будь-якого числа ¡1 · y · 1 iсну¹ число x, à ñàìå x = arcsin y, образом якого пiд дi¹ю вiдображення синус буде y.
6

Вiдображення sin x iз множини дiйсних чисел у множину дiйсних чисел не ¹
сюр'¹ктивним, тому що число 8 не ¹ образом жодного числа.
Вiдображення C в прикладi (1) не ¹ сюр'¹ктивним, тому що 4 не ¹ образом жодного елемента iз A.
ßêùî 8a1; a2 2 A(a1 6= a2 ) f(a1) =6 f(a2), то вiдображення f : A ! B
називають iн'¹ктивним. Для iн'¹ктивних вiдображень вживають також назву вiдображення в та вкладання
Вiдображення C в прикладi (1) ¹ iн'¹ктивним, тому що жоден iз елементiв множини B не ма¹ двох прообразiв iз A.
Вiдображення y = x2 iз множини дiйсних чисел у множину дiйсних чисел не
¹ нi сюр'¹ктивним нi iн'¹ктивним. Не сюр'¹ктивним воно ¹ тому, що число -1 не ма¹ прообразу, а не iн'¹ктивним тому, що число 1 ма¹ два прообрази 1 та -1.
Якщо вiдображення i iн'ктивне i сюр'¹ктивне, то його називають бi¹ктивним або вза¹мно однозначним. Вза¹мно однозначне вiдображення iз скiнченно¨ множини в себе називають пiдстановками.
Нехай ма¹мо вiдображення f : A ! B i f(a) = b для деяих елементiв a 2 A; b 2 B. Нагада¹мо, що тодi b ¹ образом елемента a, а елемент a ¹ прообразом елемента b.
Повний прообраз елемента b це множина всiх його прообразiв:
f¡1(b) = fa 2 Ajf(a) = bg:
Повний прообраз пiдмножини C ½ B öå
f¡1(C) = [ f¡1(x):
x2C
Таким чином, коли розгляда¹ться функцiя sin x на множинi дiйсних чисел, то
повний прообраз елемента 1
2 це множина чисел, якi множна записати у виглядi
¼6 + (¡1)nn¼
для деякого цiлого числа n. А повний прообраз числа 2 порожнiй.
Для вiдображення x 7!x2 повний прообраз нуля склада¹ться лише iз нуля,
повний прообраз числа 4 двоелементний склада¹ться iз чисел 2 та -2, а повний прообраз кожного вiд'¹много числа порожнiй.
Запропонована термiнологiя дозволя¹ сказати, що вiдображення f : A ! B ¹
² iн'ктивним, коли рiзнi елементи iз A мають рiзнi образи;
7
²сюр'¹ктивним, коли кожен елемент iз B ма¹ прообраз.
²вза¹мно однозначним, коли кожен елемент iз B ма¹ ¹диний прообраз.
ßêùî B пiдмножина множини A, то вiдображення f : B ! A f(x) = x ¹ канонiчним iн'¹ктивним вiдображенням iз пiдмножини в множину.
Отже при канонiчному вкладаннi цiлих чисел в дiйснi числа образом числа 5 буде 5, образом числа -7 буде -7, прообраз числа ¼ порожнiй.
Канонiчне вкладання f множини f2; 3; 5; 7g у множину f1; 2; 3; 4; 5; 6; 7; 8g ìî-
жна записати у виглядi |
µ |
2 |
3 |
5 |
7 |
¶: |
|
||||||
|
|
2 |
3 |
5 |
7 |
|
Вiдображення iз множини в числову множину називають функцi¹ю. Якщо B пiдмножина множини A, то вiдображення f : A ! f0; 1g
f(x) = 1; ÿêùî x 2 B i f(x) = 0; ÿêùî x 2= B називають характеристи- чною функцi¹ю пiдмножини.
Отже синус, косинус, показникова функцiя, степенева функцiя все це функцi¨. Характеристична функцiя пiдмножини f¡1; 1g множини дiйсних чисел ма¹
вигляд
f(x) = |
8 |
1; |
êîëè x = 1; |
|
|
< |
1; |
êîëè x = ¡1; |
|
|
0; |
êîëè x = |
1; 1 : |
|
|
: |
|
2 f¡ |
g |
Особливою пiдмножиною декартового квадрата непорожньо¨ множини A ¹
пiдмножина, що склада¹ться iз таких пар, де перший елемент пари збiга¹ться iз другим. Цю пiдножину називають дiагоналлю множини i позначають ¢A. ßêùî
цю пiдмножину називають вiдношенням, то це вiдношення рiвностi =. Ця ж пiдмножина може розглядатися як вiдображення, тодi це вiдображення називають тотожним i позначають idA:
¢A = f(a; a)ja 2 Ag; 8x 2 A(id(x) = x):
2.4 n¡й декартовий степiнь множини, n¡мiснi функцi¨, n¡мiснi вiдношення
n¡ий декартовий степiнь множини A n ¸ 1 склада¹ться iз послiдовно-
стей довжини n 2 N (a1; a2; : : : ; an), елементи яких лежать в A. Òàêi
послiдовностi в деяких контекстах (мовних оточеннях) називають словами в алфавiтi A. Будь-який додатний декартовий степiнь порожньо¨
множини ¹ порожньою множиною. Нульовий степiнь будь-яко¨ можини
8

(в тому числi i порожньо¨) одноелементний, елементом цього степеня ¹ порожня множина. Перший степiнь будь-яко¨ множини збiга¹ться з цi¹ю множиною.
Згiдно означення
p
(3; 2; 3; 7; 11) 2 N5; (¡3; 5; ¡7) 2 Z3; (01110111000) 2 f01g11; 3 2 R = R1:
n¡й декартовий степiнь множини A (n ¸ 0) познача¹ться An.
Якщо множина A числова, то вiдображення iз An â A назива¹ться n¡мiсною функцi¹ю, функцi¹ю вiд n çìiííèõ. Îòæå
y = (x1; x2; x3; x4) = 5x1 ¡ 3x2 + 7x4 + 11
це чотиримiсна функцiя, функцiя вiд 4 змiнних.
ßêùî n = 0, òî An = f;g i вiдображення f : An ! A може бути задане ¹диним сво¨м значенням f(;) 2 A: Тому кажуть, що функцiя вiд порожньо¨ множини змiнних це видiлене число. Звiдси виплива¹, що n-мiсних функцiй n = 0 на порожнiй множинi не iсну¹, а n-мiсна функцiя n ¸ 1 на порожнiй множинi ¹дина це порожня множина. Якщо вiдображення f : An ! A обчислю¹ться
вiд послiдовностi (a1; a2; : : : ; an), то елемнти a1; a2; : : : ; an називають аргументами функцi¨ f.
В загальному випадку вiдображення iз An â A назива¹ться n¡мiсною опера-
öi¹þ àáî n¡арною операцi¹ю. Бiнарнi операцi¨ звичайно називають додаванням,
множенням, комозицi¹ю та суперпозицi¹ю. Iншi назви використовують у випадках, коли операцiя введена в конкретнiй ситуацi¨ кимось давно i, вiдповiдно, давно введена кимось своя назва.
2.5 Вiдображення i послiдовностi
Кожне вiдображення f iз множини f1; 2; : : : ; ng у множину A можна задати послiдовнiстю пiдряд записаними значеннями вiдображення
(f(1):f(2); : : : ; f(n)) = (a1; a2; : : : ; an); f(i) = ai 2 A; 1 · i · n:
В зворотному напрямку кожну послiдовнiсть (a1; a2; : : : ; an) елементiв iз множини A можна розглядати як послiдовно записанi значення певного вiдображе-
ííÿ f : f1; 2; : : : ; ng ! A: Таким чином, виника¹ природна вза¹мно однозначна вiдповiднiсть мiж вiдображеннями f : f1; 2; : : : ; ng ! A i послiдовностями довжини n лементiв iз A. Звiдси виплива¹, що коли мiркування ведуться з точнiстю
до канонiчно¨ вза¹мно однозначно¨ вiдповiдностi, то послiдовнiстю називають
функцiю f : f1; 2; : : : ; ng ! A.
Подiбним чином, нескiнченнi послiдовностi a1; a2; : : : елементiв iз множини A це вiдображення iз N â A
9
3 Композицiя вiдображень та вiдношень.
3.1 Складна функцiя.
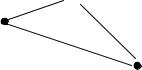
Нехай ма¹мо три множини A; B; C i два вiдображення f : A ! B, g : B ! C: Тодi можна побудувати вiдображення h : A ! C наступним чином. Беремо довiльний елемент a 2 A Шука¹мо елемент b 2 B, для якого f(a) = b. Далi шука¹мо елмент c 2 C такий, що g(b) = c: Далi за визначням, кажемо, що h(a) = c (див рис. 7). Щоб пiдкреслити, що функцiя h одержана за допомогою композицi¨ двох функцiй, кажуть, що h складна функцiя
Звернемо увагу на некомутативнiсть композицi¨ першою дi¹ та функцiя, те вiдображення, яке в добутку сто¨ть справа. Це зумовлене домовленiстю про запис аргумента справа вiд функцi¨.
Всi вiдображення iз задано¨ множини A задану множину B творюють множину, яка познача¹ться BA.
af 1  b = f(a)
b = f(a)
g
h
qR c = g(b) = h(a) = g(f(a))
Рис. 7: Дiя композицi¨ h = g ¢ f на елемент a.
f(x1; x2; : : : ; xn i функцiй
gi(y1; y2; : : : ; yk); i = 1; 2; : : : n: Суперпозицi¹ю буде нова функцiя h(y1; y2; : : : ; yk);
значення яко¨ обчислюються за правилом
h(y1; y2; : : : ; yk) = f(g1(y1; y2; : : : ; yk); g2(y1; y2; : : : ; yk); : : : gn(y1; y2; : : : ; yk))
.
3.2 Композицiя вiдношень.
Для бiнарних вiдношень P; Q
(a; b) 2 R
(a; b) 2 P
на множинi A визначена композицiя R = P ¢ Q :
, 9c((a; c) 2 P ^ (c; b) 2 Q): |
(5) |
P ¡1:
¡1 , ((b; a) 2 P ) ^ (c; b) 2 Q:
Розглянемо декiлька прикладiв.
10
