
- •Излучение сверхширокополосных сигналов
- •1. Введение
- •1.1. Определения
- •1.2. Области использования сшс
- •1.3. Излучатели несинусоидальных сигналов
- •1.4. Характеристики сшс
- •1.5. Характеристики излучателей
- •1.5.1.Диаграмма направленности и другие характеристики направленности
- •1.5.2.Коэффициент направленного действия
- •И наконец, эффективная изотропно излучаемая мощность (эиим) определяется как: .
- •2. Зоны излучения
- •2.1. Зоны излучения излучателей синусоидальных волн.
- •3.Волновые уравнения для потенциалов (метод векторного потенциала)
- •4. Энергетические соотношения для нестационарного поля
- •5. Принцип суперпозиции (интеграл Дюамеля)
- •6. Элементарные излучатели
- •6.1. Электрический диполь Герца
- •6.2. Магнитный диполь Герца
- •6.3. Излучатель Гюйгенса
- •(Метод модового базиса)
- •7.1. Постановка задачи
- •7.2. Представление трехмерных векторов
- •7.3. Исключение продольных компонент поля
- •7.4. Операторы ив пространстве
- •7.5. Доказательство самосопряженности операторов
- •7.6. Докажем, что векторы иортогональны:
- •7.10.2. Метод разделения переменных
- •Примеры решений задач
- •1. Излучение источника нестационарного тока с произвольным амплитудным распределением
- •2. Излучение нестационарных полей раскрывом коаксиального волновода с бесконечным фланцем
- •Самосопряженность
- •4. Теория линейных излучателей
- •4.1 Прямолинейный излучатель
- •4.2. Расчет распределения тока по излучателю.
- •4.3 Линейный излучатель с бегущей волной тока.
- •4.4. Излучатель произвольной формы.
- •3.2 Элементарный магнитный диполь.
- •3.3 Элементарная площадка.
(Метод модового базиса)
7.1. Постановка задачи
При помощи метода эволюционных уравнений можно свести исходную трехмерную нестационарную задачу излучения к одномерной нестационарной задаче, тем самым облегчив ее решение в силу уменьшения размерности, но не потеряв явную зависимость полей от времени. Это возможно благодаря тому, что в поперечной плоскости в цилиндрической системе координат будет построен базис, на который и будут спроектированы уравнения Максвелла. Тем самым мы избавимся от зависимостей уравнений от поперечных координат. Полученные одномерные уравнения называются эволюционными. В частном случае они сводятся к трем одномерным нестационарным уравнениям в частных производных.
Запишем Ссистемау уравнений Максвелла:

 ;
;

 ;
;

 ;
;

 ,
,
в которой для удобства трехмерные векторы обозначены жирным шрифтом. Она дополняется Мматериальныеми уравнениями:

 ;
;

 .
.
Следствием этих уравнений есть Ууравнение непрерывности

 .
.
Будем полагать,
что параметры среды могут зависеть от
продольной координаты и времени:
 ,
, .
Данная исходная задача дополняется
начальными (граничными) условиями для
полей и токов.
.
Данная исходная задача дополняется
начальными (граничными) условиями для
полей и токов.
7.2. Представление трехмерных векторов
Представим Ттрехмерные векторы в виде суммы и двумерныех и одномерных следующим образом векторы:

 ;
;

 ;
;

 ;
;

 .
.
 Используя
данные обозначения, представим
дивергентные
уравнения
Максвелла в следующем виде:
Используя
данные обозначения, представим
дивергентные
уравнения
Максвелла в следующем виде:
.

 ; (1)
; (1)

 . (2)
. (2)
Так как ротор произвольного вектора в выбранных обозначениях представляется в виде

 ,
,
причем первое слагаемое имеет только продольную составляющую, а второе и третье – поперечную, проекция роторных уравнений Максвелла на ось OZ представляется в виде
Роторные уравнения
Максвелла.

 ; (3)
; (3)
 , (4)
, (4)
а на поперечную плоскость –


 ; (5)
; (5)

 . (6)
. (6)
7.3. Исключение продольных компонент поля
Для построения базиса в поперечной плоскости исключим продольные компоненты поля из системы (1)-(6).
Исключим
ение

 из (5) при помощи (3) и (1), для чего подействуем
на левую и правую части выражения (5)
операцией
из (5) при помощи (3) и (1), для чего подействуем
на левую и правую части выражения (5)
операцией
 :
(5)
:
(5)
 ,
,
и в полученное выражение подставим соотношение (1), после чего имеем

 . (7)
. (7)
Для
использования выражения (3) необходимо
соотношение (5) записать в форме

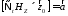 , умножить его векторно слева на
, умножить его векторно слева на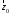 и применить известную формулу для
двойного векторного произведения
и применить известную формулу для
двойного векторного произведения
 ,
,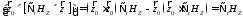
Ттогда (5) примет вид

 .
.  )
)
Подействовав на
последнее выражение операцией


 слева,
в полученное выражение
слева,
в полученное выражение
 можно подставить (3) и получить
можно подставить (3) и получить

 (8)
(8)
В результате (7) и (8) можно записать в виде
 ,
,
(9)
 ,
,
где
 ,
,
 .
.
Исключим

 из (6) при помощи (4) и (2), для чего подействуем
на левую и правую части выражения (6)
операцией
из (6) при помощи (4) и (2), для чего подействуем
на левую и правую части выражения (6)
операцией :
:
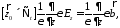
и
в полученное выражение подставим
соотношение (2), после чего имеем

 (10)
(10)
Для
использования выражения (4) необходимо
соотношение (6) записать в виде: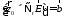 ,
умножить его векторно слева на
,
умножить его векторно слева на
 и применить известную формулу для
двойного векторного произведения
и применить известную формулу для
двойного векторного произведения
 ,
,
тогда (6) примет вид
 (
( )Подействовав
на последнее выражение операцией
)Подействовав
на последнее выражение операцией
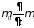

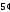 слева,
в полученное выражение
слева,
в полученное выражение
 можно подставить (4) и получить
можно подставить (4) и получить

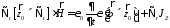 (
(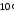 )
)
Обобщим
(10) и(11), записав в виде
 (12)
(12)
где

