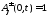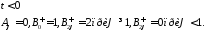- •Излучение сверхширокополосных сигналов
- •1. Введение
- •1.1. Определения
- •1.2. Области использования сшс
- •1.3. Излучатели несинусоидальных сигналов
- •1.4. Характеристики сшс
- •1.5. Характеристики излучателей
- •1.5.1.Диаграмма направленности и другие характеристики направленности
- •1.5.2.Коэффициент направленного действия
- •И наконец, эффективная изотропно излучаемая мощность (эиим) определяется как: .
- •2. Зоны излучения
- •2.1. Зоны излучения излучателей синусоидальных волн.
- •3.Волновые уравнения для потенциалов (метод векторного потенциала)
- •4. Энергетические соотношения для нестационарного поля
- •5. Принцип суперпозиции (интеграл Дюамеля)
- •6. Элементарные излучатели
- •6.1. Электрический диполь Герца
- •6.2. Магнитный диполь Герца
- •6.3. Излучатель Гюйгенса
- •(Метод модового базиса)
- •7.1. Постановка задачи
- •7.2. Представление трехмерных векторов
- •7.3. Исключение продольных компонент поля
- •7.4. Операторы ив пространстве
- •7.5. Доказательство самосопряженности операторов
- •7.6. Докажем, что векторы иортогональны:
- •7.10.2. Метод разделения переменных
- •Примеры решений задач
- •1. Излучение источника нестационарного тока с произвольным амплитудным распределением
- •2. Излучение нестационарных полей раскрывом коаксиального волновода с бесконечным фланцем
- •Самосопряженность
- •4. Теория линейных излучателей
- •4.1 Прямолинейный излучатель
- •4.2. Расчет распределения тока по излучателю.
- •4.3 Линейный излучатель с бегущей волной тока.
- •4.4. Излучатель произвольной формы.
- •3.2 Элементарный магнитный диполь.
- •3.3 Элементарная площадка.
7.4. Операторы ив пространстве
Применительно
к (10) и (12) введем две матричные
дифференциальные операции
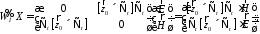
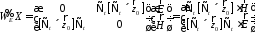
Введем энергетическую
метрику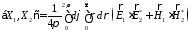
Наши новые операторы включают и матричные операции, и условие убывания поля на бесконечности:
 ;
; .
.
7.5. Доказательство самосопряженности операторов
Операторы
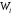 и
и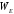 есть самосопряженные, если:
есть самосопряженные, если:
Для
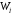 :
: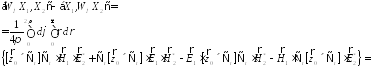

Выразим
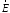 и
и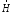 через производящую функцию
через производящую функцию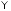 следующим образом:
следующим образом: ,
,
где
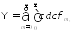
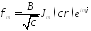
Таким образом
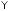 -произвольная
функция поперечных координат (используется
преобразование Фурье-Бесселя).
Подставим:
-произвольная
функция поперечных координат (используется
преобразование Фурье-Бесселя).
Подставим: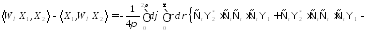
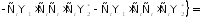


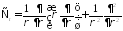
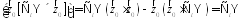


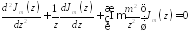

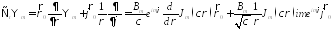
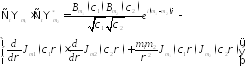
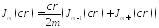
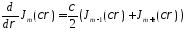
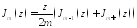

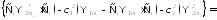
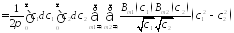

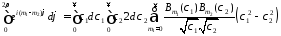
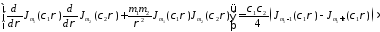
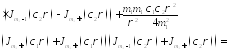
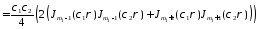

=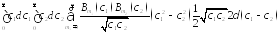 =
=
=
=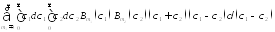 =
=
=
=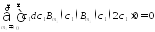
Докажем то же самое
для
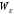 :
: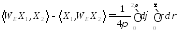

Докажем и для вектор-функций вида
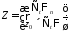 ,
,
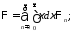
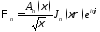
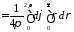


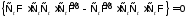
Доказательство – аналогично ранее представленному.
Собственные
векторы и собственные числа
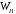 и
и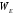
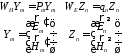
Подставим
определения операторов
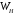 и
и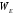 :
: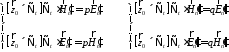 (13)
(13)
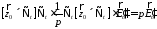

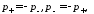 а
также
а
также
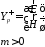 ,
,
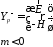
Определим
собственные векторы через производящие
функции:
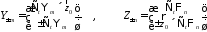 (14)
(14)
Подставим в (13) эти определения и получим 1)
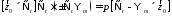
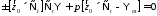
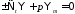 (15)
2)
(15)
2)
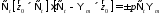
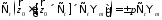
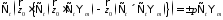

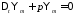 3)
3)
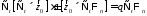
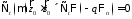
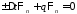 (16)
4)
(16)
4)
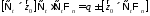




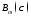 и
и
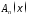 найдем из условий нормировки
найдем из условий нормировки
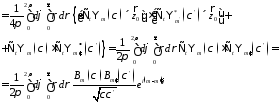

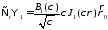
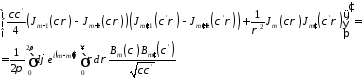
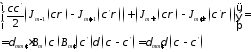
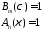
7.6. Докажем, что векторы иортогональны:


Прудников 1983 с.209 2.13.31
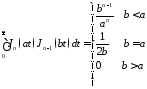
7.7.
Разложение произвольного вектора ЭМП
имеет вид
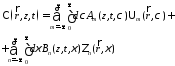 (17)
(17)
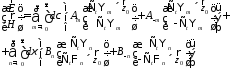
Введём
новые коэффициенты
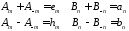 (18)
(18)
Разложения
поперечных компонент поля
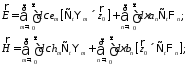 (19)
(19)

Подставим (19) в (3):
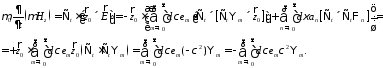 Значит
Значит
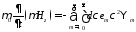 (20)
(20)
Подставим (19) в (1)
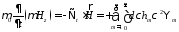 (21)
(21)
Подставим (10) в (4)
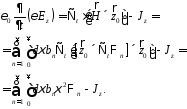 (22)
(22)
Подставим (19) в (2)
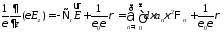 (23)
(23)
7.8. Проектирование уравнений Максвелла на базис
По аналогии с E- и H- волнами в свободном пространстве, введем разложение предельных компонент поля:

Подставим (24) в (20-23)

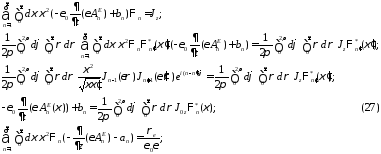 по
аналогии:
по
аналогии:
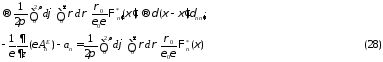 Подставим
разложения (19) и (24) в векторные уравнения
(5) и (6):
Подставим
разложения (19) и (24) в векторные уравнения
(5) и (6):
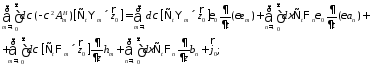
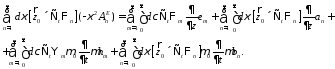
Отсюда, пользуясь ортогональностью мембранных функций, получим следующие уравнения:
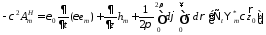
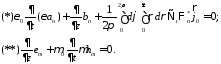
Подставим сюда (25-28):
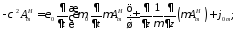

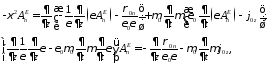
где
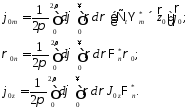
Докажем, что пара уравнений ((*),(**)) является следствием (25-28):
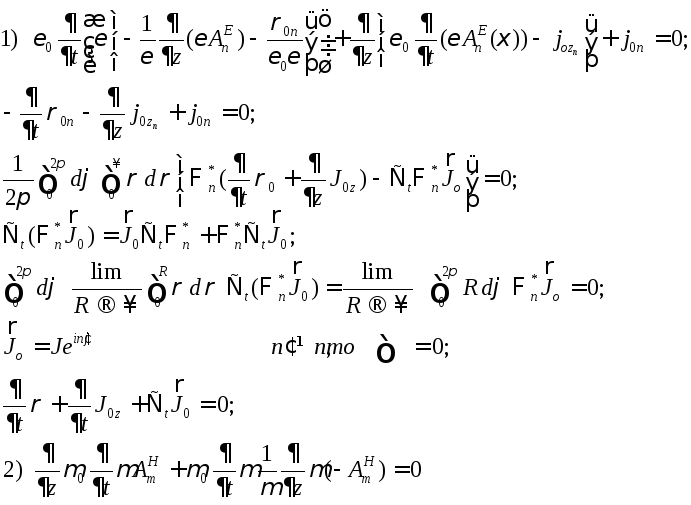
7.9. Система эволюционных уравнений
H-волны:

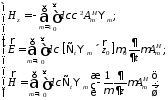

E-волны:
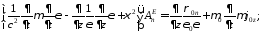
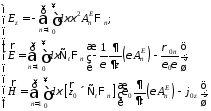
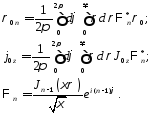
7.10. Методы решения эволюционных уравнений
7.10.1. Метод функции Римана
Для неоднородного уравнения типа Клейна-Гордона
 ,
,
описывающего эволюцию продольной составляющей компоненты поля соответствующей моды, возбужденной сторонним источником, вклад которого в данную моду задается функцией в правой части этого уравнения, существует решение:, полученное методом функции Римана
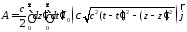 ,
,
в котором функция Бесселя есть решение для плоского источника тока или заряда с временной зависимостью в виде дельта-функции Дирака и с распределением в поперечной плоскости как у соответствующей моды.
Данный метод, отражающий принцип суперпозиции, можно применять, если нам известно пространственно-распределение стороннего источника.
7.10.2. Метод разделения переменных
Метод разделения
переменных (метод Фурье) применяется
для нахождения общего решения уравнения.
При этом источники задаются в начальных
(граничных) условиях для эволюционного
коэффициента. Суть этого метода состоит
в том, чтобы в исходном уравнении отделить
зависимости решения от одной и от другой
переменной, что дает возможность
представить решение в виде произведения
двух функций, каждая из которых зависит
только от одной переменной. После этого
для каждой из этих функций записывается
отдельное обыкновенное дифференциальное
уравнение
2) Метод разделения переменных.
Применение данного метода к уравнению
Клейна-Гордона дает обычное решение,
аналогичное применению преобразования
Фурье по времени. Но можно предварительно
произвести в данном уравнении замены
переменных, получить новое уравнение
в частных производных, которое также
можно решать методом Фурье. Методы
теории групп позволяют не только найти
все возможные замены переменных, но и
доказать, что других замен переменных,
приводящих к уравнению с разделяющимися
переменными, не существует. Такое
исследование уравнения Клейна-Гордона
было проведено в работе [Миллер У. мл.
Симметрия и разделение переменных. –
М.: Мир, 1981.– 342 c.]. Всего найдено десять
вариантов подстановок, при которых
переменные разделяются. В работе [Kalnins
E.G.
On
the
separation
variables
for
the
Laplace
equation
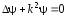 in
two
– and
three–dimensional
Minkowski
space
// SIAM
J.
Math.
Anal.
– 1975. – V.6,
N2.
– P.340–374.]
приводятся все варианты замен переменных
одномерного уравнения Клейна-Гордона
с подробным их анализом с точки зрения
покрытия решениями конуса Минковского.
Это вызвано тем, что не все подстановки
приводят к решениям, существующим для
всех необходимых
in
two
– and
three–dimensional
Minkowski
space
// SIAM
J.
Math.
Anal.
– 1975. – V.6,
N2.
– P.340–374.]
приводятся все варианты замен переменных
одномерного уравнения Клейна-Гордона
с подробным их анализом с точки зрения
покрытия решениями конуса Минковского.
Это вызвано тем, что не все подстановки
приводят к решениям, существующим для
всех необходимых
 и
и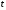 .
Первый простейший вариант замены
переменных приводит к решению в виде
экспонент, эквивалентному применению
преобразованию Фурье по временной
переменной, что фактически для нас
приводит к исчезновению причинно-следственных
связей в решении нестационарной задачи.
Наиболее интересна и перспективна с
точки зрения возможности получения
аналитических решений вторая замена
переменных:
.
Первый простейший вариант замены
переменных приводит к решению в виде
экспонент, эквивалентному применению
преобразованию Фурье по временной
переменной, что фактически для нас
приводит к исчезновению причинно-следственных
связей в решении нестационарной задачи.
Наиболее интересна и перспективна с
точки зрения возможности получения
аналитических решений вторая замена
переменных:
:
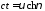 ;
;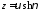 ,
,
или, наоборот,
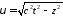 ;
;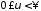 ;
;
 ;
; ,
,
 имея
ввиду известную формулу
имея
ввиду известную формулу ,
при
,
при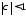 .
.
Производя данную
замену переменных в однородном уравнении
Клейна-Гордона
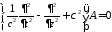 ,
получим новое уравнение
,
получим новое уравнение


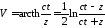
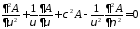
с разделяющимися
переменными, что легко проверить при
подстановке Если
 .
В результате, получим новое уравнение,
то
.
В результате, получим новое уравнение,
то
 ,
,
состоящее из двух слагаемых, зависящих только от своей переменной, и, согласно основной идее нахождения решения методом разделения переменных, мы будем полагать, что каждое слагаемое равняется какому-то числу:
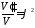 ;
;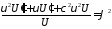 ,
,
где
 – любое число: натуральное, целое,
действительное, комплексное; при этом,
как легко видеть, исходное уравнение
удовлетворяется всегда. Полученные
соотношения приводят к замене одного
уравнения второго порядка в частных
производных на два обыкновенных
дифференциальных уравнения второго
порядка
– любое число: натуральное, целое,
действительное, комплексное; при этом,
как легко видеть, исходное уравнение
удовлетворяется всегда. Полученные
соотношения приводят к замене одного
уравнения второго порядка в частных
производных на два обыкновенных
дифференциальных уравнения второго
порядка
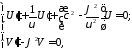
решения которых хорошо известны:
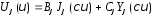 ;
;
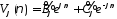 ,
,
где
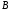 и
и – константы, подлежащие нахождению в
ходе решения соответствующих задач.
Подстановка данных решений в исходное
уравнение после возврата к старым
переменным дает общее решение уравнения
Клейна-Гордона
– константы, подлежащие нахождению в
ходе решения соответствующих задач.
Подстановка данных решений в исходное
уравнение после возврата к старым
переменным дает общее решение уравнения
Клейна-Гордона
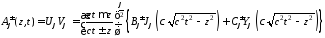 ,
,
удовлетворяющее
его при любых знаках, «+» или «–», при
любых константах
 и
и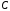 и при любых
и при любых .
.
Сравнивая общее
решение данного обобщенного волнового
уравнения с хорошо известным решением
обычного волнового уравнения в виде
запаздывающих и опережающих функций –
произвольных функций зависящих только
от аргумента
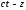 и
и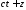 и описывающих волны, движущиеся слева
направо и справа налево соответственно,
можно сделать вывод, что данное решение
всегда состоит из волн, движущихся как
в одном, так и в другом направлении.
Выбор значений имеющихся констант
диктуется физическим смыслом и удобством
задания начальных (граничных) условий
и описывающих волны, движущиеся слева
направо и справа налево соответственно,
можно сделать вывод, что данное решение
всегда состоит из волн, движущихся как
в одном, так и в другом направлении.
Выбор значений имеющихся констант
диктуется физическим смыслом и удобством
задания начальных (граничных) условий
Используя
разложение
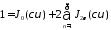 для
для