
- •Излучение сверхширокополосных сигналов
- •1. Введение
- •1.1. Определения
- •1.2. Области использования сшс
- •1.3. Излучатели несинусоидальных сигналов
- •1.4. Характеристики сшс
- •1.5. Характеристики излучателей
- •1.5.1.Диаграмма направленности и другие характеристики направленности
- •1.5.2.Коэффициент направленного действия
- •И наконец, эффективная изотропно излучаемая мощность (эиим) определяется как: .
- •2. Зоны излучения
- •2.1. Зоны излучения излучателей синусоидальных волн.
- •3.Волновые уравнения для потенциалов (метод векторного потенциала)
- •4. Энергетические соотношения для нестационарного поля
- •5. Принцип суперпозиции (интеграл Дюамеля)
- •6. Элементарные излучатели
- •6.1. Электрический диполь Герца
- •6.2. Магнитный диполь Герца
- •6.3. Излучатель Гюйгенса
- •(Метод модового базиса)
- •7.1. Постановка задачи
- •7.2. Представление трехмерных векторов
- •7.3. Исключение продольных компонент поля
- •7.4. Операторы ив пространстве
- •7.5. Доказательство самосопряженности операторов
- •7.6. Докажем, что векторы иортогональны:
- •7.10.2. Метод разделения переменных
- •Примеры решений задач
- •1. Излучение источника нестационарного тока с произвольным амплитудным распределением
- •2. Излучение нестационарных полей раскрывом коаксиального волновода с бесконечным фланцем
- •Самосопряженность
- •4. Теория линейных излучателей
- •4.1 Прямолинейный излучатель
- •4.2. Расчет распределения тока по излучателю.
- •4.3 Линейный излучатель с бегущей волной тока.
- •4.4. Излучатель произвольной формы.
- •3.2 Элементарный магнитный диполь.
- •3.3 Элементарная площадка.
6.3. Излучатель Гюйгенса
Рассмотрим излучение элементарной площадки с размерами много меньше пространственной длины импульса. Если эта площадка располагается на металлической поверхности, то при расчете считают, что поверхностные заряды отсутствуют, т.е. скалярный потенциал равен нулю, а расчет проводится по формуле
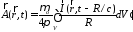 ,
,
где
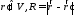 ,
в которой вместо объемного записывается
поверхностный интеграл и в силу малости
площадки имеет место,
,
в которой вместо объемного записывается
поверхностный интеграл и в силу малости
площадки имеет место,
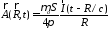 ,
,
где S – площадь площадки.
Если элементарная площадка, на которой задано распределение полей Е и Н, располагается в свободном пространстве, то такой излучатель называется излучателем Гюйгенса. Задача такого типа возникает при расчете рупорных и зеркальных антенн. Согласно принципу эквивалентных токов, на площадке S вводятся поверхностные электрические и магнитные токи
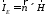 ,
,
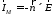 .
.
Рассматривается
суммарное поле, которое создается
электрическим диполем с током
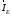 и повернутым относительно его на 90о
магнитным диполем с током
и повернутым относительно его на 90о
магнитным диполем с током
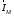 .
Угол поворота между между диполями
определяются углом между векторамиЕ
и Н
падающего поля. Геометрия задачи показана
на рисунке.
.
Угол поворота между между диполями
определяются углом между векторамиЕ
и Н
падающего поля. Геометрия задачи показана
на рисунке.
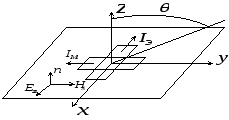
Для величин электрических и магнитных токов получены выражения с учетом того, значения токов будут пропорциональны длинам излучающей площадки:
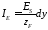 ,
,
где
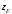 – волновое сопротивление фронта волны,
соотношение между амплитудами
электрической и магнитной компоненты
поля в плоскости излучателя, в свободном
пространстве
– волновое сопротивление фронта волны,
соотношение между амплитудами
электрической и магнитной компоненты
поля в плоскости излучателя, в свободном
пространстве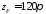 ,
,
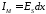 .
.
суммарное поле диполей для упрощения находится в трех различных плоскостях XOZ, YOZ.
Расчет поля в
плоскости XOZ
(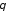 компонента) проводится следующим
образом: на основе полученных ранее
выражений в предыдущих системах координат
для поперечной компоненты поля,
излученного электрическим диполем
Герца
компонента) проводится следующим
образом: на основе полученных ранее
выражений в предыдущих системах координат
для поперечной компоненты поля,
излученного электрическим диполем
Герца
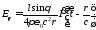
и магнитным
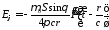 ,
,
с учетом только наиболее медленно убывающих слагаемых сложим вклады, вносимые этими диполями.
С учетом поворота на 90о относительно оси OY и пропорциональности поля длине участка тока dx электрическое поле электрического диполя приобретает вид
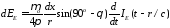
или, после упрощения, имеем
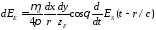 .
.
Составляющая
электрического поля магнитного диполя,
лежащая в плоскости XOZ,
не зависит от
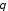 в выбранной системе координат, поэтому
в выбранной системе координат, поэтому
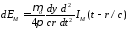 ,
,
а после упрощения
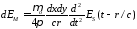 .
.
Поля диполей
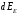 и
и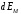 совпадают по направлению, поэтому могут
быть просуммированы. Для суммарного
поля двух диполей получаем
совпадают по направлению, поэтому могут
быть просуммированы. Для суммарного
поля двух диполей получаем
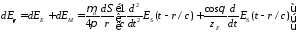 .
.
Поле Е
в плоскости YOZ
( компонента в выбранной системе координат)
определяются аналогично. В отличие от
предыдущих соотношений, составляющие
поля электрического и магнитного диполей
меняются угловой зависимостью
компонента в выбранной системе координат)
определяются аналогично. В отличие от
предыдущих соотношений, составляющие
поля электрического и магнитного диполей
меняются угловой зависимостью
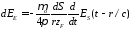 ;
;
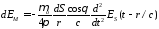 .
.
Суммарное поле имеет вид
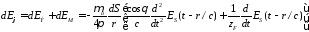
Поле
в любом направлении
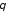 ,
, определяется как сумма векторов
определяется как сумма векторов
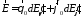 ,
,
где
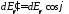 ,
,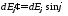 – проекции полей в выбранных плоскостях.
В итоге получим
– проекции полей в выбранных плоскостях.
В итоге получим
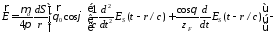
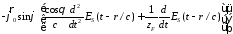 .
.
Учитывая, что рассчитывается излученное поле в дальней зоне, в которой магнитные компоненты связаны с электрическими посредством волнового сопротивления свободного пространства, можно записать магнитные компоненты следующим образом:
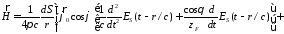
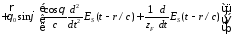 .
.
В заключение следует отметить, что временная форма и пространственное распределение излученного поля в дальней зоне зависит от временной зависимости возбуждающего поля.
7. Метод эволюционных уравнений
