
- •Излучение сверхширокополосных сигналов
- •1. Введение
- •1.1. Определения
- •1.2. Области использования сшс
- •1.3. Излучатели несинусоидальных сигналов
- •1.4. Характеристики сшс
- •1.5. Характеристики излучателей
- •1.5.1.Диаграмма направленности и другие характеристики направленности
- •1.5.2.Коэффициент направленного действия
- •И наконец, эффективная изотропно излучаемая мощность (эиим) определяется как: .
- •2. Зоны излучения
- •2.1. Зоны излучения излучателей синусоидальных волн.
- •3.Волновые уравнения для потенциалов (метод векторного потенциала)
- •4. Энергетические соотношения для нестационарного поля
- •5. Принцип суперпозиции (интеграл Дюамеля)
- •6. Элементарные излучатели
- •6.1. Электрический диполь Герца
- •6.2. Магнитный диполь Герца
- •6.3. Излучатель Гюйгенса
- •(Метод модового базиса)
- •7.1. Постановка задачи
- •7.2. Представление трехмерных векторов
- •7.3. Исключение продольных компонент поля
- •7.4. Операторы ив пространстве
- •7.5. Доказательство самосопряженности операторов
- •7.6. Докажем, что векторы иортогональны:
- •7.10.2. Метод разделения переменных
- •Примеры решений задач
- •1. Излучение источника нестационарного тока с произвольным амплитудным распределением
- •2. Излучение нестационарных полей раскрывом коаксиального волновода с бесконечным фланцем
- •Самосопряженность
- •4. Теория линейных излучателей
- •4.1 Прямолинейный излучатель
- •4.2. Расчет распределения тока по излучателю.
- •4.3 Линейный излучатель с бегущей волной тока.
- •4.4. Излучатель произвольной формы.
- •3.2 Элементарный магнитный диполь.
- •3.3 Элементарная площадка.
6.2. Магнитный диполь Герца
Моделью элементарного
магнитного излучателя может быть
бесконечно малая рамка с током (петля).

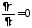
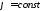

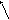
Для нее в силу
равенства входящего и выходящего тока
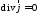 ,
тогда
,
тогда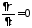 ,
следовательно, скалярный потенциал
,
следовательно, скалярный потенциал .
В силу этого представляет интерес только
векторный потенциал
.
В силу этого представляет интерес только
векторный потенциал
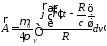 , (1)
, (1)
где

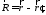

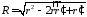 .
.
Если
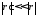
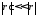 ,
то
,
то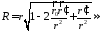
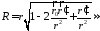
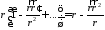
 ,
тогда
,
тогда
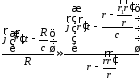
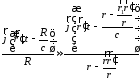 .
.
Пользуясь разложением
в ряд Тейлора с удержанием первых двух
слагаемых 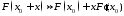
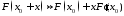 ,
если x
– мало,
для функции
,
если x
– мало,
для функции
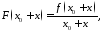
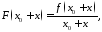 имеем
имеем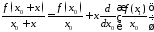
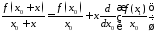 ,
где
,
где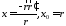
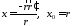 .
.
Тогда
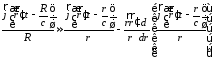
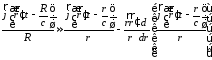 подставим в (1) и получим
подставим в (1) и получим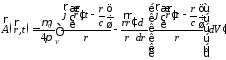
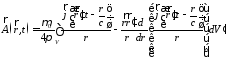 .
.
Расстояние до точки наблюдения r в знаменателе первого слагаемого можно вынести за знак интеграла и убедиться, что первое слагаемое дает нулевой вклад в потенциал в силу замкнутости токов. Обозначая производную по времени точкой, перепишем
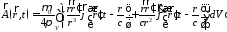 .
.
Проведем
некоторые векторные преобразования с
имеющимся вектором


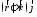 .
Так как
.
Так как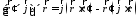 ,
то
,
то
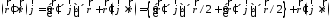 Заменим
второе слагаемое согласно вышеуказанной
формуле для двойного векторного
произведения и получим
Заменим
второе слагаемое согласно вышеуказанной
формуле для двойного векторного
произведения и получим
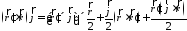 .
.
Подставляя
полученное преобразование в выражение
для векторного потенциала, с учетом
того, что вместо

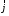 мы можем таким же образом подставить
мы можем таким же образом подставить
 ,
получим
,
получим

Докажем,
что в нашей
задаче вектор
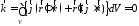
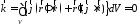 .
.
Домножим
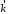
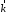 на произвольный вектор
на произвольный вектор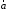
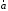
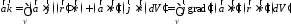
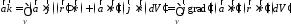 ,
,
где градиент
действует по штрихованным
координатам. Данное равенство легко
проверить, используя соотношение
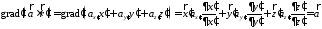
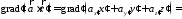
:
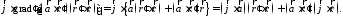
и
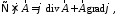
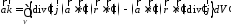
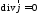
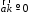
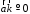
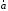
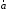
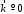
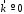
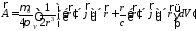
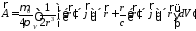
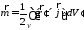
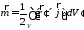
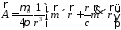
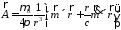
ак ак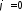
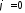

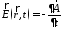 или после подстановки
или после подстановки
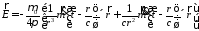
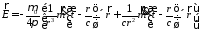 .
.
Если петля с током
лежит в плоскости XOY, то магнитный момент
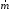
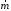 направлен вдоль оси OZ. Спроецируем
полученный вектор на орты сферической
системы координат:
направлен вдоль оси OZ. Спроецируем
полученный вектор на орты сферической
системы координат:
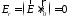
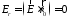 ;
;
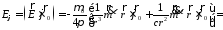
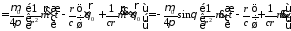 ;
;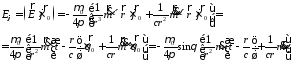
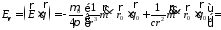

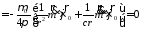 ;
;
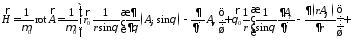

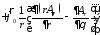 .
.
В силу осевой
симметрии задачи,
пренебрегая местом запитки петли, имеем
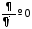
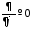 ,
и, учитывая, что
,
и, учитывая, что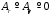
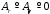 ,
в силу равенства нулю соответствующих
компонент электрического поля, полученного
выше, имеем
,
в силу равенства нулю соответствующих
компонент электрического поля, полученного
выше, имеем
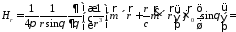
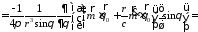
 ;
;


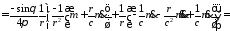
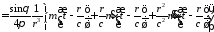 .
.
Рассмотрим петлю с током и рассчитаем для нее магнитный момент
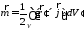
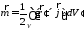 в двух системах
координат.
в двух системах
координат.
В цилиндрической системе координат:
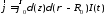
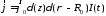 ,
,
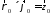
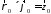 ,
,
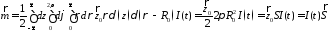
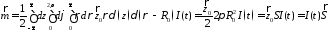 .
.
В сферической системе координат:
т.к.
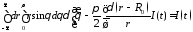
 ,
то
,
то
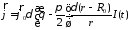
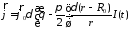 ,
,
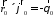
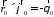 ,
,
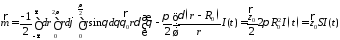
 Подставляя
полученный магнитный момент петли,
имеем
Подставляя
полученный магнитный момент петли,
имеем
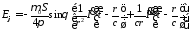
 ;
;

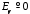 ;
;
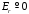
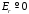 ;
;

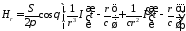 ;
;
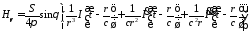
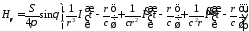 .
.
Видно, что волна с наименьшим убыванием в пространстве имеет временную зависимость в виде второй производной от возбуждающего тока. Квазистатическая составляющая убывает обратно пропорционально кубу расстояния, и ее временная зависимость совпадает с временной зависимостью тока. Как и в предыдущем случае, продольная компонента поля убывает быстрее поперечных.
Задача
Рассмотрим область
вокруг магнитного диполя, начиная со
сферы с произвольным радиусом
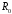
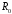 до сферы с радиусом
до сферы с радиусом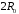
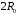 .
Проверим баланс энергии различных
составляющих поля для этой области.
.
Проверим баланс энергии различных
составляющих поля для этой области.
Найдем энергию квазистатической составляющей для импульса тока в виде скачка тока в момент времени, когда переходные процессы закончатся (постоянный ток):
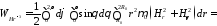
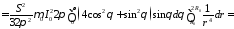

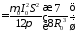 .
.
Пусть возбуждающий
импульс имеет линейно нарастающий фронт
длительности
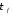
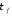 ,
,

но энергия квазистатической магнитной компоненты не зависит от характера нарастания, так как рассчитывалась при больших временах, когда ток можно считать практически постоянным
 .
.
Эта энергия
порождается всеми комбинациями компонент
электрического и магнитного поля в
рассматриваемой области, пока фронт
импульса растет. Входящую и выходящую
энергию рассчитаем посредством вектора
Пойнтинга. Напомним, что энергия есть
нелинейная характеристика поля. Учитывая,
что для выбранной временной зависимости
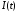 ,
,
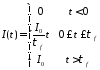 ,
,
 ,
,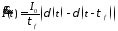 .
.
Вычислим разность входящей и выходящей энергии
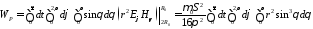
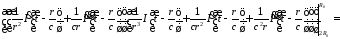
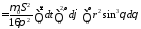
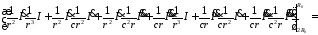

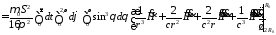 .
.
Так как последнее слагаемое не зависит от расстояния, то оно дает энергию на входе и на выходе одинаковую, это и есть энергия волны в дальней зоне. А у остальных слагаемых разность входящей и выходящей энергии будет не равна нулю, из них и будет составляться энергия постоянного магнитного поля вокруг излучателя. Рассчитаем вклад остальных слагаемых:
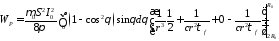 ,
,
интересно, что на этом этапе видно, что вклад в остаточную энергию дают наиболее быстро убывающие слагаемые в выражениях для поперечных компонент, из которых происхождение квазистатической магнитной компоненты понятно и следует из закона Ампера,
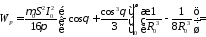
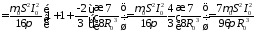 .
.
Как видно, закон сохранения энергии выполняется, энергия постоянного магнитного поля равняется энергии, вносимой нестационарной волной, причем в данном случае вклад определяется только квазистатической компонентой поперечного магнитного поля и первым слагаемым поперечного электрического поля. Отсюда можно сделать вывод, что без быстро убывающих с расстоянием слагаемых нельзя описать процесс наполнения пространства электромагнитной энергией. По крайней мере, очевидно, что все компоненты полей с разным затуханием в пространстве и временной зависимостью важны и имеют между собой неразрывную связь, которую можно назвать энергетической, так как без нее невозможно выполнение закона сохранения энергии в сложном процессе излучения распространяющейся волны.
