Лабораторная работа Определение величины земного ускорения при помощи машины Атвуда

Цель работы: измерить величину ускорения свободного падения при помощи машины Атвуда.

Краткая теория

Ускорение свободного падения g можно найти при помощи очень простого опыта: бросить тело с высоты h и измерить время падения t. Тогда g=2h/t². В действительности дело обстоит не так просто, если величину g требуется определить достаточно точно. Рассчитаем время падения t с высоты h=1,0м при g=9,8м/с²

При измерении такого промежутка времени с погрешностью t=0.01c относительная погрешность определения g, равная, будет более 4.5% и абсолютная погрешность g>0.5m/c². Казалось бы, чтобы снизить погрешность определения g, используя секундомер с той же погрешностью t=0.01c, надо увеличить измеряемый промежуток времени, увеличивая высоту падения. Так при h=5м время падения около 1с, а при h=20м - t2c. Однако в этом случае возникают ошибки другого характера.

Дело в том, что при больших скоростях заметную роль играет сопротивление воздуха, а формула равноускоренного движения h=gt²/2 этого фактора не учитывает. Таким образом, увеличивая высоту h, мы увеличиваем время падения и уменьшаем относительную погрешность его измерения, но при этом вносим другую ошибку: сама формула h=gt²/2 становится неточной. Например, если сбросить кирпич с высоты h=500м, то около 200м он будет двигаться с ускорением, а затем сила сопротивления воздуха станет равна силе тяжести (это будет при скорости 70 м/с) и тело остальные 300м будет двигаться с постоянной скоростью.

Приведенный простой пример наглядно демонстрирует общую черту любого физического эксперимента. В любом эксперименте точность определения какой-либо физической величины связана не только с точностью измерительных приборов, но и с тем насколько точно принятая модель описывает данный опыт, иначе говоря, насколько модель адекватна экспериментальной ситуации. Очевидно, что при обработке экспериментальных данных по формулам приближенной модели полученные результаты будут отличаться от истинного значения измеряемой величины. Это отличие имеет смысл систематической погрешности. Для ее учета надо строить более точную модель эксперимента.

Итак, сложности такого внешне простого опыта связаны с большим ускорением тела, за которым мы следим во время опыта. Так как ускорение большое, то тело быстро набирает скорость, а при этом или время движения мало и его трудно измерить, или сама формула равноускоренного движения неточна.

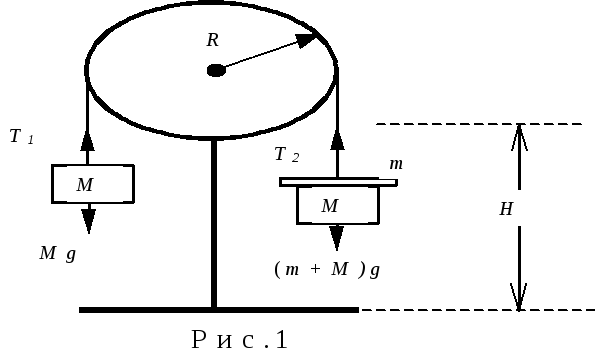
Уменьшить ускорение можно с помощью устройства, которое называется машиной Атвуда (рис.1). Через блок перекинута нить, на которой укреплены грузы с массой M каждый. На один из грузов накладывается перегрузок с массой m. Система начнет двигаться с ускорением a. Пройдя расстояние S-H, перегрузок m снимается. Система продолжает двигаться по инерции, проходя путь H.

Время прохождения этого расстояния можно точно измерить. Для достижения цели - как можно более точного для наших условий определения ускорения свободного падения g - необходимо построить модель экспериментальной ситуации, которая реализуется в машине Атвуда. В рамках этой модели надо найти связь между t и H и указать метод определения из такой зависимости интересующей нас величины g.

Н

аиболее простая модель нашей экспериментальной установки такова: блок и нить невесомы (их массы равны нулю), нить нерастяжима; трением в блоке и сопротивлением воздуха пренебречь. Тогда уравнения движения грузов имеют следующий вид

. (1)

Здесь T - сила натяжения нитей (при сделанных предположениях эти силы одинаковы), a - ускорение грузов. Решая систему (1), получаем

. (2)

Из этой формулы видно, что система будет двигаться с постоянным ускорением, причем a=0, если m=0 (то есть система будет двигаться равномерно при снятом перегрузке). До снятия перегрузка система пройдет расстояние S-H и, к моменту снятия перегрузка, она будет иметь скорость, которую можно рассчитать по формуле v²=2a(S-H). Скорость v можно экспериментально определить, измерив время t прохождения системой пути H. Итак, получаем связь между t и H

. (3)

Таким образом, определив экспериментально зависимость t от H, по формуле (3) можно найти величину a (это можно сделать методом наименьших квадратов) и далее по формуле (2), используя известные значения m и M, рассчитать ускорение свободного падения g.

Рассмотрим более реалистичную модель машины Атвуда. В этой модели учтем то, что масса блока не равна нулю. Теперь необходимо считать, что система состоит из трех тел - двух грузов с массами M и M+m, и блока, имеющего момент инерции J. Для описания движения такой системы к уравнениям движения грузов надо добавить уравнение движения для блока (уравнение моментов). Обратим внимание на тот факт, что в рассматриваемой модели силы натяжения нити, действующие на грузы, неравны. Имеем

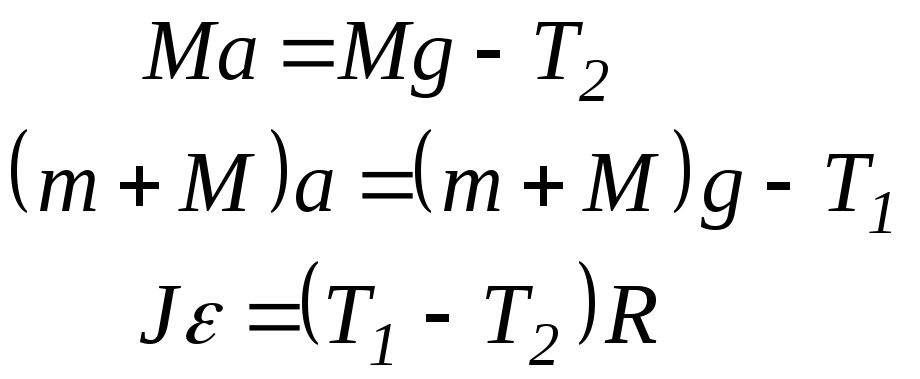. (4)

Последнее уравнение - это уравнение моментов. Здесь  - угловое ускорение, которое в отсутствие проскальзывания нити по блоку равно =a/R, где R - радиус блока. Решая эту систему, получаем

. (5)

Из этой формулы видно, что при J=0 она переходит в выражение (2). Так же, как и раньше, в отсутствии перегрузка, то есть при m=0, ускорение a равно нулю. Значит, расстояние H система будет проходить с постоянной скоростью и связь между H и t такая же, как и первой модели. Способы обработки результатов эксперимента практически не отличаются от используемых в первой модели. Как и раньше из экспериментальной зависимости t от H методом наименьших квадратов можно найти a, но ускорение свободного падения теперь вычисляется при помощи выражения (5).

В формуле (5) неизвестна величина момента инерции блока J относительно оси вращения. Оценить величину J можно, если считать блок диском радиусом R и массой m_Б, в котором вырезаны отверстия радиусом r, а центры этих отверстий находятся на расстоянии l от центра вращения. Вывод выражения для J такой модели блока приведен в приложении, где также приведена оценка величины момента инерции блока, которая составила J95гcм². На самом деле блок представляет более сложную конструкцию, которая включает в себя не только фигурный диск, но и ось, которая закреплена в подшипниках. Рассчитать момент инерции такой конструкции в принципе можно, но эти вычисления достаточно громоздки, поэтому значение J гораздо проще измерить, например, так, как это делается в лабораторной работе №4. Такое измерение дает J=(94,70.5)гcм².

Теперь нетрудно оценить погрешность определения g, которую мы бы допустили, если пользовались результатами первой модели. Так в нашей установке величина 2M+m равна приблизительно 125г, величина R4cм и, значит, I/R²6г. Таким образом, пренебрежение моментом инерции блока приводит к уменьшению знаменателя в формуле (2) примерно на 5% и, как следствие, к такому же примерно завышению g, определенного по формулам первой модели.

Завершая обсуждение второй модели, сделаем еще следующее замечание. Формуле (5) можно придать более простой вид, аналогичный выражению (2), если ввести новую величину , которая характеризует инерционные свойства системы, обусловленные не только массами грузов, но и инерционными свойствами блока, поэтому величину M₀ можно назвать эквивалентной массой груза. Используя эту величину, формула (5) преобразуется к виду

. (6)

Этим выражением мы будем пользоваться в дальнейшем при обработке эксперимента.

Итак, вторая модель позволила нам учесть массу блока. Пренебрежение массой нити является хорошим приближением для данной установки, и его обсуждать мы не будем. Рассмотрим теперь приближения, связанные с силами трения. Силу трения грузов о воздух с хорошей точностью можно считать пропорциональной скорости их движения, то есть чем меньше скорость движения грузов, тем меньше сила сопротивления его движению и тем точнее выполняется приближение об отсутствии трения о воздух.

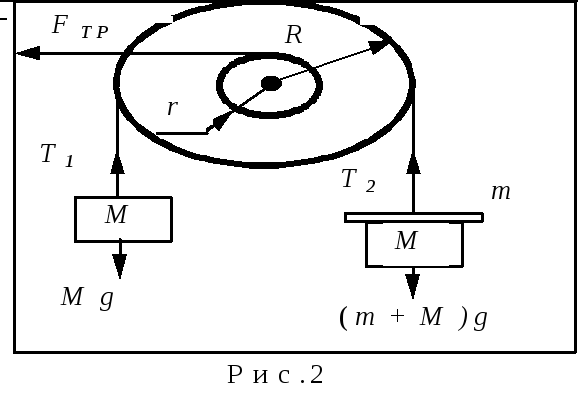
Казалось бы, в данной установке скорость движения грузов можно сделать как угодно малой. Формально это следует как из формулы (2), так и из формулы (5) - при m0 ускорение а0. Например, если M=5кг и m=1г, то m/2M=10^-4 и при опускании груза с высоты примерно 0,5 м его скорость не превысит величины 1мм/с. Однако реально такой опыт невыполним (система может даже не начать двигаться при наложении перегрузка). Дело в том, что в выбранных моделях мы предположили отсутствие трения в оси блока. В действительности оно есть и для учета его влияния на поведение системы нам надо снова уточнить модель, включив в нее силы трения, действующие в оси блока.

Уравнения движения с учетом силы трения в оси блока будут иметь следующий вид

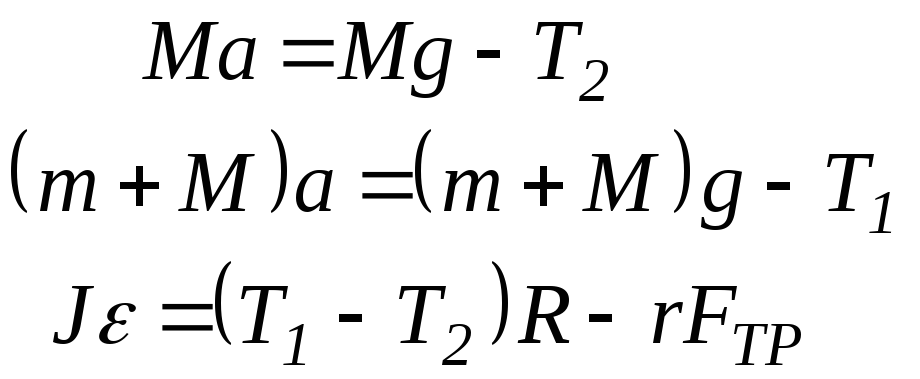. (7)

Здесь F_ТР - сила трения между блоком и осью, r - радиус оси (рис.2). Сила трения F_ТР прямопропорциональна силе давления на ось блока N, то есть F_ТР=N=(T₁+T₂), где  - коэффициент трения между блоком и осью, зависящий от свойств соприкасающихся поверхностей втулки блока и оси, состояния смазки и т.п.

Используя это соотношение и вспоминая также, что угловое ускорение блока связано с линейным ускорением по формуле =a/R, последнее уравнение системы (7) можно записать в следующем виде

Подставив в него T₁ и T₂, выраженные из первых двух уравнений системы (7), получаем

Используя величину М₀ и введя обозначение k=(r/R), выражение для ускорения системы можно представить в следующем виде

. (8)

Рассмотрим характер движения системы в зависимости от массы перегрузка. Если система в начальный момент времени находится в покое, то при постепенном увеличении массы перегрузка система будет продолжать оставаться в покое до тех пор пока наложенная масса не превысит некого значения m₀, которое легко определить из условия равенства нулю числителя в выражении (8).

. (9)

При m>m₀ система будет двигаться с ускорением, определяемым согласно формуле (8). В момент снятия перегрузка система будет обладать скоростью v=2a(S-H) и начнет двигаться равнозамедленно, то есть с отрицательным ускорением a₀, которое нетрудно вычислить, если в формуле (8) положить m=0

. (10)

Чтобы использовать результаты точной модели для определения ускорения свободного падения g по экспериментальным данным, полученным на машине Атвуда, надо уметь определять величину k, характеризующую силу трения в оси. Оценить величину k можно просто по формуле (9), зная m₀ - k=m₀ /(m₀+2M). По своему смыслу m₀ - это масса перегрузка, который только-только страгивает блок с грузами. Из-за этого "только-только" величина m₀ оценивается очень грубо. Например, перегрузок массой 1г не страгивает блока, а перегрузок массой 2г приводит блок в движение. Такое измерение позволяет заключить только, что 1г<m₀<2г. Это, очевидно, очень грубое оценочное измерение. Оно не может нас удовлетворить и вот по какой причине. Дело в том, что, как отмечалось выше, для надежного пренебрежения силой сопротивления воздуха необходимо, чтобы грузы двигались медленно, то есть ускорение a было мало. Как следует из формулы (8) и (9) это возможно, если масса перегрузка m незначительно превышает m₀. В этом случае, как можно показать, погрешность g существенным образом определяется погрешностью m₀, которая велика.

Существует другой метод определения k, использующий только экспериментальные результаты, полученные на машине Атвуда. То, что этот метод не требует дополнительных экспериментов, делает его особенно привлекательным, но за это приходится расплачиваться более сложными формулами для обработки эксперимента. Выведем эти формулы.

Для начала получим выражение для времени падения груза с высоты H. После прохождения участка S-H с ускорением a груз приобретает скорость v=2a(S-H). В этот момент начинается равнозамедленное движение с ускорением a₀. Время перемещения t и расстояние H связаны при этом известным соотношением

, (11)

где обозначения A=2a и B=a₀/2 введены для удобства.

В этой формуле S - известная величина, H и t измеряются экспериментально, значения же a и a₀, или, что то же самое, A и B подлежат определению. Вычислить эти величины методом наименьших квадратов, используя формулу (11) нельзя, так как эта формула задает неявную связь между измеряемыми величинами.

Как применять метод наименьших квадратов для нахождения A и B будет подробно изложено ниже. Сейчас же будем считать, что значения параметров A и B нам известны и выведем уравнение для расчета величины g. Выпишем выражения для A и B, используя формулы (8) и (10).

. (12)

Соотношения (12) представляют собой систему уравнений относительно неизвестных g и k. Выразив k из второго соотношения (k=-2BM₀/gM) и подставив его в первое, получим квадратное уравнение для величины g.

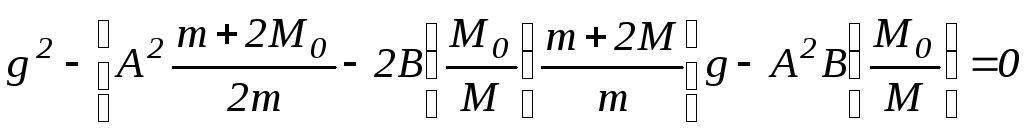. (13)

В этом уравнении все коэффициенты легко рассчитываются, зная параметры A и B, найденные из эксперимента, и параметры установки m, M и M₀. Нетрудно рассчитать также и погрешности этих коэффициентов. Далее, найдя корни этого уравнения и выбрав из них физически разумный, можно вычислить величину ускорения свободного падения.

Таким образом, мы рассмотрели результаты трех моделей, описывающих движение машины Атвуда. Последняя модель наиболее полно, по сравнению с предыдущими, учитывает детали движения грузов. Можно, конечно, и далее совершенствовать модель, включая в нее другие тела и другие силы, оказывающие влияние на движение системы. Например, можно учесть влияние на характер движения массы нити. Но надо ли это? Ведь интуитивно мы понимаем, что учет массы нити даст поправку к значению g, не превышающую отношения массы нити к эффективной массе системы. Но это отношение можно сделать как угодно малым, увеличивая массу M.

Можно было бы уточнять модель, вводя в рассмотрение силу сопротивления воздуха, действующую на грузы при их движении. Но это приводит к значительным математическим сложностям. По этой причине может оказаться более простым проведение экспериментов с машиной Атвуда в вакууме.

Процесс совершенствования физической модели реального объекта бесконечен. Стоит вопрос о том, что надо где-то остановиться, чем-то ограничится. Указание на такую границу может дать точность эксперимента, поскольку очевидно, что если уточнение модели дает поправку меньшую, чем точность эксперимента, то такое усовершенствование бесполезно

Стимулом для дальнейшего совершенствования, уточнения или изменения модели служат, в первую очередь, выводы следующие из эксперимента, сделанные на основании той или иной модели. Так, например, для нашего случая при обработке результатов эксперимента по формулам первой модели получается, что величина g зависит от массы перегрузка m. Этот факт противоречит принципу эквивалентности инертной и гравитационной массы, справедливость которого установлена с высокой точностью. Отсюда следует вывод о неполноте модели нашей установки и необходимости ее уточнения.

Можно привести пример другого рода. Точные измерение земного ускорения, проведенные на разных географических широтах, дают разные его значения. Ускорение тем меньше, чем меньше широта (на экваторе величина земного ускорения наименьшая). Эта зависимость, очевидно, обусловлена вращением Земли и указывает на необходимость учитывать в физической модели эксперимента это вращение, например, путем введения центробежной силы.